2024 AMC 12A Problems/Problem 10

Problem

Let $\alpha$ be the radian measure of the smallest angle in a $3{-}4{-}5$ right triangle. Let $\beta$ be the radian measure of the smallest angle in a $7{-}24{-}25$ right triangle. In terms of $\alpha$ , what is $\beta$ ?

$\textbf{(A) }\frac{\alpha}{3}\qquad \textbf{(B) }\alpha - \frac{\pi}{8}\qquad \textbf{(C) }\frac{\pi}{2} - 2\alpha \qquad \textbf{(D) }\frac{\alpha}{2}\qquad \textbf{(E) }\pi - 4\alpha\qquad$

Solution 1

From the question, $\tan\alpha=\frac{3}{4}, \space \tan\beta=\frac{7}{24}$ $\tan(\alpha+\beta)= \frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}$ $\tan(\alpha+\beta)= \frac{\frac{3}{4}+\frac{7}{24}}{1-\frac{3}{4} \cdot \frac{7}{24}}$ $\tan(\alpha+\beta)=\frac{4}{3}$ $\alpha+\beta=\tan^{-1}\left(\frac{4}{3}\right)$ $\alpha+\beta=\frac{\pi}{2}-\alpha$ $\beta=\boxed{\textbf{(C) }\frac{\pi}{2}-2\alpha}$

~lptoggled

Solution 2: Trial and Error

Another approach to solving this problem is trial and error, comparing the sine of the answer choices with $\sin\beta = \frac{7}{25}$ . Starting with the easiest sine to compute from the answer choices (option choice D). We get: $\sin{\left(\frac{\alpha}{2}\right)} = \sqrt{\frac{1 - \cos{\alpha}}{2}}$ $= \sqrt{\frac{1 - \frac{4}{5}}{2}}$ $= \sqrt{\frac{1}{10}}$ $\neq \frac{7}{25}$

The next easiest sine to compute is option choice C. $\sin{\left(\frac{\pi}{2} - 2\alpha\right)} = \sin{\left(\frac{\pi}{2}\right)}\cos{\left(2\alpha\right)}$ $=\cos{2\alpha}$ $=\cos^2{\alpha} - \sin^2{\alpha}$ $=\frac{16}{25} - \frac{9}{25}$ $=\frac{7}{25}$

Since $\sin\left(\frac{\pi}{2} - 2\alpha\right)$ is equal to $\sin\beta$ , option choice C is the correct answer. ~amshah

Solution 3:

sin(B) = $\frac{24}{25}$ = 2 * $\frac{12}{25}$ = 2 * $\frac{3}{5}$ * $\frac{4}{5}$ = 2 * sin(A) * cos(A) = Sin(2A) = Cos(90 - 2A)

choice C is the correct answer ~luckuso

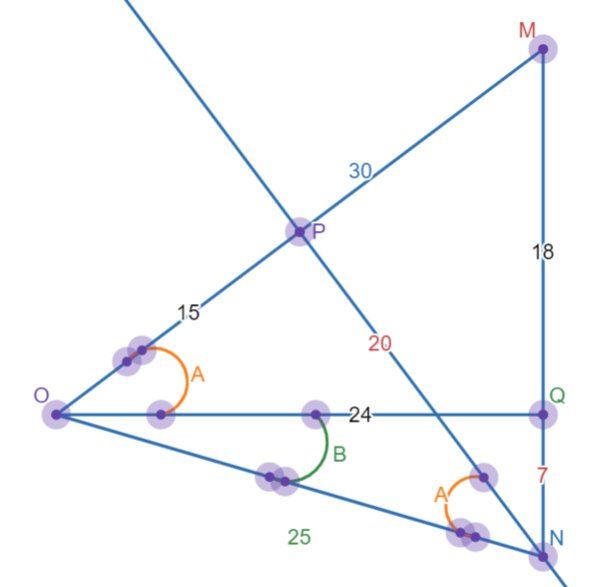
Solution 4: Ptolemy (no trig)

Let AB have length 15, BC have length 20, AC length 25, AD length 7 and CD length 24. Let x be the measure of segment BD. Thus the measure of angle ACB is $\alpha$ and the measure of angle ACD is $\beta$ . ABCD is a cyclic quadrilateral because angle ABC and angle ADC are right angles. Using Ptolemy's theorem on this quadrilateral yields 25x = 15*24 + 7*20 = 500, or x = 20. This means triangle CBD is isoceles. The perpendicular bisector of CD passes through the center (O) of the circle on which ABCD lies and also passes through B. Let the intersection of the perpendicular bisector of CD and CD be point P. The measure of angle OBC is the same as the measure of the angle OCB which is $\alpha$ , so the measure of angle BOC is ${\pi} - {2}{\alpha}$ , so the measure of angle COP is ${2}{\alpha}$ . Triangle COP is a right triangle with angle OCP being the same as angle ACD ( $\beta$ ), angle COP being ${2}{\alpha}$ , and angle CPO being $\frac{\pi}{2}$ . So: $\beta + {2}\alpha + \frac{\pi}{2} = \pi$ $\beta=\boxed{(C) \frac{\pi}{2} -2\alpha}$ ~Ilaggo2432

Solution 5(rough value)

given in the question,sin(a)is 3/5 and sin (b) is 7/25,estimate the angle by using the arcsin function. arcsin 3/5 is around 0.643 rad and arcsin 7/25 is around 0.283. Note that pi/2 is closest to 1.57 rad, try one by one and option c suggests that 1.57=2(0.643)+0.283. My first amc 12 edit

Solution 6 (Angle Addition)

$\sin(\alpha)\cos(\beta) + \sin(\beta)\cos(\alpha) = \sin(\alpha+\beta) = \frac{4}{5}$ . Noticing $\frac{4}{5} = \cos(\alpha) = \sin\left(\frac{\pi}{2}-\alpha\right)$ gives us $\alpha + \beta = \frac{\pi}{2} - \alpha$ so $\boxed{\textbf{(C) }\dfrac{\pi}{2} - 2\alpha}$ ~KEVIN_LIU

Solution 7 (Geometry Solution Without Words)

$\angle A+ \angle B+ \angle A = \frac{\pi}{2}$ ~luckuso

Solution 8 (Complex Number)

4 + 3i =

$25e^{i2A} = (4+3i)^2 = 16 + 9 * i^2 + 2*12 * i= 16- 9 + 24i = 7+ 24i$

24 + 7i = $25e^{iB}$

$\angle 2A+ \angle B = \frac{\pi}{2}$

~luckuso

Solution 9 (Co-function Identities)

$\cos(\alpha) = \frac{4}{5} \quad and \quad \sin(\alpha) = \frac{3}{5}$ $\cos(2\alpha) = \cos^2(\alpha) - \sin^2(\alpha) = \left(\frac{4}{5}\right)^2 - \left(\frac{3}{5}\right)^2 = \frac{16}{25} - \frac{9}{25} = \frac{7}{25}$ We know that $\sin(\beta) = \frac{7}{25}$ Equate both to each other $\cos(2\alpha) = \sin(\beta)$

Apply the cofunction identity, $\cos(\alpha) = \sin\left(\frac{\pi}{2} - \alpha\right)$ ,

$\sin\left(\frac{\pi}{2} - 2\alpha\right) = \sin(\beta)$

Hence, $\beta=\boxed{(\mathbf{C}) \frac{\pi}{2} - 2\alpha}$ ~sourodeepdeb

2024 AMC 12A (Problems • Answer Key • Resources)
Preceded by Problem 9	Followed by Problem 11
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

Page

Toolbox

Search