Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Kimberling’s point X(24)"
(→‎Theorem 3)
 
(11 intermediate revisions by the same user not shown)
Line 1: Line 1:
−
<i><b> Kimberling point X(24) </b></i>
+
== Kimberling's point X(24) ==
 
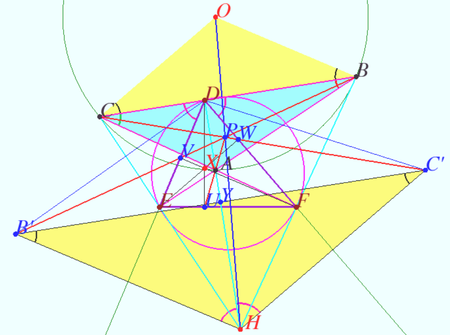
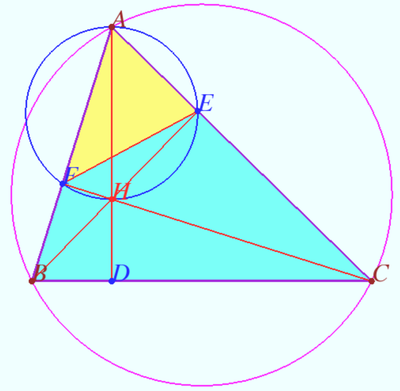
[[File:2016 USAMO 3g.png|450px|right]]
 
[[File:2016 USAMO 3g.png|450px|right]]
  
−
Perspector of Triangle <math>ABC</math> and Orthic Triangle of the Orthic Triangle.
+
Kimberling defined point X(24) as perspector of <math>\triangle ABC</math> and Orthic Triangle of the Orthic Triangle of <math>\triangle ABC</math>.
−
<i><b>Theorem 1</b></i>
+
 
−
Denote <math>T_0</math> obtuse or acute <math>\triangle ABC.</math> Let <math>T_0</math> be the base triangle, <math>T_1 = \triangle DEF</math> be Orthic triangle of <math>T_0, T_2 = \triangle UVW</math> be Orthic Triangle of the Orthic Triangle of <math>T_0</math>. Let <math>O</math> and <math>H</math> be the circumcenter and orthocenter of <math>T_0.</math>  
+
==Theorem 1==
 +
 
 +
Denote <math>T_0</math> obtuse or acute <math>\triangle ABC.</math> Let <math>T_0</math> be the base triangle, <math>T_1 = \triangle DEF</math> be Orthic triangle of <math>T_0, T_2 = \triangle UVW</math> be Orthic Triangle of <math>T_1</math>. Let <math>O</math> and <math>H</math> be the circumcenter and orthocenter of <math>T_0.</math>  
  
 
Then <math>\triangle T_0</math> and <math>\triangle T_2</math> are homothetic, the point <math>P,</math> center of this homothety lies on Euler line <math>OH</math> of <math>T_0.</math>  
 
Then <math>\triangle T_0</math> and <math>\triangle T_2</math> are homothetic, the point <math>P,</math> center of this homothety lies on Euler line <math>OH</math> of <math>T_0.</math>  
Line 13: Line 15:
  
 
WLOG, we use case <math>\angle A = \alpha > 90^\circ.</math>
 
WLOG, we use case <math>\angle A = \alpha > 90^\circ.</math>
−
Let <math>B'</math> be reflection <math>H</math> in <math>DE.</math>
 
  
−
In accordance with Claim, <math>\angle BVD = \angle HVE \implies B', V,</math> and <math>B</math> are collinear.
+
Let <math>B'</math> be reflection <math>H</math> in <math>DE.</math> In accordance with Claim, <math>\angle BVD = \angle HVE \implies B', V,</math> and <math>B</math> are collinear.
  
 
Similarly, <math>C, W,</math> and <math>C',</math> were <math>C'</math> is reflection <math>H</math> in <math>DF,</math> are collinear.
 
Similarly, <math>C, W,</math> and <math>C',</math> were <math>C'</math> is reflection <math>H</math> in <math>DF,</math> are collinear.
Line 28: Line 29:
 
<math>\triangle HB'C' \sim \triangle OBC, BB', CC'</math> and <math>HO</math> are concurrent at point <math>P.</math>
 
<math>\triangle HB'C' \sim \triangle OBC, BB', CC'</math> and <math>HO</math> are concurrent at point <math>P.</math>
  
−
In accordance with Claim, <math>\angle HUF = \angle AUF \implies</math> points <math>H</math> and <math>P</math> are isogonal conjugate with respect <math>\triangle UVW.</math>  
+
In accordance with <i><b>Claim,</b></i> <math>\angle HUF = \angle AUF \implies</math> points <math>H</math> and <math>P</math> are isogonal conjugate with respect <math>\triangle UVW.</math>  
  
−
<math>\angle HDE = \alpha - 90^\circ, \angle HCD = 90^\circ - \beta \implies</math>
+
<cmath>\angle HDE = \alpha - 90^\circ, \angle HCD = 90^\circ - \beta \implies</cmath>
  
−
<math>HB' = 2 HD \sin (\alpha - 90^\circ) = - 2 CD \tan(90^\circ- \beta) \cos \alpha = - 2 AC \cos \gamma \frac {\cos \beta}{\sin \beta} \cos \alpha = - 4 OB \cos A \cos B \cos C.</math>   
+
<cmath>HB' = 2 HD \sin (\alpha - 90^\circ) = - 2 CD \tan(90^\circ- \beta) \cos \alpha = - 2 AC \cos \gamma \frac {\cos \beta}{\sin \beta} \cos \alpha = - 4 OB \cos A \cos B \cos C.</cmath>   
−
<math>k = \frac {HB'}{OB} = \frac {HP}{OP}= - 4 \cos A \cos B \cos C \implies \frac {\vec {PH}}{\vec {OP}}= 4 \cos A \cos B \cos C.</math>
+
<cmath>k = \frac {HB'}{OB} = \frac {HP}{OP}= - 4 \cos A \cos B \cos C \implies \frac {\vec {PH}}{\vec {OP}}= 4 \cos A \cos B \cos C.</cmath>
  
 
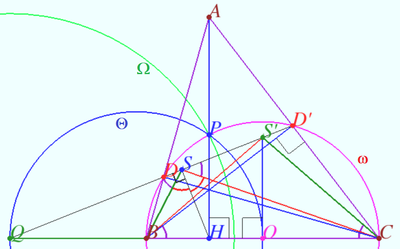
<i><b>Claim</b></i>
 
<i><b>Claim</b></i>
Line 48: Line 49:
 
Let <math>\Theta</math> be the circle with diameter <math>OQ.</math>
 
Let <math>\Theta</math> be the circle with diameter <math>OQ.</math>
  
−
We know that <math>OB = OP = OC = R, PH^2 = R^2 – OH^2 \implies</math>
+
Well known that <math>AH</math> is the polar of point <math>Q,</math> so <math>QO \cdot HO = QP^2 \implies QB \cdot QC = (QO – R) \cdot (QO + R) = QP^2</math>  <cmath>\implies P \in \Theta,  \Omega \perp \omega.</cmath>
−
<math>QP^2 + R^2 = (QH+ HO)^2 \implies P \in \Theta,  \Omega \perp \omega.</math>
+
 
 +
Let <math>I_{\Omega}</math> be inversion with respect <math>\Omega, I_{\Omega}(B) = C,  I_{\Omega}(H) = O,I_{\Omega}(D) = D'.</math>
 +
 
 +
Denote <math>I_{\Omega}(S) = S'.</math>
 +
 
 +
<cmath>HS \perp DD' \implies S'O \perp BC \implies BS' = CS' \implies \angle OCS' = \angle OBS'.</cmath>
 +
<cmath>\angle QSB = \angle QCS' = \angle OCS' = \angle OBS' = \angle CSS'.</cmath>
 +
<cmath>\angle BSH = 90 ^\circ  – \angle QSB = 90 ^\circ  – \angle CSS' =\angle CSH.</cmath>
 +
 
 +
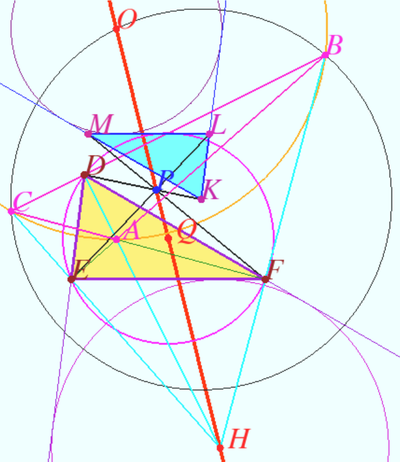
==Theorem 2==
 +
[[File:2016 USAMO 3e.png|400px|right]]
 +
Let <math>T_0 = \triangle ABC</math> be the base triangle, <math>T_1 = \triangle DEF</math> be orthic triangle of <math>T_0, T_2 = \triangle KLM</math> be Kosnita triangle of <math>T_0.</math> Then <math>\triangle T_1</math> and <math>\triangle T_2</math> are homothetic, the point <math>P,</math> center of this homothety lies on Euler line of <math>T_0,</math> the ratio of the homothety is <math>k =  \frac {\vec PH}{\vec OP} = 4 \cos A \cos B \cos C.</math>
 +
We recall that vertex of Kosnita triangle are:  <math>K</math> is the circumcenter of <math>\triangle OBC, L</math> is the circumcenter of <math>\triangle OAB, M</math> is the circumcenter of <math>\triangle OAC,</math> where <math>O</math> is circumcenter of <math>T_0.</math>
 +
 
 +
<i><b>Proof</b></i>
 +
 
 +
Let <math>H</math> be orthocenter of <math>T_0, Q</math> be the center of Nine-point circle of <math>T_0, HQO</math> is the Euler line of <math>T_0.</math>
 +
Well known that <math>EF</math> is antiparallel <math>BC</math> with respect <math>\angle A.</math>
  
−
Let <math>I_{\Omega}</math> be inversion with respect <math>\Omega, I_{\Omega}(B) = C.</math>
+
<math>LM</math> is the bisector of <math>AO,</math> therefore <math>LM</math> is antiparallel <math>BC</math> with respect <math>\angle A</math>
 +
<cmath>\implies LM||EF.</cmath>
 +
Similarly, <math>DE||KL, DF||KM \implies \triangle DEF</math> and <math>\triangle KLM</math> are homothetic.
  
−
Denote <math>I_{\Omega}(D) = D',  I_{\Omega}(S) = S',</math>  
+
Let <math>P</math> be the center of homothety.
−
<math>QH \cdot QO = QP^2 \implies I_{\Omega}(H) = O.</math>
 
−
<math>HS \perp DD' \implies S'O \perp BC \implies BS' = CS' \implies \angle OCS' = \angle OBS'.</math>
 
  
−
<math>\angle QSB = \angle QCS' = \angle OCS' = \angle OBS' = \angle CSS'.</math>
+
<math>H</math> is <math>D</math>-excenter of <math>\triangle DEF, O</math> is <math>K</math>-excenter of <math>\triangle KLM \implies</math>
 +
<math>P \in HO.</math>
  
−
<math>\angle BSH = 90 ^\circ  – \angle QSB = 90 ^\circ – \angle CSS' =\angle CSH.</math>
+
Denote <math>a = BC, \alpha = \angle A, \beta = \angle B, \gamma = \angle C, R</math> circumradius <math>\triangle ABC.</math>
 +
<math>\angle EHF = 180^\circ - \alpha, EF = BC |\cos \alpha| = 2R \sin \alpha |\cos \alpha|.</math>
 +
<cmath>LM = \frac {R}{2} (\tan \beta + \tan \gamma) = \frac {R \sin (\beta + \gamma)}{2 \cos \beta \cdot \cos \gamma} \implies</cmath>
 +
<cmath>k = \frac {DE}{KL} = 4\cos \alpha \cdot \cos \beta \cdot \cos \gamma \implies</cmath>
 +
<math>\frac {\vec {PH}}{\vec {OP}}= 4 \cos A \cos B \cos C \implies P</math> is the point  <math>X(24).</math>
  
−
<i><b>Theorem 2</b></i>
+
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
==Theorem 3==
 +
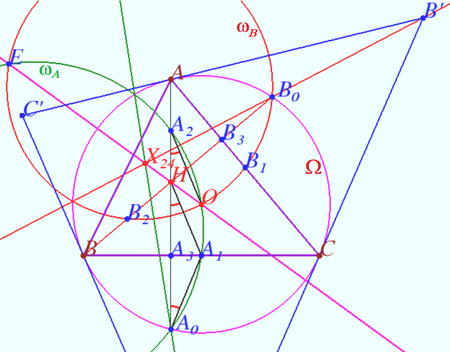
[[File:X24 as Exeter.png|450px|right]]
 +
Let <math>\triangle ABC</math> be the reference triangle (other than a right triangle). Let the altitudes through the vertices <math>A, B, C</math> meet the circumcircle <math>\Omega</math> of triangle <math>ABC</math> at <math>A_0, B_0,</math> and <math>C_0,</math> respectively. Let <math>A'B'C'</math> be the triangle formed by the tangents at <math>A, B,</math> and <math>C</math> to <math>\Omega.</math> (Let <math>A'</math> be the vertex opposite to the side formed by the tangent at the vertex A). Prove that the lines through <math>A_0A', B_0B',</math> and <math>C_0C'</math> are concurrent, the point of concurrence <math>X_{24}</math> lies on Euler line of triangle <math>ABC,  X_{24} = O + \frac {2}{J^2 + 1} (H – O), J = \frac {|OH|}{R}.</math>
  
−
Let <math>T_0 = \triangle ABC</math> be the base triangle, <math>T_1 = \triangle DEF</math> be orthic triangle of <math>T_0, T_2 = \triangle KLM</math> be Kosnita triangle. Then <math>\triangle T_1</math> and <math>\triangle T_2</math> are homothetic, the point <math>P,</math> center of this homothety lies on Euler line of <math>T_0,</math> the ratio of the homothety is <math>k =  \frac {\vec PH}{\vec OP} = 4 \cos A \cos B \cos C.</math>
+
<i><b>Proof</b></i>
−
We recall that vertex of Kosnita triangle are:  <math>K</math> is the circumcenter of <math>\triangle OBC, L</math> is the circumcenter of <math>\triangle OAB, M</math> is the circumcenter of <math>\triangle OAC,</math> where <math>O</math> is circumcenter of <math>T_0.</math>
+
 
 +
At first one can prove that lines <math>A_0A', B_0B',</math> and <math>C_0C'</math> are concurrent. This follows from the fact that lines <math>AA_0, BB_0,</math> and <math>CC_0</math> are concurrent at point <math>H</math> and <i><b>Mapping theorem</b></i> (see Exeter point <math>X_{22}).</math>
 +
 
 +
Let <math>A_1, B_1,</math> and <math>C_1</math> be the midpoints of <math>BC, AC,</math> and <math>AB,</math> respectively.
 +
 
 +
Let <math>A_2, B_2,</math> and <math>C_2</math> be the midpoints of <math>AH, BH,</math> and <math>CH,</math> respectively.
 +
 
 +
Let <math>A_3, B_3,</math> and <math>C_3</math> be the foots of altitudes from <math>A, B,</math> and <math>C,</math> respectively.
 +
 +
The points <math>A, A_2, H,</math> and <math>A_3</math> are collinear. Similarly the points <math>B, B_2, H, B_3</math> and <math>C, C_2, H, C_3</math> are collinear.
 +
 
 +
Denote <math>I_{\Omega}</math> the inversion with respect <math>\Omega.</math>  It is evident that <math>I_{\Omega}(A') = A_1, I_{\Omega}(B') = B_1, I_{\Omega}(C') = C_1, I_{\Omega}(A_0) = A_0, I_{\Omega}(B_0) = B_0, I_{\Omega}(C_0) = C_0.</math>
 +
 
 +
Denote <math>\omega_A = I_{\Omega}(A'A_0), \omega_B =  I_{\Omega}(B'B_0)  \omega_C =  I_{\Omega}(C'C_0) \implies</math>
 +
<cmath>A_0 \in \omega_A, A_1 \in \omega_A, O \in \omega_A, B_0 \in \omega_B, B_1 \in \omega_B, O \in \omega_B \implies\ O = \omega_A \cap \omega_B \cap \omega_C.</cmath>
 +
 
 +
It is known that <math>A_2O = HA_1 = A_0A_1, A_2O || HA_1 \implies \angle OA_2A_0 = \angle A_1A_0A_2, OA_1 ||A_0A_2 \implies A_2 \in \omega_A.</math>
 +
 
 +
Similarly, <math>B_2 \in \omega_B, C_2 \in \omega_C.</math>
 +
 
 +
We use <i><b>Claim</b></i> and get that the power of point <math>H</math> with respect each circle <math>\omega_X</math> is  
 +
<cmath>HA_2 \cdot HA_0 =  HB_2 \cdot HB_0 = HC_2 \cdot HC_0 = \frac {R^2 \cdot (1-J^2)} {2}.</cmath>
 
   
 
   
 +
<math>H = AA_0 \cap BB_0 \cap CC_0 \implies H</math> lies on common radical axis of <math>\omega_A, \omega_B,</math> and <math>\omega_C.</math>
 +
 +
Therefore second crosspoint of these circles point <math>E</math> lies on line <math>OH</math> which is the Euler line of <math>\triangle ABC \implies</math> <math>X_{24} = I_{\Omega}(E)</math> lies on the same Euler line as desired.
 +
 +
Last we will find the length of <math>OX_{24}.</math>
 +
<cmath>OH \cdot HE = \frac {R^2 \cdot (1–J^2)} {2}.</cmath>
 +
<cmath>OE \cdot OX_{24} = (OH + HE)\cdot OX_{24} = R^2.</cmath>
 +
<math>\frac {OX_{24}}{OH} =  \frac {R^2}{OH^2 + OH \cdot HE} = \frac {1}{J^2 + \frac {1– J^2} {2}} =
 +
\frac {2}{1+J^2},</math> as desired.
 +
 +
<i><b>Claim</b></i>
 +
[[File:AH HF.png|400px|right]]
 +
Let <math>AD, BE,</math> and <math>CF</math> be the heights of <math>\triangle ABC, H = AD \cap BE \cap CF.</math>
 +
 +
Prove that <math>AH \cdot HD = \frac {R^2 (1 – J^2)}{2},</math>
 +
 +
where <math>R</math> and <math>O</math> are circumradius and circumcenter of <math>\triangle ABC, J = \frac {OH}{R}.</math>
 +
 +
<i><b>Proof</b></i>
 +
 +
It is known that <math>\triangle ABC \sim \triangle AEF.</math>
 +
<math>k = \frac {AF} {AC} = \cos A \implies AH = 2 R k = 2 R \cos A.</math>
 +
 +
Similarly <math>BH =  2 R \cos B, DH = BH \sin \angle CBE = BH \cos C = 2R \cos B \cos C.</math>
 +
 +
Therefore <math>AH \cdot HD = 4R^2 \cos A \cos B \cos C.</math>
 +
 +
<cmath>J^2 = \frac {HO^2}{R^2} = 1 – 8 \cos A \cos B \cos C \ \implies AH \cdot HD = \frac {R^2 (1 – J^2)}{2}.</cmath>
 +
 
'''vladimir.shelomovskii@gmail.com, vvsss'''
 
'''vladimir.shelomovskii@gmail.com, vvsss'''

Latest revision as of 14:34, 25 November 2022

Kimberling's point X(24)

2016 USAMO 3g.png

Kimberling defined point X(24) as perspector of $\triangle ABC$ and Orthic Triangle of the Orthic Triangle of $\triangle ABC$.

Theorem 1

Denote $T_0$ obtuse or acute $\triangle ABC.$ Let $T_0$ be the base triangle, $T_1 = \triangle DEF$ be Orthic triangle of $T_0, T_2 = \triangle UVW$ be Orthic Triangle of $T_1$. Let $O$ and $H$ be the circumcenter and orthocenter of $T_0.$

Then $\triangle T_0$ and $\triangle T_2$ are homothetic, the point $P,$ center of this homothety lies on Euler line $OH$ of $T_0.$

The ratio of the homothety is $k = \frac {\vec {PH}}{\vec {OP}}= 4 \cos A \cos B \cos C.$

Proof

WLOG, we use case $\angle A = \alpha > 90^\circ.$

Let $B'$ be reflection $H$ in $DE.$ In accordance with Claim, $\angle BVD = \angle HVE \implies B', V,$ and $B$ are collinear.

Similarly, $C, W,$ and $C',$ were $C'$ is reflection $H$ in $DF,$ are collinear.

Denote $\angle ABC = \beta = \angle CHD, \angle ACB = \gamma = \angle BHD \implies$

$\angle HDF = \angle HDE = \angle DHB' = \angle DHC' = 180^\circ - \alpha.$

$B'C' \perp HD, BC \perp HD \implies BC|| B'C'.$ $OB = OC, HB' = HC', \angle BOC = \angle B'HC' = 360^\circ - 2 \alpha \implies OB ||HB', OC || HC' \implies$

$\triangle HB'C' \sim \triangle OBC, BB', CC'$ and $HO$ are concurrent at point $P.$

In accordance with Claim, $\angle HUF = \angle AUF \implies$ points $H$ and $P$ are isogonal conjugate with respect $\triangle UVW.$

\[\angle HDE = \alpha - 90^\circ, \angle HCD = 90^\circ - \beta \implies\]

\[HB' = 2 HD \sin (\alpha - 90^\circ) = - 2 CD \tan(90^\circ- \beta) \cos \alpha = - 2 AC \cos \gamma \frac {\cos \beta}{\sin \beta} \cos \alpha = - 4 OB \cos A \cos B \cos C.\] \[k = \frac {HB'}{OB} = \frac {HP}{OP}= - 4 \cos A \cos B \cos C \implies \frac {\vec {PH}}{\vec {OP}}= 4 \cos A \cos B \cos C.\]

Claim

2016 3 Lemma.png

Let $\triangle ABC$ be an acute triangle, and let $AH, BD',$ and $CD$ denote its altitudes. Lines $DD'$ and $BC$ meet at $Q, HS \perp DD'.$ Prove that $\angle BSH = \angle CSH.$

Proof

Let $\omega$ be the circle $BCD'D$ centered at $O (O$ is midpoint $BC).$

Let $\omega$ meet $AH$ at $P.$ Let $\Omega$ be the circle centered at $Q$ with radius $QP.$

Let $\Theta$ be the circle with diameter $OQ.$

Well known that $AH$ is the polar of point $Q,$ so $QO \cdot HO = QP^2 \implies QB \cdot QC = (QO – R) \cdot (QO + R) = QP^2$ \[\implies P \in \Theta, \Omega \perp \omega.\]

Let $I_{\Omega}$ be inversion with respect $\Omega, I_{\Omega}(B) = C, I_{\Omega}(H) = O,I_{\Omega}(D) = D'.$

Denote $I_{\Omega}(S) = S'.$

\[HS \perp DD' \implies S'O \perp BC \implies BS' = CS' \implies \angle OCS' = \angle OBS'.\] \[\angle QSB = \angle QCS' = \angle OCS' = \angle OBS' = \angle CSS'.\] \[\angle BSH = 90 ^\circ – \angle QSB = 90 ^\circ – \angle CSS' =\angle CSH.\]

Theorem 2

2016 USAMO 3e.png

Let $T_0 = \triangle ABC$ be the base triangle, $T_1 = \triangle DEF$ be orthic triangle of $T_0, T_2 = \triangle KLM$ be Kosnita triangle of $T_0.$ Then $\triangle T_1$ and $\triangle T_2$ are homothetic, the point $P,$ center of this homothety lies on Euler line of $T_0,$ the ratio of the homothety is $k = \frac {\vec PH}{\vec OP} = 4 \cos A \cos B \cos C.$ We recall that vertex of Kosnita triangle are: $K$ is the circumcenter of $\triangle OBC, L$ is the circumcenter of $\triangle OAB, M$ is the circumcenter of $\triangle OAC,$ where $O$ is circumcenter of $T_0.$

Proof

Let $H$ be orthocenter of $T_0, Q$ be the center of Nine-point circle of $T_0, HQO$ is the Euler line of $T_0.$ Well known that $EF$ is antiparallel $BC$ with respect $\angle A.$

$LM$ is the bisector of $AO,$ therefore $LM$ is antiparallel $BC$ with respect $\angle A$ \[\implies LM||EF.\] Similarly, $DE||KL, DF||KM \implies \triangle DEF$ and $\triangle KLM$ are homothetic.

Let $P$ be the center of homothety.

$H$ is $D$-excenter of $\triangle DEF, O$ is $K$-excenter of $\triangle KLM \implies$ $P \in HO.$

Denote $a = BC, \alpha = \angle A, \beta = \angle B, \gamma = \angle C, R$ circumradius $\triangle ABC.$ $\angle EHF = 180^\circ - \alpha, EF = BC |\cos \alpha| = 2R \sin \alpha |\cos \alpha|.$ \[LM = \frac {R}{2} (\tan \beta + \tan \gamma) = \frac {R \sin (\beta + \gamma)}{2 \cos \beta \cdot \cos \gamma} \implies\] \[k = \frac {DE}{KL} = 4\cos \alpha \cdot \cos \beta \cdot \cos \gamma \implies\] $\frac {\vec {PH}}{\vec {OP}}= 4 \cos A \cos B \cos C \implies P$ is the point $X(24).$

vladimir.shelomovskii@gmail.com, vvsss

Theorem 3

X24 as Exeter.png

Let $\triangle ABC$ be the reference triangle (other than a right triangle). Let the altitudes through the vertices $A, B, C$ meet the circumcircle $\Omega$ of triangle $ABC$ at $A_0, B_0,$ and $C_0,$ respectively. Let $A'B'C'$ be the triangle formed by the tangents at $A, B,$ and $C$ to $\Omega.$ (Let $A'$ be the vertex opposite to the side formed by the tangent at the vertex A). Prove that the lines through $A_0A', B_0B',$ and $C_0C'$ are concurrent, the point of concurrence $X_{24}$ lies on Euler line of triangle $ABC, X_{24} = O + \frac {2}{J^2 + 1} (H – O), J = \frac {|OH|}{R}.$

Proof

At first one can prove that lines $A_0A', B_0B',$ and $C_0C'$ are concurrent. This follows from the fact that lines $AA_0, BB_0,$ and $CC_0$ are concurrent at point $H$ and Mapping theorem (see Exeter point $X_{22}).$

Let $A_1, B_1,$ and $C_1$ be the midpoints of $BC, AC,$ and $AB,$ respectively.

Let $A_2, B_2,$ and $C_2$ be the midpoints of $AH, BH,$ and $CH,$ respectively.

Let $A_3, B_3,$ and $C_3$ be the foots of altitudes from $A, B,$ and $C,$ respectively.

The points $A, A_2, H,$ and $A_3$ are collinear. Similarly the points $B, B_2, H, B_3$ and $C, C_2, H, C_3$ are collinear.

Denote $I_{\Omega}$ the inversion with respect $\Omega.$ It is evident that $I_{\Omega}(A') = A_1, I_{\Omega}(B') = B_1, I_{\Omega}(C') = C_1, I_{\Omega}(A_0) = A_0, I_{\Omega}(B_0) = B_0, I_{\Omega}(C_0) = C_0.$

Denote $\omega_A = I_{\Omega}(A'A_0), \omega_B = I_{\Omega}(B'B_0) \omega_C = I_{\Omega}(C'C_0) \implies$ \[A_0 \in \omega_A, A_1 \in \omega_A, O \in \omega_A, B_0 \in \omega_B, B_1 \in \omega_B, O \in \omega_B \implies\ O = \omega_A \cap \omega_B \cap \omega_C.\]

It is known that $A_2O = HA_1 = A_0A_1, A_2O || HA_1 \implies \angle OA_2A_0 = \angle A_1A_0A_2, OA_1 ||A_0A_2 \implies A_2 \in \omega_A.$

Similarly, $B_2 \in \omega_B, C_2 \in \omega_C.$

We use Claim and get that the power of point $H$ with respect each circle $\omega_X$ is \[HA_2 \cdot HA_0 = HB_2 \cdot HB_0 = HC_2 \cdot HC_0 = \frac {R^2 \cdot (1-J^2)} {2}.\]

$H = AA_0 \cap BB_0 \cap CC_0 \implies H$ lies on common radical axis of $\omega_A, \omega_B,$ and $\omega_C.$

Therefore second crosspoint of these circles point $E$ lies on line $OH$ which is the Euler line of $\triangle ABC \implies$ $X_{24} = I_{\Omega}(E)$ lies on the same Euler line as desired.

Last we will find the length of $OX_{24}.$ \[OH \cdot HE = \frac {R^2 \cdot (1–J^2)} {2}.\] \[OE \cdot OX_{24} = (OH + HE)\cdot OX_{24} = R^2.\] $\frac {OX_{24}}{OH} = \frac {R^2}{OH^2 + OH \cdot HE} = \frac {1}{J^2 + \frac {1– J^2} {2}} = \frac {2}{1+J^2},$ as desired.

Claim

AH HF.png

Let $AD, BE,$ and $CF$ be the heights of $\triangle ABC, H = AD \cap BE \cap CF.$

Prove that $AH \cdot HD = \frac {R^2 (1 – J^2)}{2},$

where $R$ and $O$ are circumradius and circumcenter of $\triangle ABC, J = \frac {OH}{R}.$

Proof

It is known that $\triangle ABC \sim \triangle AEF.$ $k = \frac {AF} {AC} = \cos A \implies AH = 2 R k = 2 R \cos A.$

Similarly $BH = 2 R \cos B, DH = BH \sin \angle CBE = BH \cos C = 2R \cos B \cos C.$

Therefore $AH \cdot HD = 4R^2 \cos A \cos B \cos C.$

\[J^2 = \frac {HO^2}{R^2} = 1 – 8 \cos A \cos B \cos C \ \implies AH \cdot HD = \frac {R^2 (1 – J^2)}{2}.\]

vladimir.shelomovskii@gmail.com, vvsss

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Kimberling’s_point_X(24)&oldid=182996"