Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2007 AMC 10B Problems/Problem 21"

m (→‎Solution 2)
m (→‎Solution 2)
Line 34: Line 34:
 
<cmath>\frac{ZB}{l} = \frac{4}{5} \rightarrow ZB = \frac{4}{5}l</cmath>
 
<cmath>\frac{ZB}{l} = \frac{4}{5} \rightarrow ZB = \frac{4}{5}l</cmath>
  
−
But then <math>\frac{5}{3}l+\frac{4}{5}l = CZ+ZB = CB = 4 \longrightarrow \frac{37}{15}l=4 \longrightarrow l = \frac{60}{37} \Longrightarrow \mathrm{(B)}</math>
+
But then <math>\frac{5}{3}l+\frac{4}{5}l = CZ+ZB = CB = 4 \longrightarrow \frac{37}{15}l=4 \longrightarrow l = \frac{60}{37} \Longrightarrow \boxed{\mathrm{(B)}\frac{60}{37}}</math>
  
 
==See Also==
 
==See Also==

Revision as of 19:02, 21 December 2018

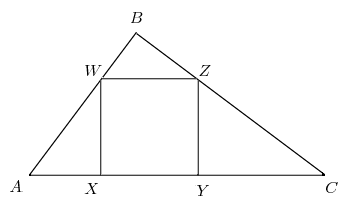
Problem

Right $\triangle ABC$ has $AB=3, BC=4,$ and $AC=5.$ Square $XYZW$ is inscribed in $\triangle ABC$ with $X$ and $Y$ on $\overline{AC}, W$ on $\overline{AB},$ and $Z$ on $\overline{BC}.$ What is the side length of the square?

$\textbf{(A) } \frac{3}{2} \qquad\textbf{(B) } \frac{60}{37} \qquad\textbf{(C) } \frac{12}{7} \qquad\textbf{(D) } \frac{23}{13} \qquad\textbf{(E)} 2$

Solution 1

2007AMC10B21.png

There are many similar triangles in the diagram, but we will only use $\triangle WBZ \sim \triangle ABC.$ If $h$ is the altitude from $B$ to $AC$ and $s$ is the sidelength of the square, then $h-s$ is the altitude from $B$ to $WZ.$ By similar triangles, \begin{align*} \frac{h-s}{s}&=\frac{h}{5}\\ 5h-5s&=hs\\ 5h&=s(h+5)\\ s&=\frac{5h}{h+5} \end{align*}

Find the length of the altitude of $\triangle ABC.$ Since it is a right triangle, the area of $\triangle ABC$ is $\frac{1}{2}(3)(4) = 6.$

The area can also be expressed as $\frac{1}{2}(5)(h),$ so $\frac{5}{2}h=6 \longrightarrow h=2.4.$

Substitute back into $s.$

\[s=\frac{5h}{h+5} = \frac{12}{7.4} = \boxed{\mathrm{(B) \ } \frac{60}{37}}\]

Solution 2

Let $l$ be the side length of the inscribed square. Note that $\triangle ZYC \sim \triangle WBZ \sim \triangle ABC$.

Then we can setup the following ratios:

\[\frac{CZ}{l} = \frac{5}{3} \rightarrow CZ = \frac{5}{3}l\] \[\frac{ZB}{l} = \frac{4}{5} \rightarrow ZB = \frac{4}{5}l\]

But then $\frac{5}{3}l+\frac{4}{5}l = CZ+ZB = CB = 4 \longrightarrow \frac{37}{15}l=4 \longrightarrow l = \frac{60}{37} \Longrightarrow \boxed{\mathrm{(B)}\frac{60}{37}}$

See Also

2007 AMC 10B (Problems • Answer Key • Resources)
Preceded by
Problem 20 		Followed by
Problem 22
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2007_AMC_10B_Problems/Problem_21&oldid=99652"