Difference between revisions of "1977 Canadian MO Problems/Problem 2"
(box) |
|||
| Line 1: | Line 1: | ||
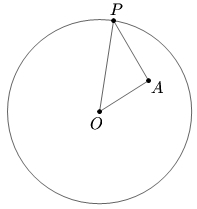
| − | Let <math> | + | Let <math>O</math> be the center of a circle and <math>A</math> be a fixed interior point of the circle different from <math>O.</math> Determine all points <math>P</math> on the circumference of the circle such that the angle <math>OPA</math> is a maximum. |
[[Image:CanadianMO-1977-2.jpg]] | [[Image:CanadianMO-1977-2.jpg]] | ||
== Solution == | == Solution == | ||
| + | {{solution}} | ||
| − | + | {{Old CanadaMO box|num-b=1|num-a=3|year=1977}} | |
| − | == | ||
| − | |||
| − | |||
[[Category:Olympiad Geometry Problems]] | [[Category:Olympiad Geometry Problems]] | ||
Revision as of 21:49, 17 November 2007
Let 
be the center of a circle and 
be a fixed interior point of the circle different from 
Determine all points 
on the circumference of the circle such that the angle 
is a maximum.
Solution
This problem needs a solution. If you have a solution for it, please help us out by adding it.
| 1977 Canadian MO (Problems) | ||
| Preceded by Problem 1 |
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • | Followed by Problem 3 |
