Complete Quadrilateral
Complete quadrilateral
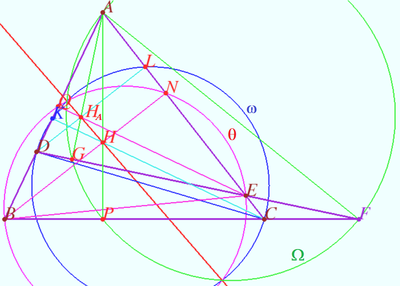
Let four lines made four triangles of a complete quadrilateral. In the diagram these are ![]() One can see some of the properties of this configuration and their proof using the following links.
One can see some of the properties of this configuration and their proof using the following links.
Radical axis
Let four lines made four triangles of a complete quadrilateral. In the diagram these are ![]()
Let points ![]() and
and ![]() be the orthocenters of
be the orthocenters of ![]() and
and ![]() respectively.
respectively.
Let circles ![]() and
and ![]() be the circles with diameters
be the circles with diameters ![]() and
and ![]() respectively.
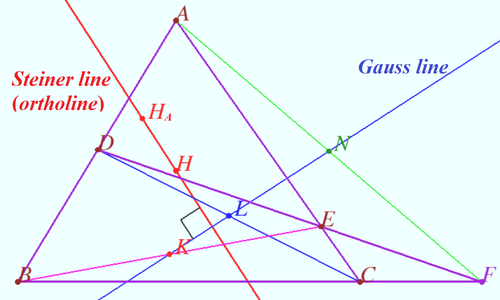
Prove that Steiner line
respectively.
Prove that Steiner line ![]() is the radical axis of
is the radical axis of ![]() and
and ![]()
Proof
Let points ![]() and
and ![]() be the foots of perpendiculars
be the foots of perpendiculars ![]() and
and ![]() respectively.
respectively.
Denote ![]() power of point
power of point ![]() with respect the circle
with respect the circle ![]()
![]()
![]()
![]()
![]()
![]()
![]() Therefore power of point
Therefore power of point ![]() with respect these three circles is the same. These points lies on the common radical axis of
with respect these three circles is the same. These points lies on the common radical axis of ![]() and
and ![]() Steiner line
Steiner line ![]() is the radical axis as desired.
is the radical axis as desired.
vladimir.shelomovskii@gmail.com, vvsss
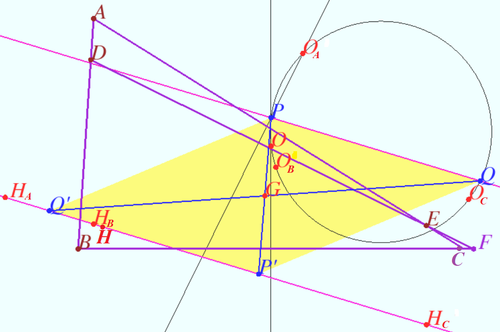
Newton–Gauss line
Let four lines made four triangles of a complete quadrilateral.
In the diagram these are ![]()
Let points ![]() and
and ![]() be the midpoints of
be the midpoints of ![]() and
and ![]() respectively.
respectively.
Let points ![]() and
and ![]() be the orthocenters of
be the orthocenters of ![]() and
and ![]() respectively.
respectively.
Prove that Steiner line ![]() is perpendicular to Gauss line
is perpendicular to Gauss line ![]()
Proof
Points ![]() and
and ![]() are the centers of circles with diameters
are the centers of circles with diameters ![]() and
and ![]() respectively.
respectively.
Steiner line ![]() is the radical axis of these circles.
is the radical axis of these circles.
Therefore ![]() as desired.
as desired.
vladimir.shelomovskii@gmail.com, vvsss
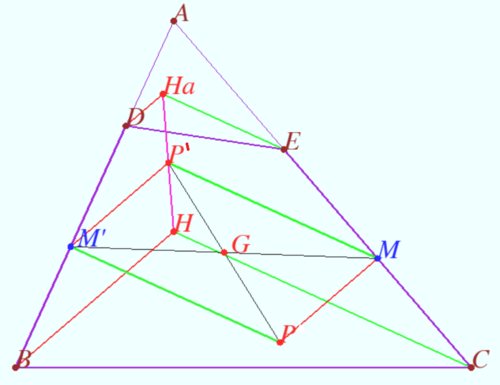
Shatunov-Tokarev line
Let the complete quadrilateral ABCDEF be labeled as in the diagram. Quadrilateral ![]() is not cyclic.
is not cyclic.
Let points ![]() be the orthocenters and points
be the orthocenters and points ![]() be the circumcenters of
be the circumcenters of ![]() and
and ![]() respectively.
respectively.
Let bisector ![]() cross bisector
cross bisector ![]() at point
at point ![]() Let bisector
Let bisector ![]() cross bisector
cross bisector ![]() at point
at point ![]()
Prove that
a) points ![]() and
and ![]() lie on circumcircle of
lie on circumcircle of ![]()
b) line ![]() is symmetric to Steiner line with respect centroid of
is symmetric to Steiner line with respect centroid of ![]()
I suppose that this line was found independently by two young mathematicians Leonid Shatunov and Alexander Tokarev in 2022. I would be grateful for information on whether this line was previously known.
Proof
a) Points ![]() and
and ![]() lies on bisector of
lies on bisector of ![]() points
points ![]() and
and ![]() lies on bisector of
lies on bisector of ![]()
![]() circle
circle ![]()
Similarly ![]() circle
circle ![]() as desired.
as desired.
b) Let ![]() and
and ![]() be midpoints of
be midpoints of ![]() and
and ![]() respectively.
respectively.
It is clear that ![]() is centroid of
is centroid of ![]()
![]() (midline of trapezium
(midline of trapezium ![]()
![]()
![]() (midline of trapezium
(midline of trapezium ![]()
![]() is parallelogram.
is parallelogram.
Similarly one can prove that point ![]() the midpoint of
the midpoint of ![]() is symmetric to
is symmetric to ![]() with respect
with respect ![]()
Therefore line ![]() coincide with Steiner line and line
coincide with Steiner line and line ![]() is symmetric to Steiner line with respect
is symmetric to Steiner line with respect ![]() and is parallel to this line.
and is parallel to this line.
vladimir.shelomovskii@gmail.com, vvsss