Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Trigonometric identities"

(→‎Pythagorean Identities: lists not tables 2)
(lists not tables 3)
Line 38: Line 38:
 
Once we have formulas for angle addition, angle subtraction is rather easy to derive.  For example, we just look at <math> \sin(\alpha+(-\beta))</math> and we can derive the sine angle subtraction formula using the sine angle addition formula.
 
Once we have formulas for angle addition, angle subtraction is rather easy to derive.  For example, we just look at <math> \sin(\alpha+(-\beta))</math> and we can derive the sine angle subtraction formula using the sine angle addition formula.
  
−
{| style="width:100%; height:130px; margin: 1em auto 1em auto"
+
*<math> \sin(\alpha + \beta) = \sin \alpha\cos \beta +\sin \beta \cos \alpha</math> || <math>\sin(\alpha - \beta) = \sin \alpha \cos \beta - \sin \beta \cos \alpha</math>
−
|-
+
*<math> \cos(\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta </math> || <math>\cos(\alpha - \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta</math>
−
| <math> \sin(\alpha + \beta) = \sin \alpha\cos \beta +\sin \beta \cos \alpha</math> || <math>\sin(\alpha - \beta) = \sin \alpha \cos \beta - \sin \beta \cos \alpha</math>
+
*<math>\tan(\alpha + \beta) = \frac{\tan \alpha + \tan \beta}{1-\tan \alpha \tan \beta} </math> || <math>\tan(\alpha - \beta) = \frac{\tan \alpha - \tan \beta}{1+\tan \alpha \tan \beta} </math>
−
|-
+
 
−
| <math> \cos(\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta </math> || <math>\cos(\alpha - \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta</math>
 
−
|-
 
−
| <math>\tan(\alpha + \beta) = \frac{\tan \alpha + \tan \beta}{1-\tan \alpha \tan \beta} </math> || <math>\tan(\alpha - \beta) = \frac{\tan \alpha - \tan \beta}{1+\tan \alpha \tan \beta} </math>
 
−
|}
 
 
We can prove <math> \cos(\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta </math> easily by using <math> \sin(\alpha + \beta) = \sin \alpha\cos \beta +\sin \beta \cos \alpha</math> and <math>\sin(x)=\cos(90-x)</math>.
 
We can prove <math> \cos(\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta </math> easily by using <math> \sin(\alpha + \beta) = \sin \alpha\cos \beta +\sin \beta \cos \alpha</math> and <math>\sin(x)=\cos(90-x)</math>.
  
Line 58: Line 54:
 
Double angle identities are easily derived from the angle addition formulas by just letting <math> \alpha = \beta </math>.  Doing so yields:
 
Double angle identities are easily derived from the angle addition formulas by just letting <math> \alpha = \beta </math>.  Doing so yields:
  
−
{| style="height:200px; margin: 1em auto 1em auto"
+
<math>\sin 2\alpha = </math>2\sin \alpha \cos \alpha<math>
−
|-
+
</math>\cos 2\alpha = \cos^2 \alpha - \sin^2 \alpha<math>
−
| <math>\sin 2\alpha </math> || = || <math>2\sin \alpha \cos \alpha</math>
+
</math>=2\cos^2 \alpha - 1<math>
−
|-
+
</math>=1-2\sin^2 \alpha<math>
−
| <math>\cos 2\alpha </math> || = || <math>\cos^2 \alpha - \sin^2 \alpha</math>
+
</math>\tan 2\alpha <math> || = || </math>\frac{2\tan \alpha}{1-\tan^2\alpha} <math>
−
|-
+
 
−
| || = || <math>2\cos^2 \alpha - 1</math>
 
−
|-
 
−
| || = || <math>1-2\sin^2 \alpha</math>
 
−
|-
 
−
| <math>\tan 2\alpha </math> || = || <math>\frac{2\tan \alpha}{1-\tan^2\alpha} </math>
 
−
|}
 
  
  
  
 
== Half Angle Identities ==
 
== Half Angle Identities ==
−
Using the double angle identities, we can now derive half angle identities.  The double angle formula for cosine tells us <math>\cos 2\alpha = 2\cos^2 \alpha - 1 </math>.  Solving for <math>\cos \alpha </math> we get <math>\cos \alpha =\pm \sqrt{\frac{1 + \cos 2\alpha}2}</math> where we look at the quadrant of <math>\alpha </math> to decide if it's positive or negative.  Likewise, we can use the fact that <math>\cos 2\alpha = 1 - 2\sin^2 \alpha </math> to find a half angle identity for sine.  Then, to find a half angle identity for tangent, we just use the fact that <math>\tan \frac x2 =\frac{\sin \frac x2}{\cos \frac x2} </math> and plug in the half angle identities for sine and cosine.
+
Using the double angle identities, we can now derive half angle identities.  The double angle formula for cosine tells us </math>\cos 2\alpha = 2\cos^2 \alpha - 1 <math>.  Solving for </math>\cos \alpha <math> we get </math>\cos \alpha =\pm \sqrt{\frac{1 + \cos 2\alpha}2}<math> where we look at the quadrant of </math>\alpha <math> to decide if it's positive or negative.  Likewise, we can use the fact that </math>\cos 2\alpha = 1 - 2\sin^2 \alpha <math> to find a half angle identity for sine.  Then, to find a half angle identity for tangent, we just use the fact that </math>\tan \frac x2 =\frac{\sin \frac x2}{\cos \frac x2} <math> and plug in the half angle identities for sine and cosine.
  
 
To summarize:
 
To summarize:
  
−
{| style="height:150px; margin: 1em auto 1em auto"
+
</math> \sin \frac{\theta}2 = \pm \sqrt{\frac{1-\cos \theta}2} <math>
−
|-
+
</math> \cos \frac{\theta}2 = \pm \sqrt{\frac{1+\cos \theta}2} <math>
−
| <math> \sin \frac{\theta}2 = \pm \sqrt{\frac{1-\cos \theta}2} </math>
+
</math> \tan \frac{\theta}2 = \pm \sqrt{\frac{1-\cos \theta}{1+\cos \theta}} <math>
−
|-
+
 
−
| <math> \cos \frac{\theta}2 = \pm \sqrt{\frac{1+\cos \theta}2} </math>
 
−
|-
 
−
| <math> \tan \frac{\theta}2 = \pm \sqrt{\frac{1-\cos \theta}{1+\cos \theta}} </math>
 
−
|}
 
  
  
  
 
== Even-Odd Identities ==
 
== Even-Odd Identities ==
−
<math>\sin (-\theta) = -\sin (\theta) </math>
+
</math>\sin (-\theta) = -\sin (\theta) <math>
  
−
<math>\cos (-\theta) = \cos (\theta) </math>
+
</math>\cos (-\theta) = \cos (\theta) <math>
  
−
<math>\tan (-\theta) = -\tan (\theta) </math>
+
</math>\tan (-\theta) = -\tan (\theta) <math>
  
−
<math>\csc (-\theta) = -\csc (\theta) </math>
+
</math>\csc (-\theta) = -\csc (\theta) <math>
  
−
<math>\sec (-\theta) = \sec (\theta) </math>
+
</math>\sec (-\theta) = \sec (\theta) <math>
  
−
<math>\cot (-\theta) = -\cot (\theta) </math>
+
</math>\cot (-\theta) = -\cot (\theta) <math>
  
  
Line 107: Line 93:
 
(Otherwise known as sum-to-product identities)
 
(Otherwise known as sum-to-product identities)
  
−
* <math>\sin \theta \pm \sin \gamma = 2 \sin \frac{\theta\pm \gamma}2 \cos \frac{\theta\mp \gamma}2</math>
+
* </math>\sin \theta \pm \sin \gamma = 2 \sin \frac{\theta\pm \gamma}2 \cos \frac{\theta\mp \gamma}2<math>
−
* <math>\cos \theta + \cos \gamma = 2 \cos \frac{\theta+\gamma}2 \cos \frac{\theta-\gamma}2</math>
+
* </math>\cos \theta + \cos \gamma = 2 \cos \frac{\theta+\gamma}2 \cos \frac{\theta-\gamma}2<math>
−
* <math>\cos \theta - \cos \gamma = -2 \sin \frac{\theta+\gamma}2 \sin \frac{\theta-\gamma}2</math>
+
* </math>\cos \theta - \cos \gamma = -2 \sin \frac{\theta+\gamma}2 \sin \frac{\theta-\gamma}2<math>
  
  
Line 117: Line 103:
 
The extended [[Law of Sines]] states
 
The extended [[Law of Sines]] states
  
−
*<math>\frac a{\sin A} = \frac b{\sin B} = \frac c{\sin C} = 2R.</math>
+
*</math>\frac a{\sin A} = \frac b{\sin B} = \frac c{\sin C} = 2R.<math>
  
 
== Law of Cosines ==
 
== Law of Cosines ==
Line 123: Line 109:
 
The [[Law of Cosines]] states  
 
The [[Law of Cosines]] states  
  
−
*<math>a^2 = b^2 + c^2 - 2bc\cos A. </math>
+
*</math>a^2 = b^2 + c^2 - 2bc\cos A. <math>
  
 
== Law of Tangents ==
 
== Law of Tangents ==
Line 129: Line 115:
 
The [[Law of Tangents]] states
 
The [[Law of Tangents]] states
  
−
*<math>\frac{b - c}{b + c} = \frac{\tan\frac 12(B-C)}{\tan \frac 12(B+C)}.</math>
+
*</math>\frac{b - c}{b + c} = \frac{\tan\frac 12(B-C)}{\tan \frac 12(B+C)}.<math>
  
 
== Other Identities =
 
== Other Identities =
−
*<math>|1-e^{i\theta}|=2\sin\frac{\theta}{2}</math>
+
*</math>|1-e^{i\theta}|=2\sin\frac{\theta}{2}$
  
 
==See also==
 
==See also==

Revision as of 18:16, 25 October 2007

Trigonometric identities are used to manipulate trig equations in certain ways. Here is a list of them:

Basic Definitions

The six basic trigonometric functions can be defined using a right triangle:

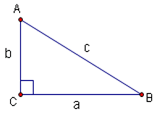
Righttriangle.png


The six trig functions are sine, cosine, tangent, cosecant, secant, and cotangent. They are abbreviated by using the first three letters of their name (except for cosecant which uses $\csc$). They are defined as follows:

  • $\sin A = \frac ac$
  • $\csc A = \frac ca$
  • $\cos A = \frac bc$
  • $\sec A = \frac cb$
  • $\tan A = \frac ab$
  • $\cot A = \frac ba$

Reciprocal Relations

From the last section, it is easy to see that the following hold:

  • $\sin A = \frac 1{\csc A}$
  • $\cos A = \frac 1{\sec A}$
  • $\tan A = \frac 1{\cot A}$


Another useful identity that isn't a reciprocal relation is that $\tan A =\frac{\sin A}{\cos A}$.

Pythagorean Identities

Using the Pythagorean Theorem on our triangle above, we know that $a^2 + b^2 = c^2$. If we divide by $c^2$ we get $\left(\frac ac\right)^2 + \left(\frac bc\right)^2 = 1$ which is just $\sin^2 A + \cos^2 A =1$. Dividing by $a^2$ or $b^2$ instead produces two other similar identities. The Pythagorean Identities are listed below:

  • $\sin^2x + \cos^2x = 1$
  • $1 + \cot^2x = \csc^2x$
  • $\tan^2x + 1 = \sec^2x$

(Note that the second two are easily derived by dividing the first by $\cos^2x$ and $\sin^2x$)

Angle Addition/Subtraction Identities

Once we have formulas for angle addition, angle subtraction is rather easy to derive. For example, we just look at $\sin(\alpha+(-\beta))$ and we can derive the sine angle subtraction formula using the sine angle addition formula.

  • $\sin(\alpha + \beta) = \sin \alpha\cos \beta +\sin \beta \cos \alpha$ || $\sin(\alpha - \beta) = \sin \alpha \cos \beta - \sin \beta \cos \alpha$
  • $\cos(\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta$ || $\cos(\alpha - \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta$
  • $\tan(\alpha + \beta) = \frac{\tan \alpha + \tan \beta}{1-\tan \alpha \tan \beta}$ || $\tan(\alpha - \beta) = \frac{\tan \alpha - \tan \beta}{1+\tan \alpha \tan \beta}$

We can prove $\cos(\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta$ easily by using $\sin(\alpha + \beta) = \sin \alpha\cos \beta +\sin \beta \cos \alpha$ and $\sin(x)=\cos(90-x)$.


$\cos (\alpha + \beta)$

$= \sin((90 -\alpha) - \beta)$$= \sin (90- \alpha) \cos (\beta) - \sin ( \beta) \cos (90- \alpha)$

$=\cos \alpha \cos \beta - \sin \beta \sin \alpha$

Double Angle Identities

Double angle identities are easily derived from the angle addition formulas by just letting $\alpha = \beta$. Doing so yields:

$\sin 2\alpha =$2\sin \alpha \cos \alpha$$ (Error compiling LaTeX. Unknown error_msg)\cos 2\alpha = \cos^2 \alpha - \sin^2 \alpha$$ (Error compiling LaTeX. Unknown error_msg)=2\cos^2 \alpha - 1$$ (Error compiling LaTeX. Unknown error_msg)=1-2\sin^2 \alpha$$ (Error compiling LaTeX. Unknown error_msg)\tan 2\alpha $|| = ||$\frac{2\tan \alpha}{1-\tan^2\alpha} $== Half Angle Identities == Using the double angle identities, we can now derive half angle identities. The double angle formula for cosine tells us$\cos 2\alpha = 2\cos^2 \alpha - 1 $. Solving for$\cos \alpha $we get$\cos \alpha =\pm \sqrt{\frac{1 + \cos 2\alpha}2}$where we look at the quadrant of$\alpha $to decide if it's positive or negative. Likewise, we can use the fact that$\cos 2\alpha = 1 - 2\sin^2 \alpha $to find a half angle identity for sine. Then, to find a half angle identity for tangent, we just use the fact that$\tan \frac x2 =\frac{\sin \frac x2}{\cos \frac x2} $and plug in the half angle identities for sine and cosine.

To summarize:$ (Error compiling LaTeX. Unknown error_msg) \sin \frac{\theta}2 = \pm \sqrt{\frac{1-\cos \theta}2} $$ (Error compiling LaTeX. Unknown error_msg) \cos \frac{\theta}2 = \pm \sqrt{\frac{1+\cos \theta}2} $$ (Error compiling LaTeX. Unknown error_msg) \tan \frac{\theta}2 = \pm \sqrt{\frac{1-\cos \theta}{1+\cos \theta}} $== Even-Odd Identities ==$\sin (-\theta) = -\sin (\theta) $$ (Error compiling LaTeX. Unknown error_msg)\cos (-\theta) = \cos (\theta) $$ (Error compiling LaTeX. Unknown error_msg)\tan (-\theta) = -\tan (\theta) $$ (Error compiling LaTeX. Unknown error_msg)\csc (-\theta) = -\csc (\theta) $$ (Error compiling LaTeX. Unknown error_msg)\sec (-\theta) = \sec (\theta) $$ (Error compiling LaTeX. Unknown error_msg)\cot (-\theta) = -\cot (\theta) $==Prosthaphaeresis Identities== (Otherwise known as sum-to-product identities)

  • $ (Error compiling LaTeX. Unknown error_msg)\sin \theta \pm \sin \gamma = 2 \sin \frac{\theta\pm \gamma}2 \cos \frac{\theta\mp \gamma}2$*$\cos \theta + \cos \gamma = 2 \cos \frac{\theta+\gamma}2 \cos \frac{\theta-\gamma}2$*$\cos \theta - \cos \gamma = -2 \sin \frac{\theta+\gamma}2 \sin \frac{\theta-\gamma}2$== Law of Sines ==

{{main|Law of Sines}} The extended [[Law of Sines]] states

  • $ (Error compiling LaTeX. Unknown error_msg)\frac a{\sin A} = \frac b{\sin B} = \frac c{\sin C} = 2R.$== Law of Cosines ==

{{main|Law of Cosines}} The [[Law of Cosines]] states

  • $ (Error compiling LaTeX. Unknown error_msg)a^2 = b^2 + c^2 - 2bc\cos A. $== Law of Tangents ==

{{main|Law of Tangents}} The [[Law of Tangents]] states

  • $ (Error compiling LaTeX. Unknown error_msg)\frac{b - c}{b + c} = \frac{\tan\frac 12(B-C)}{\tan \frac 12(B+C)}.$== Other Identities = *$|1-e^{i\theta}|=2\sin\frac{\theta}{2}$

See also

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Trigonometric_identities&oldid=18717"