Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2023 AMC 8 Problems/Problem 13"

(Made the variable definition clearer, and reformatted the solution.)
(Made the variable definition clearer, and reformatted the solution.)
Line 10: Line 10:
 
==Solution==
 
==Solution==
  
 +
Suppose that the race is <math>d</math> miles long. The water stations are located at <cmath>\frac{d}{8}, \frac{2d}{8}, \ldots, \frac{7d}{8}</cmath> miles from the start, and the repair stations are located at <cmath>\frac{d}{3}, \frac{2d}{3}</cmath> miles from the start.
  
−
 
+
We are given that <math>\frac{3d}{8}=\frac{d}{3}+2,</math> from which 
−
Knowing that there are <math>7</math> equally spaced water stations they are each located <math>\frac{d}{8}</math>, <math>\frac{2d}{8}</math>,… <math>\frac{7d}{8}</math> of the way from the start. Using the same logic for the <math>3</math> station we have <math>\frac{d}{3}</math> and <math>\frac{2d}{3}</math> for the repair stations. It is given that the 3rd water is <math>2</math> miles ahead of the <math>1</math>st repair station. So setting an equation we have <math>\frac{3d}{8} = \frac{d}{3} + 2</math> getting common denominators <math>\frac{9d}{24} = \frac{8d}{24} + 2</math> so then we have <math>d = \boxed{\text{(D)}~48}</math> from this.
+
<cmath>\begin{align*}
−
 
+
\frac{9d}{24}&=\frac{8d}{24}+2 \\
 +
\frac{d}{24}&=2 \\
 +
d&=\boxed{\textbf{(D)}\ 48}.
 +
\end{align*}</cmath>
 
~apex304, SohumUttamchandani, wuwang2002, TaeKim, Cxrupptedpat, MRENTHUSIASM
 
~apex304, SohumUttamchandani, wuwang2002, TaeKim, Cxrupptedpat, MRENTHUSIASM
  

Revision as of 16:27, 25 January 2023

Problem

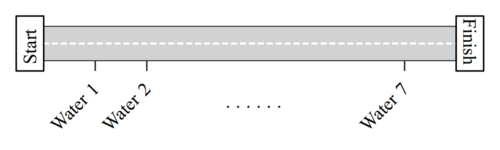
Along the route of a bicycle race, $7$ water stations are evenly spaced between the start and finish lines, as shown in the figure below. There are also $2$ repair stations evenly spaced between the start and finish lines. The $3$rd water station is located $2$ miles after the $1$st repair station. How long is the race in miles?

2023 AMC 8-13.png

$\textbf{(A)}\ 8 \qquad \textbf{(B)}\ 16 \qquad \textbf{(C)}\ 24 \qquad \textbf{(D)}\ 48 \qquad \textbf{(E)}\ 96$

Solution

Suppose that the race is $d$ miles long. The water stations are located at \[\frac{d}{8}, \frac{2d}{8}, \ldots, \frac{7d}{8}\] miles from the start, and the repair stations are located at \[\frac{d}{3}, \frac{2d}{3}\] miles from the start.

We are given that $\frac{3d}{8}=\frac{d}{3}+2,$ from which \begin{align*} \frac{9d}{24}&=\frac{8d}{24}+2 \\ \frac{d}{24}&=2 \\ d&=\boxed{\textbf{(D)}\ 48}. \end{align*} ~apex304, SohumUttamchandani, wuwang2002, TaeKim, Cxrupptedpat, MRENTHUSIASM

Video Solution (Animated)

https://youtu.be/NivfOThj1No

~Star League (https://starleague.us)

Video Solution by Magic Square

https://youtu.be/-N46BeEKaCQ?t=4439

See Also

2023 AMC 8 (Problems • Answer Key • Resources)
Preceded by
Problem 12 		Followed by
Problem 14
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AJHSME/AMC 8 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2023_AMC_8_Problems/Problem_13&oldid=187963"