Difference between revisions of "2024 AMC 8 Problems/Problem 6"
(→Problem) |
m (→Solution 1) |
||
| (34 intermediate revisions by 16 users not shown) | |||
| Line 1: | Line 1: | ||
==Problem== | ==Problem== | ||
| − | |||
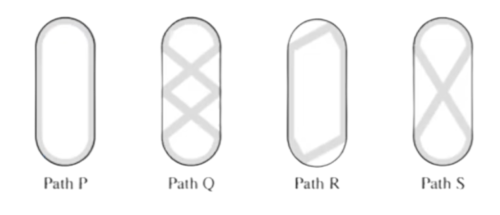
| − | (A) | + | Sergai skated around an ice rink, gliding along different paths. The gray lines in the figures below show four of the paths labeled P, Q, R, and S. What is the sorted order of the four paths from shortest to longest? |
| − | + | ||
| − | + | [[Image:2024_AMC_8-Problem_6.png|500px]] | |
| + | |||
| + | <math>\textbf{(A)}\ P,Q,R,S \qquad \textbf{(B)}\ P,R,S,Q \qquad \textbf{(C)}\ Q,S,P,R \qquad \textbf{(D)}\ R,P,S,Q \qquad \textbf{(E)}\ R,S,P,Q</math> | ||
==Solution 1== | ==Solution 1== | ||
| + | |||
| + | You can measure the lengths of the paths until you find a couple of guaranteed true inferred statements as such: | ||
| + | Q is greater than S, | ||
| + | P is greater than R, | ||
| + | and R and P are the smallest two, therefore the order is R, P, S, Q. | ||
| + | Thus we get the answer (D) R, P, S, Q | ||
| + | |||
| + | - U-King | ||
| + | |||
| + | ==Solution 2 (Intuitive)== | ||
| + | |||
| + | Obviously Path Q is the longest path, followed by Path S. | ||
| + | |||
| + | So, it is down to Paths P and R. | ||
| + | |||
| + | Notice that curved lines are always longer than the straight ones that meet their endpoints, therefore Path P is longer than Path R. | ||
| + | |||
| + | Thus, the order from shortest to longest is <math>\boxed{\textbf{(D) } \text{R, P, S, Q}}</math>. | ||
| + | |||
| + | ~MrThinker | ||
| + | |||
| + | ==Video Solution 1 by NiuniuMaths (Easy to understand!)== | ||
| + | https://www.youtube.com/watch?v=V-xN8Njd_Lc | ||
| + | |||
| + | ~NiuniuMaths | ||
| + | |||
| + | |||
| + | ==Video Solution by Math-X (First fully understand the problem!!!)== | ||
| + | https://youtu.be/BaE00H2SHQM?si=ZedvqIYTDG3D20Rp&t=1301 | ||
| + | |||
| + | ~Math-X | ||
| + | |||
| + | ==Video Solution by Power Solve (easy to digest!)== | ||
| + | https://www.youtube.com/watch?v=16YYti_pDUg | ||
| + | |||
| + | ==Video Solution by Interstigation== | ||
| + | https://youtu.be/ktzijuZtDas&t=386 | ||
| + | |||
| + | ==See Also== | ||
| + | {{AMC8 box|year=2024|num-b=5|num-a=7}} | ||
| + | {{MAA Notice}} | ||
Revision as of 09:41, 19 February 2024
Contents
Problem
Sergai skated around an ice rink, gliding along different paths. The gray lines in the figures below show four of the paths labeled P, Q, R, and S. What is the sorted order of the four paths from shortest to longest?
![]()
Solution 1
You can measure the lengths of the paths until you find a couple of guaranteed true inferred statements as such: Q is greater than S, P is greater than R, and R and P are the smallest two, therefore the order is R, P, S, Q. Thus we get the answer (D) R, P, S, Q
- U-King
Solution 2 (Intuitive)
Obviously Path Q is the longest path, followed by Path S.
So, it is down to Paths P and R.
Notice that curved lines are always longer than the straight ones that meet their endpoints, therefore Path P is longer than Path R.
Thus, the order from shortest to longest is ![]() .
.
~MrThinker
Video Solution 1 by NiuniuMaths (Easy to understand!)
https://www.youtube.com/watch?v=V-xN8Njd_Lc
~NiuniuMaths
Video Solution by Math-X (First fully understand the problem!!!)
https://youtu.be/BaE00H2SHQM?si=ZedvqIYTDG3D20Rp&t=1301
~Math-X
Video Solution by Power Solve (easy to digest!)
https://www.youtube.com/watch?v=16YYti_pDUg
Video Solution by Interstigation
https://youtu.be/ktzijuZtDas&t=386
See Also
| 2024 AMC 8 (Problems • Answer Key • Resources) | ||
| Preceded by Problem 5 |
Followed by Problem 7 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AJHSME/AMC 8 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.