Difference between revisions of "2024 AMC 8 Problems"
(→Problem 22) |
m (→Problem 17) |
||
| (26 intermediate revisions by 6 users not shown) | |||
| Line 54: | Line 54: | ||
<math>\textbf{(A) } 5\qquad\textbf{(B) } 6\qquad\textbf{(C) } 7\qquad\textbf{(D) } 8\qquad\textbf{(E) } 9</math> | <math>\textbf{(A) } 5\qquad\textbf{(B) } 6\qquad\textbf{(C) } 7\qquad\textbf{(D) } 8\qquad\textbf{(E) } 9</math> | ||
| + | |||
[[2024 AMC 8 Problems/Problem 4|Solution]] | [[2024 AMC 8 Problems/Problem 4|Solution]] | ||
| Line 67: | Line 68: | ||
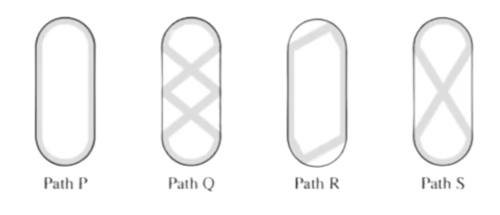
Sergei skated around an ice rink, gliding along different paths. The gray lines in the figures below show four of the paths labeled <math>P</math>, <math>Q</math>, <math>R</math>, and <math>S.</math> What is the sorted order of the four paths from shortest to longest? | Sergei skated around an ice rink, gliding along different paths. The gray lines in the figures below show four of the paths labeled <math>P</math>, <math>Q</math>, <math>R</math>, and <math>S.</math> What is the sorted order of the four paths from shortest to longest? | ||
| + | |||
| + | [[Image:2024_AMC_8-Problem_6.png|center|500px]] | ||
<math>\textbf{(A)}\ P,Q,R,S \qquad \textbf{(B)}\ P,R,S,Q \qquad \textbf{(C)}\ Q,S,P,R \qquad \textbf{(D)}\ R,P,S,Q \qquad \textbf{(E)}\ R,S,P,Q</math> | <math>\textbf{(A)}\ P,Q,R,S \qquad \textbf{(B)}\ P,R,S,Q \qquad \textbf{(C)}\ Q,S,P,R \qquad \textbf{(D)}\ R,P,S,Q \qquad \textbf{(E)}\ R,S,P,Q</math> | ||
| Line 82: | Line 85: | ||
==Problem 8== | ==Problem 8== | ||
| − | On Monday Taye has \$2. Every day, he either gains \$3 or doubles the amount of money he had on the previous day. How many different dollar amounts could Taye have on Thursday, 3 days later? | + | On Monday Taye has <math>\$2</math>. Every day, he either gains <math>\$3</math> or doubles the amount of money he had on the previous day. How many different dollar amounts could Taye have on Thursday, <math>3</math> days later? |
<math>\textbf{(A) } 3\qquad\textbf{(B) } 4\qquad\textbf{(C) } 5\qquad\textbf{(D) } 6\qquad\textbf{(E) } 7</math> | <math>\textbf{(A) } 3\qquad\textbf{(B) } 4\qquad\textbf{(C) } 5\qquad\textbf{(D) } 6\qquad\textbf{(E) } 7</math> | ||
| Line 149: | Line 152: | ||
(For example, one sequence of hops is up-up-down-down-up-down.) | (For example, one sequence of hops is up-up-down-down-up-down.) | ||
| − | + | <asy> | |
| + | /* AMC8 P13 2024, revised by Teacher David */ | ||
| + | /** | ||
| + | * This Geometry Artwork/Graph is designed using GeoSketch v1.0, | ||
| + | * a free software tool created by Tina Yan, William Zhong, and | ||
| + | * Teacher David. | ||
| + | * | ||
| + | * For more information, please refer to | ||
| + | * https://geosketch.org (under construction) | ||
| + | */ | ||
| + | defaultpen(linewidth(1pt)); | ||
| + | unitsize(0.3pt); | ||
| + | import graph; | ||
| + | /** | ||
| + | * Define a quadratic bezier curve function. | ||
| + | */ | ||
| + | typedef pair quad_bezier(real t); | ||
| + | quad_bezier fungen (pair a, pair b, pair c) { | ||
| + | return new pair (real t) { | ||
| + | real x = (1-t)*(1-t)*a.x + 2*(1-t)*t*b.x + t*t*c.x; | ||
| + | real y = (1-t)*(1-t)*a.y + 2*(1-t)*t*b.y + t*t*c.y; | ||
| + | return (x,y); | ||
| + | }; | ||
| + | } | ||
| + | |||
| + | quad_bezier qb0 = fungen((293,243),(237,276),(239,310)); | ||
| + | draw(graph(qb0, 0,1)); | ||
| + | quad_bezier qb1 = fungen((239,310),(274,301),(295,254)); | ||
| + | draw(graph(qb1, 0,1)); | ||
| + | quad_bezier qb2 = fungen((266,294),(260,309),(266,323)); | ||
| + | draw(graph(qb2, 0,1)); | ||
| + | quad_bezier qb3 = fungen((266,323),(294,311),(302,257)); | ||
| + | draw(graph(qb3, 0,1)); | ||
| + | quad_bezier qb4 = fungen((333,258),(341,249),(348,244)); | ||
| + | draw(graph(qb4, 0,1)); | ||
| + | quad_bezier qb5 = fungen((348,244),(355,241),(351,234)); | ||
| + | draw(graph(qb5, 0,1)); | ||
| + | quad_bezier qb6 = fungen((351,234),(348,226),(338,226)); | ||
| + | draw(graph(qb6, 0,1)); | ||
| + | quad_bezier qb7 = fungen((351,234),(350,219),(321,208)); | ||
| + | draw(graph(qb7, 0,1)); | ||
| + | quad_bezier qb8 = fungen((260,247),(135,293),(137,170)); | ||
| + | draw(graph(qb8, 0,1)); | ||
| + | quad_bezier qb9 = fungen((122,161),(132,147),(148,144)); | ||
| + | draw(graph(qb9, 0,1)); | ||
| + | quad_bezier qb10 = fungen((148,144),(176,155),(204,146)); | ||
| + | draw(graph(qb10, 0,1)); | ||
| + | quad_bezier qb11 = fungen((204,146),(216,141),(235,137)); | ||
| + | draw(graph(qb11, 0,1)); | ||
| + | quad_bezier qb12 = fungen((228,156),(208,160),(188,161)); | ||
| + | draw(graph(qb12, 0,1)); | ||
| + | quad_bezier qb13 = fungen((319,214),(313,174),(283,168)); | ||
| + | draw(graph(qb13, 0,1)); | ||
| + | quad_bezier qb14 = fungen((228,156),(242,158),(247,171)); | ||
| + | draw(graph(qb14, 0,1)); | ||
| + | quad_bezier qb15 = fungen((245,181),(250,158),(266,143)); | ||
| + | draw(graph(qb15, 0,1)); | ||
| + | quad_bezier qb16 = fungen((266,143),(287,134),(298,135)); | ||
| + | draw(graph(qb16, 0,1)); | ||
| + | quad_bezier qb17 = fungen((298,135),(309,143),(300,148)); | ||
| + | draw(graph(qb17, 0,1)); | ||
| + | quad_bezier qb18 = fungen((300,148),(272,150),(270,175)); | ||
| + | draw(graph(qb18, 0,1)); | ||
| + | quad_bezier qb19 = fungen((282,177),(274,158),(300,148)); | ||
| + | draw(graph(qb19, 0,1)); | ||
| + | |||
| + | draw(arc((317.8948497854077,245.25965665236052), 19.760615163024095, 143.54947493250435, 40.14574559948477)); | ||
| + | draw(arc((282.65584415584414,295.7857142857143), 53.78971270402217, -78.91253214600312, -114.90992209204622)); | ||
| + | draw(arc((127.7,168.5), 9.420191080864546, 9.162347045721713, 232.7651660184253)); | ||
| + | draw(arc((229.125,145.625), 10.435815732370902, -55.73889710090544, 96.1886159632416)); | ||
| + | draw(arc((186.26470588235293,181.5), 20.573313920580237, -85.1615330431756, 85.1615330431756)); | ||
| + | filldraw(ellipse((314,235), 13.0, 10.04987562112089), rgb(254,255,255), black); | ||
| + | filldraw(rotate(14.036243467926468,(315,251))*ellipse((315,235), 9.219544457292887, 8.246211251235321), | ||
| + | rgb(0,0,0), black); | ||
| + | |||
| + | pair o = (400,190); | ||
| + | real len=80; | ||
| + | real height=56; | ||
| + | for (int i=0; i<4; ++i) { | ||
| + | pair a = (i*len, i*height); | ||
| + | path p = a -- a+(len,0) -- a+(len, height); | ||
| + | draw(shift(o)*p); | ||
| + | } | ||
| + | path p = (0,0)--(0,-height)--(4*len,-height); | ||
| + | draw(shift(o)*p); | ||
| + | </asy> | ||
| Line 185: | Line 273: | ||
==Problem 17== | ==Problem 17== | ||
| − | A chess king is said to ''attack'' all squares one step away from it, horizontally, vertically, or diagonally. For instance, a king on the center square of a 3 x 3 grid attacks all 8 other squares, as shown below. Suppose a white king and a black king are placed on different squares of 3 x 3 grid so that they do not attack each other. In how many ways can this be done? | + | A chess king is said to ''attack'' all squares one step away from it (basically any square right next to it in any direction), horizontally, vertically, or diagonally. For instance, a king on the center square of a 3 x 3 grid attacks all 8 other squares, as shown below. Suppose a white king and a black king are placed on different squares of 3 x 3 grid so that they do not attack each other. In how many ways can this be done? |
<asy> | <asy> | ||
| Line 286: | Line 374: | ||
==Problem 22== | ==Problem 22== | ||
| − | A roll of tape is 4 inches in diameter and is wrapped around a ring that is 2 inches in diameter. A cross section of the tape is shown in the figure below. The tape is 0.015 inches thick. If the tape is completely unrolled, approximately how long would it be? Round your answer to the nearest 100 inches. | + | A roll of tape is <math>4</math> inches in diameter and is wrapped around a ring that is <math>2</math> inches in diameter. A cross section of the tape is shown in the figure below. The tape is <math>0.015</math> inches thick. If the tape is completely unrolled, approximately how long would it be? Round your answer to the nearest <math>100</math> inches. |
<asy> | <asy> | ||
| Line 389: | Line 477: | ||
A small airplane has <math>4</math> rows of seats with <math>3</math> seats in each row. Eight passengers have boarded the plane and are distributed randomly among the seats. A married couple is next to board. What is the probability there will be <math>2</math> adjacent seats in the same row for the couple? | A small airplane has <math>4</math> rows of seats with <math>3</math> seats in each row. Eight passengers have boarded the plane and are distributed randomly among the seats. A married couple is next to board. What is the probability there will be <math>2</math> adjacent seats in the same row for the couple? | ||
| − | [ | + | [[Image:2024_AMC_8-Problem_25.png|center|150px]] |
<math>\textbf{(A)}\ \dfrac{8}{15} \qquad \textbf{(B)}\ \dfrac{32}{55} \qquad \textbf{(C)}\ \dfrac{20}{33} \qquad \textbf{(D)}\ \dfrac{34}{55} \qquad \textbf{(E)}\ \dfrac{8}{11}</math> | <math>\textbf{(A)}\ \dfrac{8}{15} \qquad \textbf{(B)}\ \dfrac{32}{55} \qquad \textbf{(C)}\ \dfrac{20}{33} \qquad \textbf{(D)}\ \dfrac{34}{55} \qquad \textbf{(E)}\ \dfrac{8}{11}</math> | ||
Revision as of 16:51, 8 May 2024
| 2024 AMC 8 (Answer Key) Printable versions: • AoPS Resources • PDF | ||
|
Instructions
| ||
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
Contents
- 1 Problem 1
- 2 Problem 2
- 3 Problem 3
- 4 Problem 4
- 5 Problem 5
- 6 Problem 6
- 7 Problem 7
- 8 Problem 8
- 9 Problem 9
- 10 Problem 10
- 11 Problem 11
- 12 Problem 12
- 13 Problem 13
- 14 Problem 14
- 15 Problem 15
- 16 Problem 16
- 17 Problem 17
- 18 Problem 18
- 19 Problem 19
- 20 Problem 20
- 21 Problem 21
- 22 Problem 22
- 23 Problem 23
- 24 Problem 24
- 25 Problem 25
- 26 See Also
Problem 1
What is the ones digit of ![]()
![]()
Problem 2
What is the value of this expression in decimal form?
![]()
![]()
Problem 3
Four squares of side lengths ![]() ,
, ![]() ,
, ![]() , and
, and ![]() units are arranged in increasing size order so that their left edges and bottom edges align. The squares alternate in the color pattern white-gray-white-gray, respectively, as shown in the figure. What is the area of the visible gray region in square units?
units are arranged in increasing size order so that their left edges and bottom edges align. The squares alternate in the color pattern white-gray-white-gray, respectively, as shown in the figure. What is the area of the visible gray region in square units?
![[asy] size(150); filldraw((0,0)--(10,0)--(10,10)--(0,10)--cycle,gray(0.7),linewidth(1)); filldraw((0,0)--(9,0)--(9,9)--(0,9)--cycle,white,linewidth(1)); filldraw((0,0)--(7,0)--(7,7)--(0,7)--cycle,gray(0.7),linewidth(1)); filldraw((0,0)--(4,0)--(4,4)--(0,4)--cycle,white,linewidth(1)); draw((11,0)--(11,4),linewidth(1)); draw((11,6)--(11,10),linewidth(1)); label("$10$",(11,5),fontsize(14pt)); draw((10.75,0)--(11.25,0),linewidth(1)); draw((10.75,10)--(11.25,10),linewidth(1)); draw((0,11)--(4,11),linewidth(1)); draw((6,11)--(9,11),linewidth(1)); draw((0,11.25)--(0,10.75),linewidth(1)); draw((9,11.25)--(9,10.75),linewidth(1)); label("$9$",(5,11),fontsize(14pt)); draw((-1,0)--(-1,1),linewidth(1)); draw((-1,3)--(-1,7),linewidth(1)); draw((-1.25,0)--(-0.75,0),linewidth(1)); draw((-1.25,7)--(-0.75,7),linewidth(1)); label("$7$",(-1,2),fontsize(14pt)); draw((0,-1)--(1,-1),linewidth(1)); draw((3,-1)--(4,-1),linewidth(1)); draw((0,-1.25)--(0,-.75),linewidth(1)); draw((4,-1.25)--(4,-.75),linewidth(1)); label("$4$",(2,-1),fontsize(14pt)); [/asy]](http://latex.artofproblemsolving.com/5/e/6/5e6ea6522b82628aaadddaea887d0fa38d9bd19d.png)
![]()
Problem 4
When Yunji added all the integers from ![]() to
to ![]() , she mistakenly left out a number. Her incorrect sum turned out to be a square number. What number did Yunji leave out?
, she mistakenly left out a number. Her incorrect sum turned out to be a square number. What number did Yunji leave out?
![]()
Problem 5
Aaliyah rolls two standard 6-sided dice. She notices that the product of the two numbers rolled is a multiple of ![]() . Which of the following integers cannot be the sum of the two numbers?
. Which of the following integers cannot be the sum of the two numbers?
![]()
Problem 6
Sergei skated around an ice rink, gliding along different paths. The gray lines in the figures below show four of the paths labeled ![]() ,
, ![]() ,
, ![]() , and
, and ![]() What is the sorted order of the four paths from shortest to longest?
What is the sorted order of the four paths from shortest to longest?
![]()
Problem 7
A ![]() rectangle is covered without overlap by 3 shapes of tiles:
rectangle is covered without overlap by 3 shapes of tiles: ![]() ,
, ![]() , and
, and ![]() , shown below. What is the minimum possible number of
, shown below. What is the minimum possible number of ![]() tiles used?
tiles used?
![]()
Problem 8
On Monday Taye has ![]() . Every day, he either gains
. Every day, he either gains ![]() or doubles the amount of money he had on the previous day. How many different dollar amounts could Taye have on Thursday,
or doubles the amount of money he had on the previous day. How many different dollar amounts could Taye have on Thursday, ![]() days later?
days later?
![]()
Problem 9
All the marbles in Maria's collection are red, green, or blue. Maria has half as many red marbles as green marbles and twice as many blue marbles as green marbles. Which of the following could be the total number of marbles in Maria's collection?
![]()
Problem 10
In January 1980 the Moana Loa Observation recorded carbon dioxide ![]() levels of 338 ppm (parts per million). Over the years the average
levels of 338 ppm (parts per million). Over the years the average ![]() reading has increased by about 1.515 ppm each year. What is the expected
reading has increased by about 1.515 ppm each year. What is the expected ![]() level in ppm in January 2030? Round your answer to the nearest integer.
level in ppm in January 2030? Round your answer to the nearest integer.
![]()
Problem 11
The coordinates of ![]() are
are ![]() ,
, ![]() , and
, and ![]() , with
, with ![]() . The area of
. The area of ![]() is 12. What is the value of
is 12. What is the value of ![]() ?
?
![[asy] // Diagram inaccurate to prevent measuring with ruler. size(10cm); draw((3,10)--(11,7)--(5,7)--(3,10)); dot((5,7)); label("$A(5,7)$",(5,7),S); dot((11,7)); label("$B(11,7)$",(11,7),S); dot((3,10)); label("$C(3,y)$",(3,10),NW); // Problem 11: put on here by Andrei.martynau [/asy]](http://latex.artofproblemsolving.com/d/f/9/df9bdd320c29fe6940d579c3a338d6409290e950.png)
![]()
Problem 12
Rohan keeps a total of ![]() guppies in
guppies in ![]() fish tanks.
fish tanks.
- There is
 more guppy in the
more guppy in the  nd tank than the
nd tank than the  st tank.
st tank.
- There are
 more guppies in the 3rd tank than the
more guppies in the 3rd tank than the  nd tank.
nd tank.
- There are
 more guppies in the 4th tank than the
more guppies in the 4th tank than the  rd tank.
rd tank.
How many guppies are in the ![]() th tank?
th tank?
![]()
Problem 13
Buzz Bunny is hopping up and down a set of stairs, one step at a time. In how many ways can Buzz start on the ground, make a sequence of ![]() hops, and end up back on the ground?
(For example, one sequence of hops is up-up-down-down-up-down.)
hops, and end up back on the ground?
(For example, one sequence of hops is up-up-down-down-up-down.)
![[asy] /* AMC8 P13 2024, revised by Teacher David */ /** * This Geometry Artwork/Graph is designed using GeoSketch v1.0, * a free software tool created by Tina Yan, William Zhong, and * Teacher David. * * For more information, please refer to * https://geosketch.org (under construction) */ defaultpen(linewidth(1pt)); unitsize(0.3pt); import graph; /** * Define a quadratic bezier curve function. */ typedef pair quad_bezier(real t); quad_bezier fungen (pair a, pair b, pair c) { return new pair (real t) { real x = (1-t)*(1-t)*a.x + 2*(1-t)*t*b.x + t*t*c.x; real y = (1-t)*(1-t)*a.y + 2*(1-t)*t*b.y + t*t*c.y; return (x,y); }; } quad_bezier qb0 = fungen((293,243),(237,276),(239,310)); draw(graph(qb0, 0,1)); quad_bezier qb1 = fungen((239,310),(274,301),(295,254)); draw(graph(qb1, 0,1)); quad_bezier qb2 = fungen((266,294),(260,309),(266,323)); draw(graph(qb2, 0,1)); quad_bezier qb3 = fungen((266,323),(294,311),(302,257)); draw(graph(qb3, 0,1)); quad_bezier qb4 = fungen((333,258),(341,249),(348,244)); draw(graph(qb4, 0,1)); quad_bezier qb5 = fungen((348,244),(355,241),(351,234)); draw(graph(qb5, 0,1)); quad_bezier qb6 = fungen((351,234),(348,226),(338,226)); draw(graph(qb6, 0,1)); quad_bezier qb7 = fungen((351,234),(350,219),(321,208)); draw(graph(qb7, 0,1)); quad_bezier qb8 = fungen((260,247),(135,293),(137,170)); draw(graph(qb8, 0,1)); quad_bezier qb9 = fungen((122,161),(132,147),(148,144)); draw(graph(qb9, 0,1)); quad_bezier qb10 = fungen((148,144),(176,155),(204,146)); draw(graph(qb10, 0,1)); quad_bezier qb11 = fungen((204,146),(216,141),(235,137)); draw(graph(qb11, 0,1)); quad_bezier qb12 = fungen((228,156),(208,160),(188,161)); draw(graph(qb12, 0,1)); quad_bezier qb13 = fungen((319,214),(313,174),(283,168)); draw(graph(qb13, 0,1)); quad_bezier qb14 = fungen((228,156),(242,158),(247,171)); draw(graph(qb14, 0,1)); quad_bezier qb15 = fungen((245,181),(250,158),(266,143)); draw(graph(qb15, 0,1)); quad_bezier qb16 = fungen((266,143),(287,134),(298,135)); draw(graph(qb16, 0,1)); quad_bezier qb17 = fungen((298,135),(309,143),(300,148)); draw(graph(qb17, 0,1)); quad_bezier qb18 = fungen((300,148),(272,150),(270,175)); draw(graph(qb18, 0,1)); quad_bezier qb19 = fungen((282,177),(274,158),(300,148)); draw(graph(qb19, 0,1)); draw(arc((317.8948497854077,245.25965665236052), 19.760615163024095, 143.54947493250435, 40.14574559948477)); draw(arc((282.65584415584414,295.7857142857143), 53.78971270402217, -78.91253214600312, -114.90992209204622)); draw(arc((127.7,168.5), 9.420191080864546, 9.162347045721713, 232.7651660184253)); draw(arc((229.125,145.625), 10.435815732370902, -55.73889710090544, 96.1886159632416)); draw(arc((186.26470588235293,181.5), 20.573313920580237, -85.1615330431756, 85.1615330431756)); filldraw(ellipse((314,235), 13.0, 10.04987562112089), rgb(254,255,255), black); filldraw(rotate(14.036243467926468,(315,251))*ellipse((315,235), 9.219544457292887, 8.246211251235321), rgb(0,0,0), black); pair o = (400,190); real len=80; real height=56; for (int i=0; i<4; ++i) { pair a = (i*len, i*height); path p = a -- a+(len,0) -- a+(len, height); draw(shift(o)*p); } path p = (0,0)--(0,-height)--(4*len,-height); draw(shift(o)*p); [/asy]](http://latex.artofproblemsolving.com/a/5/9/a592633026df34caac63531f913a55032ce20311.png)
![]()
Problem 14
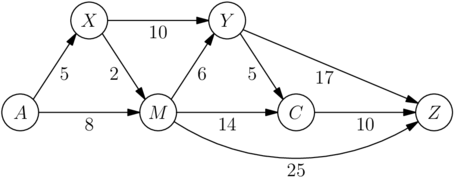
The one-way routes connecting towns ![]() and
and ![]() are shown in the figure below (not drawn to scale).The distances in kilometers along each route are marked. Traveling along these routes, what is the shortest distance from A to Z in kilometers?
are shown in the figure below (not drawn to scale).The distances in kilometers along each route are marked. Traveling along these routes, what is the shortest distance from A to Z in kilometers?
![]()
Problem 15
Let the letters ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() represent distinct digits. Suppose
represent distinct digits. Suppose ![]() is the greatest number that satisfies the equation
is the greatest number that satisfies the equation
![]()
What is the value of ![]() ?
?
![]()
Problem 16
Minh enters the numbers ![]() through
through ![]() into the cells of a
into the cells of a ![]() grid in some order. She calculates the product of the numbers in each row and column. What is the least number of rows and columns that could have a product divisible by
grid in some order. She calculates the product of the numbers in each row and column. What is the least number of rows and columns that could have a product divisible by ![]() ?
?
![]()
Problem 17
A chess king is said to attack all squares one step away from it (basically any square right next to it in any direction), horizontally, vertically, or diagonally. For instance, a king on the center square of a 3 x 3 grid attacks all 8 other squares, as shown below. Suppose a white king and a black king are placed on different squares of 3 x 3 grid so that they do not attack each other. In how many ways can this be done?
![[asy] /* AMC8 P17 2024, revised by Teacher David */ unitsize(29pt); import math; add(grid(3,3)); pair [] a = {(0.5,0.5), (0.5, 1.5), (0.5, 2.5), (1.5, 2.5), (2.5,2.5), (2.5,1.5), (2.5,0.5), (1.5,0.5)}; for (int i=0; i<a.length; ++i) { pair x = (1.5,1.5) + 0.4*dir(225-45*i); draw(x -- a[i], arrow=EndArrow()); } label("$K$", (1.5,1.5)); [/asy]](http://latex.artofproblemsolving.com/c/6/c/c6c43bfb745a1d180e54999f2ef50d6a26900b98.png)
![]()
Problem 18
Three concentric circles centered at ![]() have radii of
have radii of ![]() ,
, ![]() , and
, and ![]() . Points
. Points ![]() and
and ![]() lie on the largest circle. The region between the two smaller circles is shaded, as is the portion of the region between the two larger circles bounded by central angle
lie on the largest circle. The region between the two smaller circles is shaded, as is the portion of the region between the two larger circles bounded by central angle ![]() , as shown in the figure below. Suppose the shaded and unshaded regions are equal in area. What is the measure of
, as shown in the figure below. Suppose the shaded and unshaded regions are equal in area. What is the measure of ![]() in degrees?
in degrees?
![[asy] size(100); import graph; draw(circle((0,0),3)); real radius = 3; real angleStart = -54; // starting angle of the sector real angleEnd = 54; // ending angle of the sector label("$O$",(0,0),W); pair O = (0, 0); filldraw(arc(O, radius, angleStart, angleEnd)--O--cycle, lightgray); filldraw(circle((0,0),2),lightgray); filldraw(circle((0,0),1),white); draw((1.763,2.427)--(0,0)--(1.763,-2.427)); label("$B$",(1.763,2.427),NE); label("$C$",(1.763,-2.427),SE); [/asy]](http://latex.artofproblemsolving.com/4/0/a/40a568394360629541714ea7e47cf2d9cfde0edd.png)
![]()
Problem 19
Jordan owns 15 pairs of sneakers. Three fifths of the pairs are red and the rest are white. Two thirds of the pairs are high-top and the rest are low-top. The red high-top sneakers make up a fraction of the collection. What is the least possible value of this fraction?
![]()
Problem 20
Any three vertices of the cube ![]() shown in the figure below, can be connected to form a triangle.
shown in the figure below, can be connected to form a triangle. ![]() For example, vertices
For example, vertices ![]() and
and ![]() can be connected to form
can be connected to form ![]() How many of these triangles are equilateral and contain
How many of these triangles are equilateral and contain ![]() as a vertex?
as a vertex?
![[asy] unitsize(4); pair P,Q,R,S,T,U,V,W; P=(0,30); Q=(30,30); R=(40,40); S=(10,40); T=(10,10); U=(40,10); V=(30,0); W=(0,0); draw(W--V); draw(V--Q); draw(Q--P); draw(P--W); draw(T--U); draw(U--R); draw(R--S); draw(S--T); draw(W--T); draw(P--S); draw(V--U); draw(Q--R); dot(P); dot(Q); dot(R); dot(S); dot(T); dot(U); dot(V); dot(W); label("$P$",P,NW); label("$Q$",Q,NW); label("$R$",R,NE); label("$S$",S,N); label("$T$",T,NE); label("$U$",U,NE); label("$V$",V,SE); label("$W$",W,SW); [/asy]](http://latex.artofproblemsolving.com/4/b/c/4bc4c5b02dfaf07a435a3a5098a847d0af49d6c1.png)
![]()
Problem 21
A group of frogs (called an army) is living in a tree. A frog turns green when in the shade and turns yellow
when in the sun. Initially, the ratio of green to yellow frogs was ![]() . Then
. Then ![]() green frogs moved to the
sunny side and
green frogs moved to the
sunny side and ![]() yellow frogs moved to the shady side. Now the ratio is
yellow frogs moved to the shady side. Now the ratio is ![]() . What is the difference
between the number of green frogs and the number of yellow frogs now?
. What is the difference
between the number of green frogs and the number of yellow frogs now?
![]()
Problem 22
A roll of tape is ![]() inches in diameter and is wrapped around a ring that is
inches in diameter and is wrapped around a ring that is ![]() inches in diameter. A cross section of the tape is shown in the figure below. The tape is
inches in diameter. A cross section of the tape is shown in the figure below. The tape is ![]() inches thick. If the tape is completely unrolled, approximately how long would it be? Round your answer to the nearest
inches thick. If the tape is completely unrolled, approximately how long would it be? Round your answer to the nearest ![]() inches.
inches.
![[asy] /* AMC8 P22 2024, revised by Teacher David */ size(150); pair o = (0,0); real r1 = 1; real r2 = 2; filldraw(circle(o, r2), gray, linewidth(1pt)); filldraw(circle(o, r1), white, linewidth(1pt)); draw((-2,-2.6)--(-2,-2.4)); draw((2,-2.6)--(2,-2.4)); draw((-2,-2.5)--(2,-2.5), L=Label("4 in.")); draw((-1,0)--(1,0), L=Label("2 in.", align=(0,1)), arrow=Arrows()); draw((2,0)--(2,-1.3), linewidth(1pt)); [/asy]](http://latex.artofproblemsolving.com/7/f/0/7f0deaaf1b452b5a85b25daa299e496d57b8a91c.png)
![]()
Problem 23
Rodrigo has a very large sheet of graph paper. First he draws a line segment connecting point ![]() to point
to point ![]() and colors the
and colors the ![]() cells whose interiors intersect the segment, as shown below. Next Rodrigo draws a line segment connecting point
cells whose interiors intersect the segment, as shown below. Next Rodrigo draws a line segment connecting point ![]() to point
to point ![]() . How many cells will he color this time?
. How many cells will he color this time?
![[asy] filldraw((0,4)--(1,4)--(1,3)--(0,3)--cycle, gray(.75), gray(.5)+linewidth(1)); filldraw((0,3)--(1,3)--(1,2)--(0,2)--cycle, gray(.75), gray(.5)+linewidth(1)); filldraw((1,2)--(2,2)--(2,1)--(1,1)--cycle, gray(.75), gray(.5)+linewidth(1)); filldraw((1,1)--(2,1)--(2,0)--(1,0)--cycle, gray(.75), gray(.5)+linewidth(1)); draw((-1,5)--(-1,-1),gray(.9)); draw((0,5)--(0,-1),gray(.9)); draw((1,5)--(1,-1),gray(.9)); draw((2,5)--(2,-1),gray(.9)); draw((3,5)--(3,-1),gray(.9)); draw((4,5)--(4,-1),gray(.9)); draw((5,5)--(5,-1),gray(.9)); draw((-1,5)--(5, 5),gray(.9)); draw((-1,4)--(5,4),gray(.9)); draw((-1,3)--(5,3),gray(.9)); draw((-1,2)--(5,2),gray(.9)); draw((-1,1)--(5,1),gray(.9)); draw((-1,0)--(5,0),gray(.9)); draw((-1,-1)--(5,-1),gray(.9)); dot((0,4)); label("$(0,4)$",(0,4),NW); dot((2,0)); label("$(2,0)$",(2,0),SE); draw((0,4)--(2,0)); draw((-1,0) -- (5,0), arrow=Arrow); draw((0,-1) -- (0,5), arrow=Arrow); [/asy]](http://latex.artofproblemsolving.com/6/8/3/68329ca63ace9b040bb1d72663d99833fd645038.png)
![]()
Problem 24
Jean has made a piece of stained glass art in the shape of two mountains, as shown in the figure below. One mountain peak is ![]() feet high while the other peak is
feet high while the other peak is ![]() feet high. Each peak forms a
feet high. Each peak forms a ![]() angle, and the straight sides form a
angle, and the straight sides form a ![]() angle with the ground. The artwork has an area of
angle with the ground. The artwork has an area of ![]() square feet. The sides of the mountain meet at an intersection point near the center of the artwork,
square feet. The sides of the mountain meet at an intersection point near the center of the artwork, ![]() feet above the ground. What is the value of
feet above the ground. What is the value of ![]()
![[asy] unitsize(.3cm); filldraw((0,0)--(8,8)--(11,5)--(18,12)--(30,0)--cycle,gray(0.7),linewidth(1)); draw((-1,0)--(-1,8),linewidth(.75)); draw((-1.4,0)--(-.6,0),linewidth(.75)); draw((-1.4,8)--(-.6,8),linewidth(.75)); label("$8$",(-1,4),W); label("$12$",(31,6),E); draw((-1,8)--(8,8),dashed); draw((31,0)--(31,12),linewidth(.75)); draw((30.6,0)--(31.4,0),linewidth(.75)); draw((30.6,12)--(31.4,12),linewidth(.75)); draw((31,12)--(18,12),dashed); label("$45^{\circ}$",(.75,0),NE,fontsize(10pt)); label("$45^{\circ}$",(29.25,0),NW,fontsize(10pt)); draw((8,8)--(7.5,7.5)--(8,7)--(8.5,7.5)--cycle); draw((18,12)--(17.5,11.5)--(18,11)--(18.5,11.5)--cycle); draw((11,5)--(11,0),dashed); label("$h$",(11,2.5),E); [/asy]](http://latex.artofproblemsolving.com/0/6/2/062be4008fc995e68ebbe56afa0a90b07160a7d6.png)
![]()
Problem 25
A small airplane has ![]() rows of seats with
rows of seats with ![]() seats in each row. Eight passengers have boarded the plane and are distributed randomly among the seats. A married couple is next to board. What is the probability there will be
seats in each row. Eight passengers have boarded the plane and are distributed randomly among the seats. A married couple is next to board. What is the probability there will be ![]() adjacent seats in the same row for the couple?
adjacent seats in the same row for the couple?
![]()
See Also
| 2024 AMC 8 (Problems • Answer Key • Resources) | ||
| Preceded by 2023 AMC 8 |
Followed by 2025 AMC 8 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AJHSME/AMC 8 Problems and Solutions | ||