Difference between revisions of "2024 AMC 8 Problems/Problem 6"
(→Solution 1) (Tag: Blanking) |
Hsnacademy (talk | contribs) (→Video Solution 1 by NiuniuMaths (Easy to understand!)) |
||
| (34 intermediate revisions by 18 users not shown) | |||
| Line 1: | Line 1: | ||
| + | ==Problem== | ||
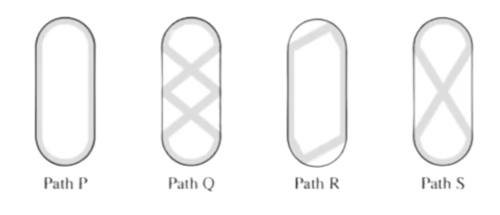
| + | Sergai skated around an ice rink, gliding along different paths. The gray lines in the figures below show four of the paths labeled P, Q, R, and S. What is the sorted order of the four paths from shortest to longest? | ||
| + | |||
| + | [[Image:2024_AMC_8-Problem_6.png|500px]] | ||
| + | |||
| + | <math>\textbf{(A)}\ P,Q,R,S \qquad \textbf{(B)}\ P,R,S,Q \qquad \textbf{(C)}\ Q,S,P,R \qquad \textbf{(D)}\ R,P,S,Q \qquad \textbf{(E)}\ R,S,P,Q</math> | ||
| + | |||
| + | ==Solution 1== | ||
| + | |||
| + | You can measure the lengths of the paths until you find a couple of guaranteed true inferred statements as such: | ||
| + | Q is greater than S, | ||
| + | P is greater than R, | ||
| + | and R and P are the smallest two, therefore the order is R, P, S, Q. | ||
| + | Thus we get the answer <math>\boxed{\textbf{(D)}~R, P, S, Q}</math>. | ||
| + | |||
| + | - U-King | ||
| + | |||
| + | ~ cxsmi (minor <math>\LaTeX</math> edits) | ||
| + | |||
| + | ==Solution 2 (Intuitive)== | ||
| + | |||
| + | Obviously Path Q is the longest path, followed by Path S. | ||
| + | |||
| + | So, it is down to Paths P and R. | ||
| + | |||
| + | Notice that curved lines are always longer than the straight ones that meet their endpoints, therefore Path P is longer than Path R. | ||
| + | |||
| + | Thus, the order from shortest to longest is <math>\boxed{\textbf{(D) } \text{R, P, S, Q}}</math>. | ||
| + | |||
| + | ~MrThinker | ||
| + | |||
| + | ==Video Solution (A Clever Explanation You’ll Get Instantly)== | ||
| + | https://youtu.be/5ZIFnqymdDQ?si=MmMWctYfzKIjwfE8&t=553 | ||
| + | |||
| + | ~hsnacademy | ||
| + | |||
| + | ==Video Solution 1 by NiuniuMaths (Easy to understand!)== | ||
| + | https://www.youtube.com/watch?v=V-xN8Njd_Lc | ||
| + | |||
| + | ~NiuniuMaths | ||
| + | |||
| + | ==Video Solution by Math-X (First fully understand the problem!!!)== | ||
| + | https://youtu.be/BaE00H2SHQM?si=ZedvqIYTDG3D20Rp&t=1301 | ||
| + | |||
| + | ~Math-X | ||
| + | |||
| + | ==Video Solution by Power Solve (easy to digest!)== | ||
| + | https://www.youtube.com/watch?v=16YYti_pDUg | ||
| + | |||
| + | ==Video Solution by Interstigation== | ||
| + | https://youtu.be/ktzijuZtDas&t=386 | ||
| + | |||
| + | ==Video Solution by Daily Dose of Math (Certified, Simple, and Logical)== | ||
| + | |||
| + | https://youtu.be/WJCwG6olgNU | ||
| + | |||
| + | ~Thesmartgreekmathdude | ||
| + | |||
| + | ==See Also== | ||
| + | {{AMC8 box|year=2024|num-b=5|num-a=7}} | ||
| + | {{MAA Notice}} | ||
Latest revision as of 20:26, 28 August 2024
Contents
- 1 Problem
- 2 Solution 1
- 3 Solution 2 (Intuitive)
- 4 Video Solution (A Clever Explanation You’ll Get Instantly)
- 5 Video Solution 1 by NiuniuMaths (Easy to understand!)
- 6 Video Solution by Math-X (First fully understand the problem!!!)
- 7 Video Solution by Power Solve (easy to digest!)
- 8 Video Solution by Interstigation
- 9 Video Solution by Daily Dose of Math (Certified, Simple, and Logical)
- 10 See Also
Problem
Sergai skated around an ice rink, gliding along different paths. The gray lines in the figures below show four of the paths labeled P, Q, R, and S. What is the sorted order of the four paths from shortest to longest?
![]()
Solution 1
You can measure the lengths of the paths until you find a couple of guaranteed true inferred statements as such:
Q is greater than S,
P is greater than R,
and R and P are the smallest two, therefore the order is R, P, S, Q.
Thus we get the answer ![]() .
.
- U-King
~ cxsmi (minor ![]() edits)
edits)
Solution 2 (Intuitive)
Obviously Path Q is the longest path, followed by Path S.
So, it is down to Paths P and R.
Notice that curved lines are always longer than the straight ones that meet their endpoints, therefore Path P is longer than Path R.
Thus, the order from shortest to longest is ![]() .
.
~MrThinker
Video Solution (A Clever Explanation You’ll Get Instantly)
https://youtu.be/5ZIFnqymdDQ?si=MmMWctYfzKIjwfE8&t=553
~hsnacademy
Video Solution 1 by NiuniuMaths (Easy to understand!)
https://www.youtube.com/watch?v=V-xN8Njd_Lc
~NiuniuMaths
Video Solution by Math-X (First fully understand the problem!!!)
https://youtu.be/BaE00H2SHQM?si=ZedvqIYTDG3D20Rp&t=1301
~Math-X
Video Solution by Power Solve (easy to digest!)
https://www.youtube.com/watch?v=16YYti_pDUg
Video Solution by Interstigation
https://youtu.be/ktzijuZtDas&t=386
Video Solution by Daily Dose of Math (Certified, Simple, and Logical)
~Thesmartgreekmathdude
See Also
| 2024 AMC 8 (Problems • Answer Key • Resources) | ||
| Preceded by Problem 5 |
Followed by Problem 7 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AJHSME/AMC 8 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.