Difference between revisions of "2006 AMC 10B Problems"
(accidentally changed <math> tags to $ signs) |
|||
| Line 1: | Line 1: | ||
== Problem 1 == | == Problem 1 == | ||
| − | What is | + | What is <math> (-1)^{1} + (-1)^{2} + ... + (-1)^{2006} </math> ? |
| − | + | <math> \mathrm{(A) \ } -2006\qquad \mathrm{(B) \ } -1\qquad \mathrm{(C) \ } 0\qquad \mathrm{(D) \ } 1\qquad \mathrm{(E) \ } 2006 </math> | |
[[2006 AMC 10B Problems/Problem 1|Solution]] | [[2006 AMC 10B Problems/Problem 1|Solution]] | ||
== Problem 2 == | == Problem 2 == | ||
| − | For real numbers | + | For real numbers <math>x</math> and <math>y</math>, define <math> x \spadesuit y = (x+y)(x-y) </math>. What is <math> 3 \spadesuit (4 \spadesuit 5) </math>? |
| − | + | <math> \mathrm{(A) \ } -72\qquad \mathrm{(B) \ } -27\qquad \mathrm{(C) \ } -24\qquad \mathrm{(D) \ } 24\qquad \mathrm{(E) \ } 72 </math> | |
[[2006 AMC 10B Problems/Problem 2|Solution]] | [[2006 AMC 10B Problems/Problem 2|Solution]] | ||
| Line 16: | Line 16: | ||
A football game was played between two teams, the Cougars and the Panthers. The two teams scored a total of 34 points, and the Cougars won by a margin of 14 points. How many points did the Panthers score? | A football game was played between two teams, the Cougars and the Panthers. The two teams scored a total of 34 points, and the Cougars won by a margin of 14 points. How many points did the Panthers score? | ||
| − | + | <math> \mathrm{(A) \ } 10\qquad \mathrm{(B) \ } 14\qquad \mathrm{(C) \ } 17\qquad \mathrm{(D) \ } 20\qquad \mathrm{(E) \ } 24 </math> | |
[[2006 AMC 10B Problems/Problem 3|Solution]] | [[2006 AMC 10B Problems/Problem 3|Solution]] | ||
| Line 25: | Line 25: | ||
[[Image:2006amc10b04.gif]] | [[Image:2006amc10b04.gif]] | ||
| − | + | <math> \mathrm{(A) \ } 2\qquad \mathrm{(B) \ } 3\qquad \mathrm{(C) \ } 6\qquad \mathrm{(D) \ } 8\qquad \mathrm{(E) \ } 9 </math> | |
[[2006 AMC 10B Problems/Problem 4|Solution]] | [[2006 AMC 10B Problems/Problem 4|Solution]] | ||
== Problem 5 == | == Problem 5 == | ||
| − | A | + | A <math> 2 \times 3 </math> rectangle and a <math> 3 \times 4 </math> rectangle are contained within a square without overlapping at any point, and the sides of the square are parallel to the sides of the two given rectangles. What is the smallest possible area of the square? |
| − | + | <math> \mathrm{(A) \ } 16\qquad \mathrm{(B) \ } 25\qquad \mathrm{(C) \ } 36\qquad \mathrm{(D) \ } 49\qquad \mathrm{(E) \ } 64 </math> | |
[[2006 AMC 10B Problems/Problem 5|Solution]] | [[2006 AMC 10B Problems/Problem 5|Solution]] | ||
== Problem 6 == | == Problem 6 == | ||
| − | A region is bounded by semicircular arcs constructed on the side of a square whose sides measure | + | A region is bounded by semicircular arcs constructed on the side of a square whose sides measure <math> \frac{2}{\pi} </math>, as shown. What is the perimeter of this region? |
[[Image:2006amc10b06.gif]] | [[Image:2006amc10b06.gif]] | ||
| − | + | <math> \mathrm{(A) \ } \frac{4}{\pi}\qquad \mathrm{(B) \ } 2\qquad \mathrm{(C) \ } \frac{8}{\pi}\qquad \mathrm{(D) \ } 4\qquad \mathrm{(E) \ } \frac{16}{\pi} </math> | |
[[2006 AMC 10B Problems/Problem 6|Solution]] | [[2006 AMC 10B Problems/Problem 6|Solution]] | ||
== Problem 7 == | == Problem 7 == | ||
| − | Which of the folowing is equivalent to | + | Which of the folowing is equivalent to <math> \sqrt{\frac{x}{1-\frac{x-1}{x}}} </math> when <math> x < 0 </math> |
| − | + | <math> \mathrm{(A) \ } -x\qquad \mathrm{(B) \ } x\qquad \mathrm{(C) \ } 1\qquad \mathrm{(D) \ } \sqrt{\frac{x}{2}}\qquad \mathrm{(E) \ } x\sqrt{-1} </math> | |
[[2006 AMC 10B Problems/Problem 7|Solution]] | [[2006 AMC 10B Problems/Problem 7|Solution]] | ||
| Line 57: | Line 57: | ||
[[Image:2006amc10b08.gif]] | [[Image:2006amc10b08.gif]] | ||
| − | + | <math> \mathrm{(A) \ } 20\pi\qquad \mathrm{(B) \ } 25\pi\qquad \mathrm{(C) \ } 30\pi\qquad \mathrm{(D) \ } 40\pi\qquad \mathrm{(E) \ } 50\pi </math> | |
[[2006 AMC 10B Problems/Problem 8|Solution]] | [[2006 AMC 10B Problems/Problem 8|Solution]] | ||
| Line 64: | Line 64: | ||
Francesca uses 100 grams of lemon juce, 100 grams of sugar, and 400 grams of water to make lemonade. There are 25 calories in 100 grams of lemon juice and 386 calories in 100 grams of sugar. Water contains no calories. How many calories are in 200 grams of her lemonade? | Francesca uses 100 grams of lemon juce, 100 grams of sugar, and 400 grams of water to make lemonade. There are 25 calories in 100 grams of lemon juice and 386 calories in 100 grams of sugar. Water contains no calories. How many calories are in 200 grams of her lemonade? | ||
| − | + | <math> \mathrm{(A) \ } 129\qquad \mathrm{(B) \ } 137\qquad \mathrm{(C) \ } 174\qquad \mathrm{(D) \ } 233\qquad \mathrm{(E) \ } 411 </math> | |
[[2006 AMC 10B Problems/Problem 9|Solution]] | [[2006 AMC 10B Problems/Problem 9|Solution]] | ||
| Line 71: | Line 71: | ||
In a triangle with integer side lengths, one side is three times as long as a second side, and the length of the third side is 15. What is the greatest possible perimeter of the triangle? | In a triangle with integer side lengths, one side is three times as long as a second side, and the length of the third side is 15. What is the greatest possible perimeter of the triangle? | ||
| − | + | <math> \mathrm{(A) \ } 43\qquad \mathrm{(B) \ } 44\qquad \mathrm{(C) \ } 45\qquad \mathrm{(D) \ } 46\qquad \mathrm{(E) \ } 47 </math> | |
[[2006 AMC 10B Problems/Problem 10|Solution]] | [[2006 AMC 10B Problems/Problem 10|Solution]] | ||
== Problem 11 == | == Problem 11 == | ||
| − | What is the tens digit in the sum | + | What is the tens digit in the sum <math> 7!+8!+9!+...+2006!</math> |
| − | + | <math> \mathrm{(A) \ } 1\qquad \mathrm{(B) \ } 3\qquad \mathrm{(C) \ } 4\qquad \mathrm{(D) \ } 6\qquad \mathrm{(E) \ } 9 </math> | |
[[2006 AMC 10B Problems/Problem 11|Solution]] | [[2006 AMC 10B Problems/Problem 11|Solution]] | ||
== Problem 12 == | == Problem 12 == | ||
| − | The lines | + | The lines <math> x=\frac{1}{4}y+a </math> and <math> y=\frac{1}{4}x+b </math> intersect at the point <math> (1,2) </math>. What is <math> a+b </math>? |
| − | + | <math> \mathrm{(A) \ } 0\qquad \mathrm{(B) \ } \frac{3}{4}\qquad \mathrm{(C) \ } 1\qquad \mathrm{(D) \ } 2\qquad \mathrm{(E) \ } \frac{9}{4} </math> | |
[[2006 AMC 10B Problems/Problem 12|Solution]] | [[2006 AMC 10B Problems/Problem 12|Solution]] | ||
| Line 92: | Line 92: | ||
Joe and JoAnn each bought 12 ounces of coffee in a 16 ounce cup. Joe drank 2 ounces of his coffee and then added 2 ounces of cream. JoAnn added 2 ounces of cream, stirred the coffee well, and then drank 2 ounces. What is the resulting ratio of the ammount of cream in Joe's coffee to that in JoAnn's coffee? | Joe and JoAnn each bought 12 ounces of coffee in a 16 ounce cup. Joe drank 2 ounces of his coffee and then added 2 ounces of cream. JoAnn added 2 ounces of cream, stirred the coffee well, and then drank 2 ounces. What is the resulting ratio of the ammount of cream in Joe's coffee to that in JoAnn's coffee? | ||
| − | + | <math> \mathrm{(A) \ } \frac{6}{7}\qquad \mathrm{(B) \ } \frac{13}{14}\qquad \mathrm{(C) \ }1 \qquad \mathrm{(D) \ } \frac{14}{13}\qquad \mathrm{(E) \ } \frac{7}{6} </math> | |
[[2006 AMC 10B Problems/Problem 13|Solution]] | [[2006 AMC 10B Problems/Problem 13|Solution]] | ||
== Problem 14 == | == Problem 14 == | ||
| − | Let | + | Let <math>a</math> and <math>b</math> be the roots of the equation <math> x^2-mx+2=0 </math>. Suppose that <math> a+(1/b) </math> and <math> b+(1/a) </math> are the roots of the equation <math> x^2-px+q=0 </math>. What is <math>q</math>? |
| − | + | <math> \mathrm{(A) \ } \frac{5}{2}\qquad \mathrm{(B) \ } \frac{7}{2}\qquad \mathrm{(C) \ } 4\qquad \mathrm{(D) \ } \frac{9}{2}\qquad \mathrm{(E) \ } 8 </math> | |
[[2006 AMC 10B Problems/Problem 14|Solution]] | [[2006 AMC 10B Problems/Problem 14|Solution]] | ||
== Problem 15 == | == Problem 15 == | ||
| − | Rhombus | + | Rhombus <math>ABCD</math> is similar to rhombus <math>BFDE</math>. The area of rhombus <math>ABCD</math> is <math>24</math> and <math> \angle BAD = 60^\circ </math>. What is the area of rhombus <math>BFDE</math>? |
[[Image:2006amc10b15.gif]] | [[Image:2006amc10b15.gif]] | ||
| − | + | <math> \mathrm{(A) \ } 6\qquad \mathrm{(B) \ } 4\sqrt{3}\qquad \mathrm{(C) \ } 8\qquad \mathrm{(D) \ } 9\qquad \mathrm{(E) \ } 6\sqrt{3} </math> | |
[[2006 AMC 10B Problems/Problem 15|Solution]] | [[2006 AMC 10B Problems/Problem 15|Solution]] | ||
| Line 115: | Line 115: | ||
Leap Day, February 29, 2004, occured on a Sunday. On what day of the week will Leap Day, February 29, 2020, occur? | Leap Day, February 29, 2004, occured on a Sunday. On what day of the week will Leap Day, February 29, 2020, occur? | ||
| − | + | <math> \mathrm{(A) \ } \textrm{Tuesday} \qquad \mathrm{(B) \ } \textrm{Wednesday} \qquad \mathrm{(C) \ } \textrm{Thursday} \qquad \mathrm{(D) \ } \textrm{Friday} \qquad \mathrm{(E) \ } \textrm{Saturday} </math> | |
[[2006 AMC 10B Problems/Problem 16|Solution]] | [[2006 AMC 10B Problems/Problem 16|Solution]] | ||
| Line 122: | Line 122: | ||
Bob and Alice each have a bag that contains one ball of each of the colors blue, green, orange, red, and violet. Alice randomly selects one ball from her bag and puts it into Bob's bag. Bob then randomly selects one ball from his bag and puts it into Alice's bag. What is the probability that after this process the contents of the two bags are the same? | Bob and Alice each have a bag that contains one ball of each of the colors blue, green, orange, red, and violet. Alice randomly selects one ball from her bag and puts it into Bob's bag. Bob then randomly selects one ball from his bag and puts it into Alice's bag. What is the probability that after this process the contents of the two bags are the same? | ||
| − | + | <math> \mathrm{(A) \ } \frac{1}{10}\qquad \mathrm{(B) \ } \frac{1}{6}\qquad \mathrm{(C) \ } \frac{1}{5}\qquad \mathrm{(D) \ } \frac{1}{3}\qquad \mathrm{(E) \ } \frac{1}{2} </math> | |
[[2006 AMC 10B Problems/Problem 17|Solution]] | [[2006 AMC 10B Problems/Problem 17|Solution]] | ||
== Problem 18 == | == Problem 18 == | ||
| − | Let | + | Let <math> a_1 , a_2 , ... </math> be a sequence for which |
| − | + | <math> a_1=2 </math> , <math> a_2=3 </math>, and <math>a_n=\frac{a_{n-1}}{a_{n-2}} </math> for each positive integer <math> n \ge 3 </math>. | |
| − | What is | + | What is <math> a_{2006} </math>? |
| − | + | <math> \mathrm{(A) \ } \frac{1}{2}\qquad \mathrm{(B) \ } \frac{2}{3}\qquad \mathrm{(C) \ } \frac{3}{2}\qquad \mathrm{(D) \ } 2\qquad \mathrm{(E) \ } 3 </math> | |
[[2006 AMC 10B Problems/Problem 18|Solution]] | [[2006 AMC 10B Problems/Problem 18|Solution]] | ||
== Problem 19 == | == Problem 19 == | ||
| − | A circle of radius | + | A circle of radius <math>2</math> is centered at <math>O</math>. Square <math>OABC</math> has side length <math>1</math>. Sides <math>AB</math> and <math>CB</math> are extended past <math>B</math> to meet the circle at <math>D</math> and <math>E</math>, respectively. What is the area of the shaded region in the figure, which is bounded by <math>BD</math>, <math>BE</math>, and the minor arc connecting <math>D</math> and <math>E</math>? |
[[Image:2006amc10b19.gif]] | [[Image:2006amc10b19.gif]] | ||
| − | + | <math> \mathrm{(A) \ } \frac{\pi}{3}+1-\sqrt{3}\qquad \mathrm{(B) \ } \frac{\pi}{2}(2-\sqrt{3})\qquad \mathrm{(C) \ } \pi(2-\sqrt{3})\qquad \mathrm{(D) \ } \frac{\pi}{6}+\frac{\sqrt{3}+1}{2}\qquad \mathrm{(E) \ } \frac{\pi}{3}-1+\sqrt{3} </math> | |
[[2006 AMC 10B Problems/Problem 19|Solution]] | [[2006 AMC 10B Problems/Problem 19|Solution]] | ||
== Problem 20 == | == Problem 20 == | ||
| − | In rectangle | + | In rectangle <math>ABCD</math>, we have <math>A=(6,-22)</math>, <math>B=(2006,178)</math>, <math>D=(8,y)</math>, for some integer <math>y</math>. What is the area of rectangle <math>ABCD</math>? |
| − | + | <math> \mathrm{(A) \ } 4000\qquad \mathrm{(B) \ } 4040\qquad \mathrm{(C) \ } 4400\qquad \mathrm{(D) \ } 40,000\qquad \mathrm{(E) \ } 40,400 </math> | |
[[2006 AMC 10B Problems/Problem 20|Solution]] | [[2006 AMC 10B Problems/Problem 20|Solution]] | ||
== Problem 21 == | == Problem 21 == | ||
| − | For a particular peculiar pair of dice, the probabilities of rolling | + | For a particular peculiar pair of dice, the probabilities of rolling <math>1</math>, <math>2</math>, <math>3</math>, <math>4</math>, <math>5</math>, and <math>6</math>, on each die are in the ratio <math>1:2:3:4:5:6</math>. What is the probability of rolling a total of <math>7</math> on the two dice? |
| − | + | <math> \mathrm{(A) \ } \frac{4}{63}\qquad \mathrm{(B) \ } \frac{1}{8}\qquad \mathrm{(C) \ } \frac{8}{63}\qquad \mathrm{(D) \ } \frac{1}{6}\qquad \mathrm{(E) \ } \frac{2}{7} </math> | |
[[2006 AMC 10B Problems/Problem 21|Solution]] | [[2006 AMC 10B Problems/Problem 21|Solution]] | ||
== Problem 22 == | == Problem 22 == | ||
| − | Elmo makes | + | Elmo makes <math>N</math> sandwiches for a fundraiser. For each sandwich he uses <math>B</math> globs of peanut butter at <math>4</math>¢ per glob and <math>J</math> blobs of jam at <math>5</math>¢ per blob. The cost of the peanut butter and jam to make all the sandwiches is <math>\$2.53</math>. Assume that <math>B</math>, <math>J</math>, and <math>N</math> are positive integers with <math>N>1</math>. What is the cost of the jam Elmo uses to make the sandwiches? |
| − | + | <math> \mathrm{(A) \ } 1.05\qquad \mathrm{(B) \ } 1.25\qquad \mathrm{(C) \ } 1.45\qquad \mathrm{(D) \ } 1.65\qquad \mathrm{(E) \ } 1.85 </math> | |
[[2006 AMC 10B Problems/Problem 22|Solution]] | [[2006 AMC 10B Problems/Problem 22|Solution]] | ||
| Line 172: | Line 172: | ||
[[Image:2006amc10b23.gif]] | [[Image:2006amc10b23.gif]] | ||
| − | + | <math> \mathrm{(A) \ } 15\qquad \mathrm{(B) \ } 17\qquad \mathrm{(C) \ } \frac{35}{2}\qquad \mathrm{(D) \ } 18\qquad \mathrm{(E) \ } \frac{55}{3} </math> | |
[[2006 AMC 10B Problems/Problem 23|Solution]] | [[2006 AMC 10B Problems/Problem 23|Solution]] | ||
== Problem 24 == | == Problem 24 == | ||
| − | Circles with centers | + | Circles with centers <math>O</math> and <math>P</math> have radii <math>2</math> and <math>4</math>, respectively, and are externally tangent. Points <math>A</math> and <math>B</math> on the circle with center <math>O</math> and points <math>C</math> and <math>D</math> on the circle with center <math>P</math> are such that <math>AD</math> and <math>BC</math> are common external tangents to the circles. What is the area of the concave hexagon <math>AOBCPD</math>? |
[[Image:2006amc10b24.gif]] | [[Image:2006amc10b24.gif]] | ||
| − | + | <math> \mathrm{(A) \ } 18\sqrt{3}\qquad \mathrm{(B) \ } 24\sqrt{2}\qquad \mathrm{(C) \ } 36\qquad \mathrm{(D) \ } 24\sqrt{3}\qquad \mathrm{(E) \ } 32\sqrt{2} </math> | |
[[2006 AMC 10B Problems/Problem 24|Solution]] | [[2006 AMC 10B Problems/Problem 24|Solution]] | ||
| Line 188: | Line 188: | ||
Mr. Jones has eight children of different ages. On a family trip his oldest child, who is 9, spots a license plate with a 4-digit number in which each of two digits appears two times. "Look, daddy!" she exclaims. "That number is evenly divisible by the age of each of us kids!" "That's right," replies Mr. Jones, "and the last two digits just happen to be my age." Which of the following is <b><i>not</i></b> the age of one of Mr. Jones's children? | Mr. Jones has eight children of different ages. On a family trip his oldest child, who is 9, spots a license plate with a 4-digit number in which each of two digits appears two times. "Look, daddy!" she exclaims. "That number is evenly divisible by the age of each of us kids!" "That's right," replies Mr. Jones, "and the last two digits just happen to be my age." Which of the following is <b><i>not</i></b> the age of one of Mr. Jones's children? | ||
| − | + | <math> \mathrm{(A) \ } 4\qquad \mathrm{(B) \ } 5\qquad \mathrm{(C) \ } 6\qquad \mathrm{(D) \ } 7\qquad \mathrm{(E) \ } 8 </math> | |
[[2006 AMC 10B Problems/Problem 25|Solution]] | [[2006 AMC 10B Problems/Problem 25|Solution]] | ||
Revision as of 10:26, 1 January 2007
Contents
- 1 Problem 1
- 2 Problem 2
- 3 Problem 3
- 4 Problem 4
- 5 Problem 5
- 6 Problem 6
- 7 Problem 7
- 8 Problem 8
- 9 Problem 9
- 10 Problem 10
- 11 Problem 11
- 12 Problem 12
- 13 Problem 13
- 14 Problem 14
- 15 Problem 15
- 16 Problem 16
- 17 Problem 17
- 18 Problem 18
- 19 Problem 19
- 20 Problem 20
- 21 Problem 21
- 22 Problem 22
- 23 Problem 23
- 24 Problem 24
- 25 Problem 25
- 26 See also
Problem 1
What is ![]() ?
?
![]()
Problem 2
For real numbers ![]() and
and ![]() , define
, define ![]() . What is
. What is ![]() ?
?
![]()
Problem 3
A football game was played between two teams, the Cougars and the Panthers. The two teams scored a total of 34 points, and the Cougars won by a margin of 14 points. How many points did the Panthers score?
![]()
Problem 4
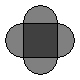
Circles of diameter 1 inch and 3 inches have the same center. The smaller circle is painted red, and the portion outside the smaller circle and inside the larger circle is painted blue. What is the ratio of the blue-painted area to the red-painted area?
![]()
Problem 5
A ![]() rectangle and a
rectangle and a ![]() rectangle are contained within a square without overlapping at any point, and the sides of the square are parallel to the sides of the two given rectangles. What is the smallest possible area of the square?
rectangle are contained within a square without overlapping at any point, and the sides of the square are parallel to the sides of the two given rectangles. What is the smallest possible area of the square?
![]()
Problem 6
A region is bounded by semicircular arcs constructed on the side of a square whose sides measure ![]() , as shown. What is the perimeter of this region?
, as shown. What is the perimeter of this region?
![]()
Problem 7
Which of the folowing is equivalent to ![]() when
when ![]()
![]()
Problem 8
A square of area 40 is inscribed in a semicircle as shown. What is the area of the semicircle?
![]()
Problem 9
Francesca uses 100 grams of lemon juce, 100 grams of sugar, and 400 grams of water to make lemonade. There are 25 calories in 100 grams of lemon juice and 386 calories in 100 grams of sugar. Water contains no calories. How many calories are in 200 grams of her lemonade?
![]()
Problem 10
In a triangle with integer side lengths, one side is three times as long as a second side, and the length of the third side is 15. What is the greatest possible perimeter of the triangle?
![]()
Problem 11
What is the tens digit in the sum ![]()
![]()
Problem 12
The lines ![]() and
and ![]() intersect at the point
intersect at the point ![]() . What is
. What is ![]() ?
?
![]()
Problem 13
Joe and JoAnn each bought 12 ounces of coffee in a 16 ounce cup. Joe drank 2 ounces of his coffee and then added 2 ounces of cream. JoAnn added 2 ounces of cream, stirred the coffee well, and then drank 2 ounces. What is the resulting ratio of the ammount of cream in Joe's coffee to that in JoAnn's coffee?
![]()
Problem 14
Let ![]() and
and ![]() be the roots of the equation
be the roots of the equation ![]() . Suppose that
. Suppose that ![]() and
and ![]() are the roots of the equation
are the roots of the equation ![]() . What is
. What is ![]() ?
?
![]()
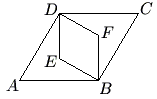
Problem 15
Rhombus ![]() is similar to rhombus
is similar to rhombus ![]() . The area of rhombus
. The area of rhombus ![]() is
is ![]() and
and ![]() . What is the area of rhombus
. What is the area of rhombus ![]() ?
?
![]()
Problem 16
Leap Day, February 29, 2004, occured on a Sunday. On what day of the week will Leap Day, February 29, 2020, occur?
![]()
Problem 17
Bob and Alice each have a bag that contains one ball of each of the colors blue, green, orange, red, and violet. Alice randomly selects one ball from her bag and puts it into Bob's bag. Bob then randomly selects one ball from his bag and puts it into Alice's bag. What is the probability that after this process the contents of the two bags are the same?
![]()
Problem 18
Let ![]() be a sequence for which
be a sequence for which
![]() ,
, ![]() , and
, and ![]() for each positive integer
for each positive integer ![]() .
.
What is ![]() ?
?
![]()
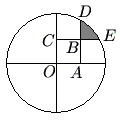
Problem 19
A circle of radius ![]() is centered at
is centered at ![]() . Square
. Square ![]() has side length
has side length ![]() . Sides
. Sides ![]() and
and ![]() are extended past
are extended past ![]() to meet the circle at
to meet the circle at ![]() and
and ![]() , respectively. What is the area of the shaded region in the figure, which is bounded by
, respectively. What is the area of the shaded region in the figure, which is bounded by ![]() ,
, ![]() , and the minor arc connecting
, and the minor arc connecting ![]() and
and ![]() ?
?
![]()
Problem 20
In rectangle ![]() , we have
, we have ![]() ,
, ![]() ,
, ![]() , for some integer
, for some integer ![]() . What is the area of rectangle
. What is the area of rectangle ![]() ?
?
![]()
Problem 21
For a particular peculiar pair of dice, the probabilities of rolling ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , on each die are in the ratio
, on each die are in the ratio ![]() . What is the probability of rolling a total of
. What is the probability of rolling a total of ![]() on the two dice?
on the two dice?
![]()
Problem 22
Elmo makes ![]() sandwiches for a fundraiser. For each sandwich he uses
sandwiches for a fundraiser. For each sandwich he uses ![]() globs of peanut butter at
globs of peanut butter at ![]() ¢ per glob and
¢ per glob and ![]() blobs of jam at
blobs of jam at ![]() ¢ per blob. The cost of the peanut butter and jam to make all the sandwiches is
¢ per blob. The cost of the peanut butter and jam to make all the sandwiches is ![]() . Assume that
. Assume that ![]() ,
, ![]() , and
, and ![]() are positive integers with
are positive integers with ![]() . What is the cost of the jam Elmo uses to make the sandwiches?
. What is the cost of the jam Elmo uses to make the sandwiches?
![]()
Problem 23
A triangle is partitioned into three triangles and a quadrilateral by drawing two lines from vertices to their opposite sides. The areas of the three triangles are 3, 7, and 7 as shown. What is the area of the shaded quadrilateral?
![]()
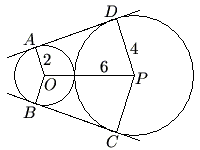
Problem 24
Circles with centers ![]() and
and ![]() have radii
have radii ![]() and
and ![]() , respectively, and are externally tangent. Points
, respectively, and are externally tangent. Points ![]() and
and ![]() on the circle with center
on the circle with center ![]() and points
and points ![]() and
and ![]() on the circle with center
on the circle with center ![]() are such that
are such that ![]() and
and ![]() are common external tangents to the circles. What is the area of the concave hexagon
are common external tangents to the circles. What is the area of the concave hexagon ![]() ?
?
![]()
Problem 25
Mr. Jones has eight children of different ages. On a family trip his oldest child, who is 9, spots a license plate with a 4-digit number in which each of two digits appears two times. "Look, daddy!" she exclaims. "That number is evenly divisible by the age of each of us kids!" "That's right," replies Mr. Jones, "and the last two digits just happen to be my age." Which of the following is not the age of one of Mr. Jones's children?
![]()