Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2016 IMO Problems/Problem 1"

(→‎Problem)
m (→‎Solution 2)
 
(8 intermediate revisions by 2 users not shown)
Line 8: Line 8:
  
 
[[File:2016IMOQ1Solution.jpg|600px]]
 
[[File:2016IMOQ1Solution.jpg|600px]]
 +
 +
The Problem shows that \(\angle DAC = \angle DCA = \angle CAD\), it follows that \(AB \parallel CD\). Extend \(DC\) to intersect \(AB\) at \(G\), we get \(\angle GFA = \angle GFB = \angle CFD\). Making triangles \(\triangle CDF\) and \(\triangle AGF\) similar. Also, \(\angle FDC = \angle FGA = 90^\circ\) and \(\angle FBC = 90^\circ\), which points \(D\), \(C\), \(B\), and \(F\) are concyclic.
 +
 +
And \(\angle BFC = \angle FBA + \angle FAB = \angle FAE = \angle AFE\). Triangle \(\triangle AFE\) is congruent to \(\triangle FBM\), and \(AE = EF = FM = MB\). Let \(MX = EA = MF\), then points \(B\), \(C\), \(D\), \(F\), and \(X\) are concyclic.
 +
 +
Finally \(AD = DB\) and \(\angle DAF = \angle DBF = \angle FXD\).  \(\angle MFX = \angle FXD = \angle FXM\) and \(FE \parallel MD\) with \(EF = FM = MD = DE\), making \(EFMD\) a rhombus. And \(\angle FBD = \angle MBD = \angle MXF = \angle DXF\) and triangle \(\triangle BEM\) is congruent to \(\triangle XEM\), while \(\triangle MFX\) is congruent to \(\triangle MBD\) which is congruent to \(\triangle FEM\), so \(EM = FX = BD\).
 +
 +
~Athmyx
 +
 +
== Solution 2 ==
 +
Let <math>\angle FBA = \angle FAB = \angle FAD = \angle FCD = \alpha</math>. And WLOG, <math>MF = 1</math>. Hence, <math>CF = 2</math>,
 +
 +
<math>\implies</math> <math>BF = CF.cos(2\alpha) = 2.cos(2\alpha) = FA</math>,
 +
 +
<math>\implies</math> <math>DA = \frac{AC}{2cos(\alpha)} = \frac{CF+FA}{2cos(\alpha)} = \frac{2+2cos(2\alpha)}{2cos(\alpha)} = \frac{1+cos(2\alpha)}{cos(\alpha)}</math> and
 +
 +
<math>\implies</math> <math>DE = AE = \frac{DA}{2cos(\alpha)} = \frac{1+cos(2\alpha)}{2.(cos(\alpha))^2} = 1</math>.
 +
 +
So <math>MX = DE = 1</math> which means <math>B</math>, <math>C</math>, <math>X</math> and <math>F</math> are concyclic. We know that <math>DE || MC</math> and <math>DE = 1 = MC</math>, so we conclude <math>MCDE</math> is parallelogram. So <math>\angle AME = \alpha</math>. That means <math>MDEA</math> is isosceles trapezoid. Hence, <math>MD = EA = 1</math>. By basic angle chasing,
 +
 +
<math>\angle MBF = \angle MFB = 2\alpha</math> and <math>\angle MXD = \angle MDX = 2\alpha</math> and we have seen that <math>MB = MF = MD = MX</math>, so <math>BFDX</math> is isosceles trapezoid. And we know that <math>ME</math> bisects <math>\angle FMD</math>, so <math>ME</math> is the symmetrical axis of <math>BFDX</math>.
 +
 +
<math>B</math> and <math>X</math>, <math>D</math> and <math>E</math> are symmetrical respect to <math>ME</math>. Hence, the symmetry of <math>BD</math> with respect to <math>ME</math> is <math>FX</math>. And we are done <math>\blacksquare</math>.
 +
 +
~EgeSaribas
  
 
==See Also==
 
==See Also==
  
 
{{IMO box|year=2016|before=First Problem|num-a=2}}
 
{{IMO box|year=2016|before=First Problem|num-a=2}}

Latest revision as of 12:16, 19 May 2024

Problem

Triangle $BCF$ has a right angle at $B$. Let $A$ be the point on line $CF$ such that $FA=FB$ and $F$ lies between $A$ and $C$. Point $D$ is chosen so that $DA=DC$ and $AC$ is the bisector of $\angle{DAB}$. Point $E$ is chosen so that $EA=ED$ and $AD$ is the bisector of $\angle{EAC}$. Let $M$ be the midpoint of $CF$. Let $X$ be the point such that $AMXE$ is a parallelogram. Prove that $BD,FX$ and $ME$ are concurrent.

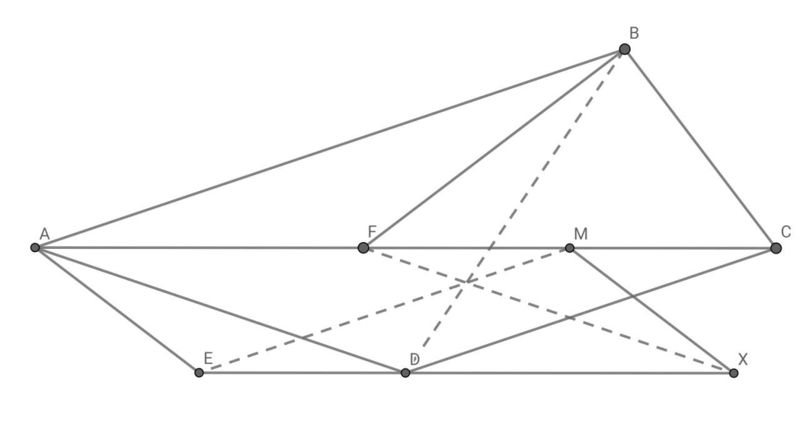
2016IMOQ1.jpg

Solution

2016IMOQ1Solution.jpg

The Problem shows that \(\angle DAC = \angle DCA = \angle CAD\), it follows that \(AB \parallel CD\). Extend \(DC\) to intersect \(AB\) at \(G\), we get \(\angle GFA = \angle GFB = \angle CFD\). Making triangles \(\triangle CDF\) and \(\triangle AGF\) similar. Also, \(\angle FDC = \angle FGA = 90^\circ\) and \(\angle FBC = 90^\circ\), which points \(D\), \(C\), \(B\), and \(F\) are concyclic.

And \(\angle BFC = \angle FBA + \angle FAB = \angle FAE = \angle AFE\). Triangle \(\triangle AFE\) is congruent to \(\triangle FBM\), and \(AE = EF = FM = MB\). Let \(MX = EA = MF\), then points \(B\), \(C\), \(D\), \(F\), and \(X\) are concyclic.

Finally \(AD = DB\) and \(\angle DAF = \angle DBF = \angle FXD\). \(\angle MFX = \angle FXD = \angle FXM\) and \(FE \parallel MD\) with \(EF = FM = MD = DE\), making \(EFMD\) a rhombus. And \(\angle FBD = \angle MBD = \angle MXF = \angle DXF\) and triangle \(\triangle BEM\) is congruent to \(\triangle XEM\), while \(\triangle MFX\) is congruent to \(\triangle MBD\) which is congruent to \(\triangle FEM\), so \(EM = FX = BD\).

~Athmyx

Solution 2

Let $\angle FBA = \angle FAB = \angle FAD = \angle FCD = \alpha$. And WLOG, $MF = 1$. Hence, $CF = 2$,

$\implies$ $BF = CF.cos(2\alpha) = 2.cos(2\alpha) = FA$,

$\implies$ $DA = \frac{AC}{2cos(\alpha)} = \frac{CF+FA}{2cos(\alpha)} = \frac{2+2cos(2\alpha)}{2cos(\alpha)} = \frac{1+cos(2\alpha)}{cos(\alpha)}$ and

$\implies$ $DE = AE = \frac{DA}{2cos(\alpha)} = \frac{1+cos(2\alpha)}{2.(cos(\alpha))^2} = 1$.

So $MX = DE = 1$ which means $B$, $C$, $X$ and $F$ are concyclic. We know that $DE || MC$ and $DE = 1 = MC$, so we conclude $MCDE$ is parallelogram. So $\angle AME = \alpha$. That means $MDEA$ is isosceles trapezoid. Hence, $MD = EA = 1$. By basic angle chasing,

$\angle MBF = \angle MFB = 2\alpha$ and $\angle MXD = \angle MDX = 2\alpha$ and we have seen that $MB = MF = MD = MX$, so $BFDX$ is isosceles trapezoid. And we know that $ME$ bisects $\angle FMD$, so $ME$ is the symmetrical axis of $BFDX$.

$B$ and $X$, $D$ and $E$ are symmetrical respect to $ME$. Hence, the symmetry of $BD$ with respect to $ME$ is $FX$. And we are done $\blacksquare$.

~EgeSaribas

See Also

2016 IMO (Problems) • Resources
Preceded by
First Problem 		1 • 2 • 3 • 4 • 5 • 6 Followed by
Problem 2
All IMO Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2016_IMO_Problems/Problem_1&oldid=219514"