Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Spieker center"

(→‎Intersection of three cleavers)
(→‎Intersection of three cleavers)
Line 35: Line 35:
  
 
Therefore, the three cleavers meet at the Spieker center.
 
Therefore, the three cleavers meet at the Spieker center.
 +
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
==Radical center of excircles==
 +
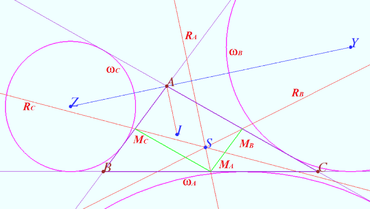
[[File:Radical center.png|370px|right]]
 +
Prove that the Spieker center of triangle is the radical center of the three excircles.
 +
 +
<i><b>Proof</b></i>
 +
 +
Let <math>\triangle ABC</math> be given,<math>M_A, M_B, M_C</math> be the midpoints of <math>BC, AC, BC,</math> respectively.
 +
 +
Let <math>\omega_A, \omega_B, \omega_C</math> be A-excircle, B-excircle, C-excircle centered at <math>X,Y,Z,</math> respectively.
 +
 +
Let <math>I</math> be the incenter of <math>\triangle ABC.</math>
 +
Let <math>R_A</math> be the radical axis of <math>\omega_B</math> and <math>\omega_C, R_B</math> be the radical axis of <math>\omega_A</math> and <math>\omega_C, R_C</math> be the radical axis of <math>\omega_B</math> and <math>\omega_A,</math> respectively.
 +
 +
It is known that the distances from <math>B</math> to the tangent points of <math>\omega_C</math> is equal to the distances from <math>C</math> to the tangent points of <math>\omega_B, BM_A = CM_A</math> therefore <math>M_A</math> lies on the radical axis <math>R_A</math> of <math>\omega_B</math> and <math>\omega_C.</math> Similarly, <math>M_B \in R_B, M_C \in R_C.</math>
 +
 +
<math>AI \perp ZY, R_A \perp XY \implies AI || RA \implies R_A</math> is cleaver, so the radical center of the three excircles coinside with the intersection of the three cleavers of triangle.
  
 
'''vladimir.shelomovskii@gmail.com, vvsss'''
 
'''vladimir.shelomovskii@gmail.com, vvsss'''

Revision as of 15:42, 7 August 2023

The Spieker center is defined as the center of mass of the perimeter of the triangle. The Spieker center of a $\triangle ABC$ is the center of gravity of a homogeneous wire frame in the shape of $\triangle ABC.$ The Spieker center is a triangle center and it is listed as the point $X_{10}.$

Incenter of medial triangle

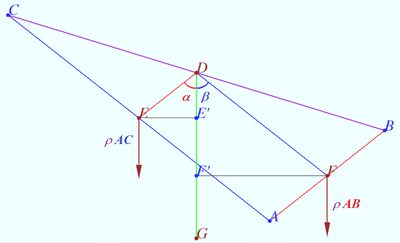
Physical proof.png

Prove that the Spieker center of triangle $\triangle ABC$ is the incenter of the medial triangle $\triangle DEF$ of a $\triangle ABC.$

Proof

Let's hang up the $\triangle ABC$ in the middle of side $BC.$ Side $BC$ is balanced.

Let's replace side $AC$ with point $E$ (the center of mass of $AC,$ the midpoint $AC).$ Denote $\rho$ the linear density of a homogeneous wire frame.

The mass of point $E$ is equal to $\rho \cdot AC,$ the shoulder of the gravity force is $EE' = ED \sin \alpha = \frac {AB \sin \alpha }{2}.$

The moment of this force is $g EE' \rho \cdot AC = \frac {g \rho\cdot AC \cdot AB}{2} \sin \alpha.$

Similarly the moment gravity force acting on AB is $\frac {g \rho\cdot AC \cdot AB}{2} \sin \beta.$

Therefore, equilibrium condition is $\alpha = \beta$ and the center of gravity of a homogeneous wire frame $ABC$ lies on each bisector of $\triangle DEF.$

This point is the incenter of the medial triangle $\triangle DEF.$

vladimir.shelomovskii@gmail.com, vvsss

Intersection of three cleavers

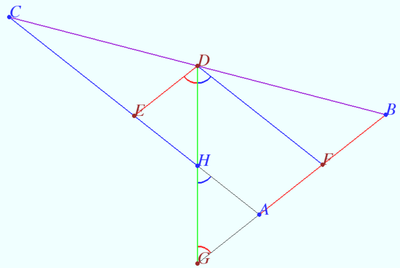
Cleaver.png

Prove that the Spieker center is located at the intersection of the three cleavers of triangle. A cleaver of a triangle is a line segment that bisects the perimeter of the triangle and has one endpoint at the midpoint of one of the three sides.

Proof

We use notation of previous proof. $DG$ is the segment contains the Spieker center, $G \in AB, \angle EDG = \angle FDG, H = DG \cap AC.$ WLOG, $AC > AB.$ \[DF||AC \implies \angle AHG = \angle FDG.\] Similarly, $\angle AGH = \angle EDG = \angle AHG.$

So $AH = AG \implies CH = AB + AH \implies DH$ is cleaver.

Therefore, the three cleavers meet at the Spieker center.

vladimir.shelomovskii@gmail.com, vvsss

Radical center of excircles

Radical center.png

Prove that the Spieker center of triangle is the radical center of the three excircles.

Proof

Let $\triangle ABC$ be given,$M_A, M_B, M_C$ be the midpoints of $BC, AC, BC,$ respectively.

Let $\omega_A, \omega_B, \omega_C$ be A-excircle, B-excircle, C-excircle centered at $X,Y,Z,$ respectively.

Let $I$ be the incenter of $\triangle ABC.$ Let $R_A$ be the radical axis of $\omega_B$ and $\omega_C, R_B$ be the radical axis of $\omega_A$ and $\omega_C, R_C$ be the radical axis of $\omega_B$ and $\omega_A,$ respectively.

It is known that the distances from $B$ to the tangent points of $\omega_C$ is equal to the distances from $C$ to the tangent points of $\omega_B, BM_A = CM_A$ therefore $M_A$ lies on the radical axis $R_A$ of $\omega_B$ and $\omega_C.$ Similarly, $M_B \in R_B, M_C \in R_C.$

$AI \perp ZY, R_A \perp XY \implies AI || RA \implies R_A$ is cleaver, so the radical center of the three excircles coinside with the intersection of the three cleavers of triangle.

vladimir.shelomovskii@gmail.com, vvsss

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Spieker_center&oldid=196571"