2006 AMC 10/12 B Math Jam
Go back to the Math Jam ArchiveAoPS Instructors will lead a discussion of the harder problems and requested problems from both the 2006 AMC 10 B and the 2006 AMC 12 B.
Copyright © 2025 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.
Facilitator: Dave Patrick
DPatrick (19:01:43)
Hello and welcome to the 2006 AMC 10B/12B Math Jam!
DPatrick (19:01:51)
Before we get started I would like to take a moment to explain our virtual classroom to those who have not previously participated in a Math Jam or one of our online classes.
DPatrick (19:02:01)
The classroom is moderated meaning that students can type into the classroom, but only the moderators can choose a comment to drop into the classroom. This helps keep the class organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read. Also, only moderators can enter into private chats with other people in the classroom.
DPatrick (19:02:17)
Additionally, the virtual classroom is LaTeX enabled. LaTeX allows users to make nice equations and other math expressions. If you would like to learn how to write in LaTeX, click on the tab on the left side panel of our website and there is a tutorial and reference guide there.
DPatrick (19:02:29)
Using LaTeX in the virtual classroom is slightly different than using it on the message board or in a LaTeX editor. If anything you type up in a post that uses LaTeX then you must use a semicolon (;) to begin your post. For example, if you type
DPatrick (19:02:35)
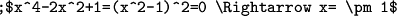
DPatrick (19:02:41)
This message will look like this when posted in the classroom:
DPatrick (19:02:50)
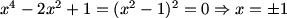
DPatrick (19:03:01)
Just remember, if your post uses LaTeX, use the semicolon (;) to begin your post!
DPatrick (19:03:12)
Lastly, some of the problems and diagrams in today's discussion are a bit large. I will generally post a link to the problems and diagrams, so that you can open them in a separate window. You should be able to just click on the link. You might have to hold down the Ctrl key while clicking. If this doesn't work, you may need to disable your popup blocker.
DPatrick (19:03:26)
You can also widen the chat window by dragging the vertical bar which separates the chat from the list of usernames.
DPatrick (19:03:40)
For those of you new to our AMC Math Jams, what we'll be doing today is working through detailed solutions of Problems 21-25 on the AMC 10B and 12B. A nice feature this year is that all but one of problems 21-25 on the 10B were also problems on the 12B.
DPatrick (19:04:02)
Let's start with #21 of the 10B, which is also #17 on the 12B.
DPatrick (19:04:05)

DPatrick (19:04:09)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-168846628.gif
DPatrick (19:04:38)
(As I mentioned above, you can click the link to popup the problem in a separate window, which is handy for following along as we work though the solution.)
DPatrick (19:04:55)
How can we begin on this problem?
Kakashi (19:04:47)
you can roll (1,6) (2,5) (3,4) (4,3) (5,2) (6,1)
eryaman (19:04:56)
find the probability of each number, then combos 1/6, 2/5, 3/4, 6/1, 5/2, 4/3
DPatrick (19:05:19)
Right, first we can observe that there are six ways it can happen: 1-6, 2-5, 3-4, 4-3, 5-2, and 6-1.
DPatrick (19:05:39)
So we can find the probability for each pair, then sum them up.
mna851 (19:05:09)
Set the probability of rolling a 1 euqal to p
DPatrick (19:06:07)
OK, let p denote the probability of rolling a 1 on one die.
DPatrick (19:06:12)
Then what are the probabilities of the other numbers on the die?
The Zuton Force (19:06:35)
2p 3p 4p 5p 6p
eryaman (19:06:39)
2p, 3p, 4p, 5p, 6p
mna851 (19:06:39)
2p, 3p, 4p, 5p, 6p
DPatrick (19:06:50)
Right: the probability of rolling a 2 is 2p, of rolling a 3 is 3p, and so on.
Bictor717 (19:06:06)
The sum of the probabilities is 1
DPatrick (19:07:06)
Exactly -- the sum of the probabilities of the 6 sides must sum to 1.
DPatrick (19:07:14)
Therefore, we can solve for p.
Thorn (19:07:13)
So we have p + 2p + 3p + 4p + 5p + 6p = 1
perfectnumber628 (19:07:10)
p=1/21
DPatrick (19:07:31)
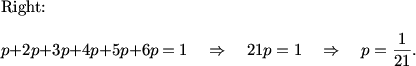
DPatrick (19:07:44)
So the probability of rolling a 1 is 1/21, of rolling a 2 is 2/21, and so on.
Thorn (19:07:48)
The rest is just arithmetic.
DPatrick (19:08:08)
Yep -- now we can sum up the six different ways of rolling a 7.
eryaman (19:08:12)
so 2((1/21)(6/21)+(2/21)(5/21)+(3/21)(4/21))
DPatrick (19:08:49)
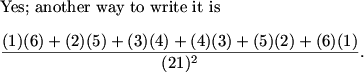
DPatrick (19:09:17)
This simplifies to 56/(21)^2 = 8/63. So the answer is (C).
DPatrick (19:10:09)
Next is #22 on the 10B, which is also #14 on the 12B.
DPatrick (19:10:17)

DPatrick (19:10:21)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-105292725.gif
DPatrick (19:10:45)
We need to translate the words into a mathematical formula that we can deal with. What's the formula?
jli (19:10:29)
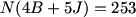
The Zuton Force (19:11:07)
N(4B+5J)=253
perfectnumber628 (19:11:11)
N(4B+5J)=253
DPatrick (19:11:24)
Each sandwich costs 4B + 5J cents to make, and there are N sandwiches which altogether cost 253 cents.
DPatrick (19:11:36)
So N(4B+5J) = 253.
DPatrick (19:11:40)
Now what?
demonface (19:11:18)
the factors of 253 is 11 and 23
jiangwei (19:11:43)
253=11*23
mna851 (19:11:43)
253=23*11
jli (19:11:43)
253=11*23
Kakashi (19:11:47)
N, B, J are all integers
DPatrick (19:12:06)
Yes, since everything in sight is a positive integer, both N and 4B+5J must be factors of 253.
perfectnumber628 (19:11:38)
n is 1, 11, 23, or 253
DPatrick (19:12:37)
Could N be either 1 or 253?
The Zuton Force (19:12:35)
n > 1
eryaman (19:12:42)
perfectnumber: the problem gives you that N>1
DPatrick (19:13:02)
Right, so we can rule that out.
DPatrick (19:13:05)
Could N be 253?
perfectnumber628 (19:13:02)
no, n>1 and 4B+5J will be greater than 1
DPatrick (19:13:40)
4B+5J cannot be 1 either (since B and J are positive), so N and 4B+5J must be 11 and 23 (in either order).
mel (19:12:40)
We know that multiples of 4 and 5 cannot sum to 1 or 11. So we try to get it to sum to 23.
demonface (19:12:46)
so we find out whether adding 4 and 5s can make 23 or 11
The Zuton Force (19:14:01)
you need at least one J and one B... once you're already at 9, you can't get to 11
DPatrick (19:14:14)
Yes, a little trial-and-error tells us that 4B+5J cannot equal 11 if B and J are positive integers, so we must have 4B + 5J = 23 and N = 11.
jiangwei (19:12:51)
B=2, J=3
eryaman (19:14:22)
4(2)+5(3)=23
perfectnumber628 (19:14:25)
B=2 and J=3
DPatrick (19:14:45)
Guess-and-check then gives B=2 and J=3.
DPatrick (19:14:50)
So how do we finish?
The Zuton Force (19:14:53)
15*11 = 165 -> $1.65
mna851 (19:14:56)
So each jelly sandwich costs 15 cents and since there a 11 of them the total cost is 15*11
DPatrick (19:15:14)
Yes: the cost of jam used is N(5J) = 11(15) = 165 cents, or $1.65. Answer (D).
DPatrick (19:15:49)
This is a simple example of a [b]Diophantine equation[/b]: an equation in which we're looking for integer solutions.
DPatrick (19:16:02)
Often, as in this case, prime factors are the key.
DPatrick (19:16:09)
#23 on the 10B is next (this problem did not appear on the 12B).
DPatrick (19:16:17)

DPatrick (19:16:28)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-198888500.gif
DPatrick (19:16:41)

DPatrick (19:16:51)
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/dda940a97180e4ee2e702f8a762dc922.png
DPatrick (19:17:07)
Any ideas?
mna851 (19:17:28)
Use the ratio of the bases and heights
jli (19:17:32)
draw the other line froom the vertex through the middle point
DPatrick (19:17:43)
These are two good ideas.
DPatrick (19:17:57)
We probably want to exploit the ""same base"" or ""same height"" principle, which states that the ratio of areas of two triangles with the same base (or same height) is proportional to the ratio of their heights (or bases).
DPatrick (19:18:16)
But that quadrilateral is ugly to work with.
DPatrick (19:18:28)
We can split it up into two triangles (I'm also going to label the points and the two new triangles for our convenience):
DPatrick (19:18:38)
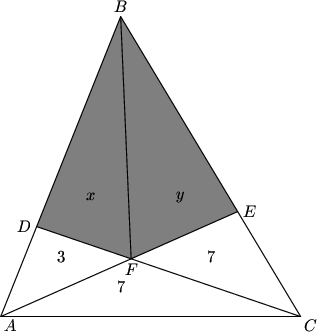
DPatrick (19:18:40)
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/0a9a6fbe5583dae83c2a8b2def5bcc19.png
DPatrick (19:18:51)
What are some ratios of areas that we can now state?
DPatrick (19:20:05)
For example, triangles FDA and FDB share a height from F down to base AB.
DPatrick (19:20:37)
So the areas of FDA and FDB have the same ratio as the bases AD and AB.
DPatrick (19:21:10)
Is there another pair of triangles that have the same height and also have bases AD and AB?
eryaman (19:21:11)
AD/DB=3/x
DPatrick (19:21:30)
Right -- that's from our first pair of triangles.
DPatrick (19:21:41)
Is there another pair with ratio AD/DB?
Ars (19:22:07)
ADC and CDB
topaz (19:22:15)
ADC and BDC
DPatrick (19:22:44)
Good, both triangle ADC and BDC have the same height from C down to base AB.
DPatrick (19:23:03)
So the ratio of the areas of ADC and BDC equals the ratio of the bases AD and DB.
jli (19:22:19)
10/(x+y+7)
DPatrick (19:23:28)
Right, we get AD/DB = 10/(x+y+7) using triangles ADC and BDC.
DPatrick (19:23:35)
This gives us our first equation:
DPatrick (19:23:48)
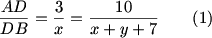
DPatrick (19:24:23)
Now let's try using this ""same height"" principle on triangles with bases CE and EB. What triangles can we use?
eryaman (19:24:37)
FBE and FEC
perfectnumber628 (19:24:41)
CFE and EFB
DPatrick (19:25:04)
Good, FEB and FEC share a height from F to base BC.
DPatrick (19:25:16)
So what is BE/EC equal to for these triangles?
shinwoo (19:25:36)
y/7
eryaman (19:25:39)
y/7
DPatrick (19:25:52)
Yep: BE/EC is the ratio of the areas, which is y/7.
DPatrick (19:26:07)
Is there another pair of triangles sharing a height to bases BE and EC?
perfectnumber628 (19:26:17)
AEC and AEB
topaz (19:26:20)
ABE and AEC
DPatrick (19:26:37)
Yes: AEB and AEC share a height from F down to BE and EC.
DPatrick (19:26:47)
What's the ratio of BE/EC for these triangles?
eryaman (19:27:14)
(3+x+y)/14
DPatrick (19:27:41)
Yes, it's the ratio of the areas of AEB and AEC, which is (3+x+y)/14.
DPatrick (19:27:47)
This gives us our second equation:
DPatrick (19:27:52)
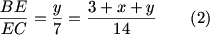
DPatrick (19:28:03)
What next?
eryaman (19:28:15)
so we have two equations, two variables, then i guess we could solve for the varialbes
jli (19:28:15)
system of 2 equations
DPatrick (19:28:47)
Yes, we can take equations (1) and (2) and set up a system of two equations in two variables.
DPatrick (19:28:58)
I would get rid of the denominators before doing anything else.
DPatrick (19:29:22)
...and move the x and y terms to one side of each equation, and the constant to the other.
DPatrick (19:29:35)
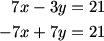
me@home (19:29:50)
now add the equations
DPatrick (19:30:16)
Yes, when written this way, solving is a breeze. We can add them to get 4y = 42.
eryaman (19:29:51)
so y=10.5
jli (19:30:04)
y=10.5
me@home (19:30:16)
4y=42, y=10.5
DPatrick (19:30:35)
So what's x, and what's the final answer?
perfectnumber628 (19:30:38)
x=7.5
DPatrick (19:30:59)
Plugging back in gives 7x=21+63/2=105/2, so x=15/2.
jli (19:31:00)
18
DPatrick (19:31:15)
So x+y = 18. Answer (D).
DPatrick (19:32:00)
The key step was using the ""same base/same height"" principle: that if two triangles share a base (or a height), then we can write a ratio of their areas in terms of a ratio whichever one (base or height) that they don't share.
DPatrick (19:32:13)
This is pretty common in problems involving areas of triangles but not much else (like this one).
DPatrick (19:32:29)
Next is #24 on the 10B, which is #15 on the 12B.
DPatrick (19:32:34)

DPatrick (19:32:38)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-131275396.gif
DPatrick (19:32:46)

DPatrick (19:32:51)
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/7ef2a58a812bf43f5c031b799c4a7626.png
DPatrick (19:33:07)
How shall we proceed?
demonface (19:33:03)
lets draw a rectangle
4everwise (19:33:15)
draw segment from O parallel to AD to meet DP
demonface (19:33:17)
from o to the middle of dp and cp
DPatrick (19:33:40)
We almost certainly need to drop perpendiculars from O to PD and PC. Let's label the new points X and Y.
DPatrick (19:33:49)

DPatrick (19:33:52)
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/a3f6d9d84e7aa8f74f3ab930fe9cbf50.png
DPatrick (19:34:00)
This pretty much finishes the problem!
The Zuton Force (19:33:28)
then use the pythagorean theorem
4everwise (19:34:02)
Now we can use pythagoras to find OX
demonface (19:34:08)
6^2-2^2=32 so its 4rt2
DPatrick (19:34:35)
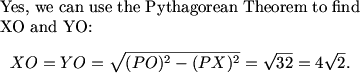
DPatrick (19:34:56)
(We note that ADXO is a rectangle (and so is OYCB), so DX = AO = 2 and PX = PD-DX = 2.)
DPatrick (19:35:14)
So now we can just add up the areas.
eryaman (19:35:13)
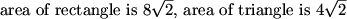
DPatrick (19:35:48)
Yes:
[ADXO] = [BOYC] = (AO)(OX) = 8*sqrt(2).
[OPX] = [OPY] = 1/2(PX)(OX) = 4*sqrt(2).
shinwoo (19:35:40)
the answer's B
og4life_42592 (19:35:53)
[b]answer's B[/b]
DPatrick (19:36:12)
So the area of the hexagon is 8sqrt(2)+4sqrt(2)+4sqrt(2)+8sqrt(2) = 24*sqrt(2), answer (B).
DPatrick (19:36:59)
Last on the 10B is #25, which is also #19 on the 12B.
DPatrick (19:37:04)

DPatrick (19:37:09)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-193805656.gif
DPatrick (19:37:44)
There's a lot of information to parse in this problem. When presented with a problem statement this complicated, I highly recommend reading it twice.
DPatrick (19:38:07)
For ease of referring to it, let's call the 4-digit number N.
DPatrick (19:38:30)
Are there any answers that we can eliminate right away?
demonface (19:37:31)
we know that since 9 and 2 are there, 6 is there too along with 4
dimak11214 (19:38:41)
6
Ars (19:38:45)
4 and 6
danthemanvt (19:38:48)
it must be divisible by 2 and 3 since they aren't in the list, so its divisib;e by6
mna851 (19:38:53)
4
DPatrick (19:39:20)
Yes, we know N is divisible by 2 and 3, so it must be divisible by 6.
DPatrick (19:39:37)
The answer also can't be 4, since if N is not divisible by 4, then it's also not divisible by 8.
DPatrick (19:39:51)
So the ""bad"" number (the only that N is not divisible by) must be 5, 7, or 8.
DPatrick (19:40:09)
Now what?
og4life_42592 (19:40:25)
plug in number's
pilot (19:40:32)
guess and check
DPatrick (19:40:46)
Meaning what exactly?
DPatrick (19:41:02)
Which number should we test first?
dimak11214 (19:40:50)
Would it help that the digits add up to 9.
DPatrick (19:41:32)
Definitely -- since N is divisible by 9, the two digits have to sum to 9. This narrows our possibilities for N considerably.
perfectnumber628 (19:41:23)
i tested 5
DPatrick (19:42:00)
5 is probably the best one to test, since the divisibilty by 5 condition is so strong.
DPatrick (19:42:10)
N is divisible by 5 if and only if the last digit is 5 or 0.
Kakashi (19:42:19)
cant be 5 cus its even
DPatrick (19:42:45)
Right, the last digit can't be 5, since we know that 2 divides N.
DPatrick (19:43:08)
So that leaves 9900 or 9090 as the only possibilities.
pilot (19:43:12)
so it must be 9900 or 9090 but neither of those work
DPatrick (19:43:29)
Specificially, why don't they work?
mna851 (19:43:30)
but 9900 can't be b/c the last digits wouldnt be the fatheres age
DPatrick (19:44:11)
Right -- we know that the last two digits are the father's age, and his age of ""00"" is absurd.
Impossible (19:44:08)
9090 isnt divisible by 4
DPatrick (19:44:36)
And 9090 can't work since it's not a multiple of 4 (which we know N has to be).
dimak11214 (19:44:35)
so 5 is out
DPatrick (19:45:01)
Yes, that's it: N cannot be divisible by 5, and hence (B) is the answer.
jiangwei (19:44:50)
5544
perfectnumber628 (19:45:15)
N could be 5544
DPatrick (19:45:38)
Right. We know that N is divisible by 7, 8, and 9, so N must be a multiple of 7*8*9 = 504.
DPatrick (19:45:44)
Then we can easily see that N = 11*504 = 5544 is the license plate.
DPatrick (19:46:11)
There are lots of ways to do this problem -- the way that we just worked through it is essentially the way that I first did it.
DPatrick (19:46:38)
You could have tried to find N directly (as I just did above) and gotten it that way too.
DPatrick (19:46:55)
Now we'll move on to the last 5 AMC 12B problems.
DPatrick (19:47:02)
We'll start with #21.
DPatrick (19:47:08)

DPatrick (19:47:16)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-19823188.gif
DPatrick (19:48:00)
The first thing I would do with this problem is sketch a picture.
DPatrick (19:48:07)

DPatrick (19:48:10)
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/5debecb8103f18cf264e5853c881f51a.png
eryaman (19:47:47)
if x and y are the sides, then xy=2006
DPatrick (19:48:33)
OK, let the two sides of the rectangle have lengths x and y.
DPatrick (19:48:43)
Then we're given that xy = 2006. We want to find 2(x+y).
Thorn (19:49:07)
Now, since B and D are foci, I would connect BD to draw the major axis of the ellopse.
eryaman (19:49:18)
we can draw and try to find the lengtsh of the major/minor axis
DPatrick (19:49:40)
Before we do that, to solve this problem, we need to know how an ellipse is described in terms of its foci.
DPatrick (19:49:48)
What exactly is an ellipse?
The Zuton Force (19:50:09)
distances from foci to a point on the elipse sum to a constant
eryaman (19:50:22)
the set of all points such that the sum of the distances from the foci is a certain number
DPatrick (19:50:34)
Exactly.
me@home (19:50:21)
the locus of points that a pencil attached to a string with enpoints at B,D
DPatrick (19:50:54)
Yes, this is a practical way to draw one (the length of the string is the sum of the distances to the two foci).
DPatrick (19:51:17)
So for any point P on the ellipse, the sum PB + PD is constant.
perfectnumber628 (19:51:07)
so x+y is the distance from the foci to any point on the ellipse
DPatrick (19:51:52)
Right! We could take the point A, and we get that this constant distance is PB + PD = x+y.
DPatrick (19:52:07)
So how can we use that to find the lengths of the axes of the ellipse?
DPatrick (19:52:28)
Let's do the easier axis first, which is the major axis (the axis that includes the two foci).
DPatrick (19:52:48)
What's its length?
perfectnumber628 (19:52:38)
the string length (x+y) equals the length of the major axis
Bictor717 (19:52:51)
2a=x+y
DPatrick (19:53:14)
Right. This is another basic fact about ellipses.
DPatrick (19:53:20)
The length of the major axis (the one including the foci) is just the common distance sum, so 2a = x+y.
DPatrick (19:53:31)
How do we find the other (minor) axis?
eryaman (19:52:15)
so if we draw lines from the foci to the ""top"" of the ellipse, then each line will have (x+y)/2
DPatrick (19:54:10)

DPatrick (19:54:14)
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/2662cb2341f3beb42e7bcd86006f2237.png
DPatrick (19:54:31)
Right.
DPatrick (19:54:44)
""d"" in this picture is the distance between the foci.
DPatrick (19:54:49)
But what is d?
alan (19:54:52)
d=√x2+y2
alan (19:55:03)
diagonal of the rectangle
perfectnumber628 (19:55:03)
d is the diagonal of the rectangle
duckpaladin88 (19:55:08)
d = square root of x^2 + y^2
DPatrick (19:55:21)
Exactly -- d is the diagonal of the rectangle.
eryaman (19:55:11)
pythag theorem...
DPatrick (19:55:45)
Right, we can use the Pythagorean Theorem to find b.
DPatrick (19:55:54)
(actually we can multiply by 2 to get rid of the fractions and find 2b instead):
DPatrick (19:56:04)
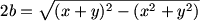
DPatrick (19:56:17)
How does this simplify?
anniesez (19:56:16)
so 2xy is left
eryaman (19:56:24)
so 2b = sqrt(2xy)
Teki-Teki (19:56:28)
2b = sqrt( 2xy )
me@home (19:56:28)
sqrt(2xy) = 2b
Ars (19:56:32)
2b=sqrt(2xy)
4everwise (19:56:37)
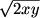
The Zuton Force (19:56:37)
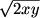
DPatrick (19:56:54)
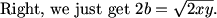
anniesez (19:56:23)
but that's 2006
Bictor717 (19:57:05)
xy=2006
DPatrick (19:57:20)
Yes! xy = 2006 is the area of the rectangle.
DPatrick (19:57:40)
So we can solve for b!
me@home (19:57:56)
sqrt(1003)
Impossible (19:58:00)
b=(1003)^(1/2)
anniesez (19:58:02)
b= sqrt 1003?
DPatrick (19:58:09)
Yes, b = sqrt(1003).
DPatrick (19:58:19)
We're very close now!
DPatrick (19:58:30)
What's a?
Bictor717 (19:58:29)
ab=2006
DPatrick (19:58:59)
Yes, the problem told us that the area of the ellipse was 2006pi, and it also (nicely!) told use that this area is pi*ab.
duckpaladin88 (19:59:32)
so a = 2*sqrt*1003
JHu (19:59:45)
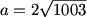
DPatrick (20:00:02)
Right, we can solve for a and get a = 2*sqrt(1003).
me@home (19:59:37)
a is half the perimeter!!
DPatrick (20:00:13)
Almost...
Bictor717 (20:00:13)
2a=x+y
DPatrick (20:00:29)
Right, so a is 1/4 of the perimeter.
4everwise (20:00:13)
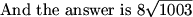
alan (20:00:34)
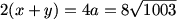
DPatrick (20:00:42)
And we're done! Choice (C).
DPatrick (20:01:27)
You had to know what it meant for something to be an ellipse to make any headway in this problem, but if you did know what an ellipse was, and drew the right picture, the problem was manageable.
DPatrick (20:01:51)
Now on to #22:
DPatrick (20:01:53)
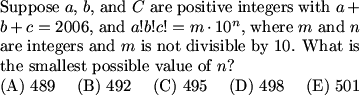
DPatrick (20:01:59)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-175196001.gif
DPatrick (20:02:18)
What are we [i]really[/i] trying to find here?
eryaman (20:02:32)
number of 5's
alan (20:02:38)
number of 5's
mna851 (20:02:38)
Three numbers whose factorials have the least factors of 5 in them
Thorn (20:02:43)
We are trying to count how many factors of 5 are in a!b!c!
DPatrick (20:02:58)
Right, since in factorials, powers of 10 are really determined by powers of 5, we're really looking to count the number of powers of 5 in a!b!c!.
DPatrick (20:03:29)
There are really only two reasonable guesses to try at this point for a,b,c.
jiangwei (20:02:29)
624, 624,
The Zuton Force (20:02:50)
We want to minimize the factors of 10, and hence the factors of 5. 625 has many powers of 5 because it is a power of 5, so setting a and b to 624 will cause you to loose several factors of 5 without inflating c.
alan (20:03:38)
624
topaz (20:03:48)
624...
DPatrick (20:04:39)
That's one very reasonable guess: to set a=b=624 and thus 758, for the reason that Zuton describes (since 625 has a lot of powers of 5 and thus should be avoided).
perfectnumber628 (20:04:09)
a, b, and c must be equal or close to each other if a!b!c! is small
DPatrick (20:05:10)
That's the other very reasonable guess: to make them as equal as possible: a=668 and b=c=669.
DPatrick (20:05:26)
Once we have a guess, how do we count the powers of 5?
Thorn (20:03:31)
To count how many factors of 5 are in N, we take N/5 + n/25 + N/125 + N/625
perfectnumber628 (20:05:44)
divide by 5, and 25, and 125
DPatrick (20:05:56)
Right.
Bictor717 (20:05:56)
floor function'd
DPatrick (20:06:08)
Exactly.
DPatrick (20:06:52)
The number of powers of 5 in N! is [N/5] + [N/25] + [N/125] + [N/625], where [x] means the floor function, or the largest integer less than or equal x.
dimak11214 (20:06:33)
668,669 has 495 5's
DPatrick (20:07:33)
Right, if we check our guess a=668 and b=c=669, we get
[668/5] + [668/25] + [668/125] + [668/625]
133 + 26 + 5 + 1 = 165.
DPatrick (20:07:44)
(669 doesn't add a power of 5).
DPatrick (20:07:52)
So that's 3*165 = 495 powers of 5 (and hence powers of 10).
DPatrick (20:08:20)
If we check a=b=624 and c=758, we get:
DPatrick (20:08:33)
[624/5] + [624/25] + [624/125] = 124 + 24 + 4 = 152.
[758/5] + [758/25] + [758/125] + [758/625] = 151 + 30 + 6 + 1 = 188.
DPatrick (20:08:39)
So there are 152+152+188 = 492 factors of 5. Better!
DPatrick (20:09:09)
Now we can eliminate (C)-(E) and we're left with (A) and (B).
DPatrick (20:09:14)
At this point I might be tempted to guess (B) and move on.
dimak11214 (20:09:25)
How do you know for sure that 492 it the lest amount?
DPatrick (20:10:02)
That's the question...how do we know [b]for sure[/b] that there's no a,b,c that gives 489 (choice (A))?
DPatrick (20:10:33)
For an arbitrary a,b,c, how many powers of 5 do we have?
me@home (20:10:32)
logically, no other values could possibly be lower.
4everwise (20:10:37)
as you make one of a,b, and c smaller, another gets larger
DPatrick (20:11:04)
I'd be pretty wary of arguments like that.
DPatrick (20:11:44)
We can prove it a lot more rigorously.
DPatrick (20:11:55)
(Note: on the AMC, of course you don't have to [b]prove[/b] anything.)
DPatrick (20:12:23)
For an arbitrary a,b,c, how many power of 5 do we have?
For an arbitrary a,b,c, we have this many powers of 5:
[a/5] + [a/25] + [a/125] + [a/625]
+ [b/5] + [b/25] + [b/125] + [b/625]
+ [c/5] + [c/25] + [c/125] + [c/625]
DPatrick (20:12:36)
What happens if we add the columns?
DPatrick (20:13:02)
We have use the identity [x] + [y] + [z] >= [x+y+z] - 2. (This is true since the fractional parts of x,y,z always add to some number less than 3.)
anniesez (20:13:01)
a+b+c=2006....
DPatrick (20:13:32)
Indeed, so [a/5]+[b/5]+[c/5] >= [2006/5] - 2 = 399.
DPatrick (20:14:02)
Similarly the other columns add to at least 78, 14, and 1.
DPatrick (20:14:11)
So the best we can do is 399+78+14+1 = 492.
DPatrick (20:14:25)
Now we're [b]sure[/b] that we found the best possible answer!
DPatrick (20:14:31)
(B) 492
DPatrick (20:14:46)
Let's go to #23 now:
DPatrick (20:14:52)

DPatrick (20:14:54)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-18527463.gif
DPatrick (20:15:07)

DPatrick (20:15:11)
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/e3fa96a13b9ac173ac22f196b7307308.png
DPatrick (20:15:25)
Any ideas?
alan (20:15:28)
rotation!
DPatrick (20:16:05)
There are some very clever solutions involving rotations and/or reflections.
DPatrick (20:16:20)
I'll get to those later, but for now let's assume we're not that clever (I wasn't when I first did this problem).
me@home (20:15:54)
square s
DPatrick (20:16:52)
Yes, one thing to note is that we're probably going to want to find s^2 rather than s.
DPatrick (20:17:02)
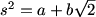
DPatrick (20:17:17)
That might suggest a couple of different tactics.
perfectnumber628 (20:17:24)
s^2 is twice the area of the triangle
DPatrick (20:17:52)
That's one good observation, and if you play around with this enough it might lead you to one of the clever rotation or reflection solutions.
DPatrick (20:18:12)
But again, let's suppose we're not clever and we just want a grind-it-out solution.
DPatrick (20:18:22)
Where else do we often see an s^2 term?
4everwise (20:18:32)
pythagoras
topaz (20:18:32)
pythagorean
mna851 (20:18:36)
Pythagorean theorem
DPatrick (20:18:57)
Certainly -- but what's Pythagorean's more flexible cousin?
alan (20:18:28)
law of cosines
4everwise (20:19:04)
law of cosines
DPatrick (20:19:21)
Yes -- we can bash this problem with the Law of Cosines.
DPatrick (20:19:34)
It is possible, but a bit messy!
DPatrick (20:19:50)
(this is how Richard Rusczyk and I did it when we first saw the problem!)
4everwise (20:19:24)
maybe we'd let central angles be variables
4everwise (20:19:38)
and express the other sides in terms of the angles and sides
DPatrick (20:20:16)
We could, but we don't have much information about those angles.
DPatrick (20:20:27)
We do, however, have a nice right angle sitting in the corner.
DPatrick (20:20:35)

DPatrick (20:20:39)
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/829df2f1e214dccc149c9251fe00ac5d.png
DPatrick (20:20:52)
Now we can apply the Law of Cosines on triangles PBC and PAC (remember s=AC=BC):
DPatrick (20:21:01)
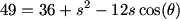
DPatrick (20:21:03)
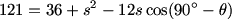
4everwise (20:21:27)
would it help to change that to sin theta?
alan (20:21:40)
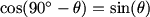
DPatrick (20:21:52)
It would help [b]a lot[/b]!
DPatrick (20:22:08)
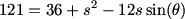
anniesez (20:21:28)
subtract them?
me@home (20:22:13)
subtract equations
DPatrick (20:22:34)
Subtracting them gets rid of the s^2, which is what we don't want to get rid of.
DPatrick (20:22:44)
I'd much rather get rid of the angle.
4everwise (20:22:45)
the trig functions
topaz (20:22:46)
isolate the trig and square
4everwise (20:22:54)
sin^2x+cos^2x=1
DPatrick (20:23:09)
Right. We want to exploit sin^2 + cos^2 = 1.
DPatrick (20:23:16)
We can solve for the cosine and sine:
perfectnumber628 (20:23:16)
maybe move the sin or cos to one side of the equation
DPatrick (20:23:32)
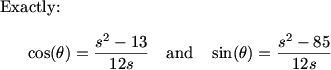
DPatrick (20:23:50)
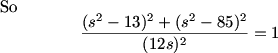
DPatrick (20:24:02)
Now we can solve for s^2!
4everwise (20:24:08)
yay
me@home (20:24:09)
amazing
DPatrick (20:24:34)
You might want a calculator for this part, though... :)
DPatrick (20:24:42)

DPatrick (20:25:03)
So you hit it with the quadratic formula:
DPatrick (20:25:10)
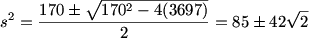
DPatrick (20:25:24)
So the answer is 85+42 = 127, choice (E).
dimak11214 (20:25:39)
wow very nice.
DPatrick (20:25:52)
And it didn't really require us to be clever.
me@home (20:25:45)
can you show the clever way??
DPatrick (20:26:13)
Sure...as I said, there are some very clever solutions using rotations and/or reflections.
DPatrick (20:26:24)
My favorite (of the ones I've seen) is to rotate the whole picture 90 degrees counterclockwise around point C:
DPatrick (20:26:33)
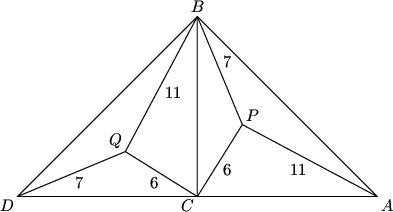
DPatrick (20:26:39)
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/ad593ac1d31ab66149a47bc459850adf.png
DPatrick (20:26:47)
Note that P rotates to point Q, and B rotates to point D.
perfectnumber628 (20:26:54)
QPC is a right angle
DPatrick (20:27:11)
I think you meant QCP, but right idea.
DPatrick (20:27:26)
So then the length of PQ is 6*sqrt(2).
DPatrick (20:27:41)
Then you need a clever observation.
DPatrick (20:28:04)
What's triangle QPB?
alan (20:28:06)
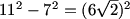
DPatrick (20:28:21)
Yes. Magic.
DPatrick (20:28:24)
QPB is a right triangle.
DPatrick (20:28:49)
In particular, angle BPC is 135 degrees: 90 from BPQ + 45 from QPC.
DPatrick (20:29:05)
So now you can do an easy Law of Cosines calculation using triangle BPC to find length BC.
me@home (20:29:17)
wow that's tricky...
DPatrick (20:29:35)
Indeed, it takes really good imagination to come up with this solution.
DPatrick (20:29:50)
There's another nice solution posted on the message board.
DPatrick (20:30:00)
Let's move on to #24.
DPatrick (20:30:07)
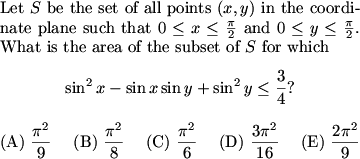
DPatrick (20:30:09)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-144896884.gif
DPatrick (20:30:31)
What do we do here?
DPatrick (20:31:08)
First of all, it should be clear (I hope) that to find this region, we need to solve the equality:
DPatrick (20:31:13)
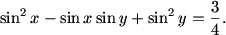
frodo (20:30:28)
Quadratic with sinx
DPatrick (20:31:54)
Right, we can think of this as a quadratic equation, and use the quadratic formula to solve for one sine in terms of the other.
DPatrick (20:32:09)
(I happened to do it the opposite way as frodo suggested, but it makes no difference whatsoever.)
DPatrick (20:32:17)
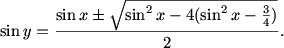
DPatrick (20:32:40)
But what is that term inside the radical?
Bictor717 (20:33:12)
3cos^2(x)
perfectnumber628 (20:33:12)
3-3sin^2(x)=3cos^2(x0
JHu (20:33:22)
3(cos^2(x))
DPatrick (20:33:48)
RIght! The term inside the square root is 3(1-sin^2 x).
DPatrick (20:34:00)
So it's just 3 cos^2 x.
DPatrick (20:34:10)
Then we can pull the cosine outside the square root (since 0 <= x <= pi/2, everything is positive):
DPatrick (20:34:17)
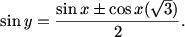
DPatrick (20:34:31)
What can we do with this?
frodo (20:34:43)
Angle sum.
DPatrick (20:34:58)
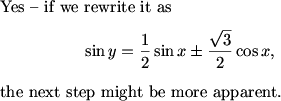
DPatrick (20:35:10)
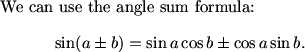
DPatrick (20:35:23)
If there's one nontrivial trig formula that you should learn, this is it.
topaz (20:35:15)
sin(x+pi/3)
JHu (20:35:38)
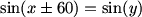
DPatrick (20:36:04)
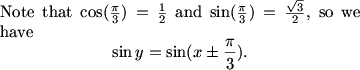
DPatrick (20:36:21)
(I'd stick with radians since the original problem is in terms of radians)
DPatrick (20:36:36)
So how do we graph this?
frodo (20:36:44)
DPatrick (20:37:09)
Tempting...
DPatrick (20:37:14)
...but sin(a)=sin(b) doesn't necessarily mean that a=b.
DPatrick (20:37:45)
We might have a = pi/2 - b.
DPatrick (20:38:11)
Certainly there are two separate cases we have to consider.
DPatrick (20:39:08)
If sin(y) = sin(x - pi/3), we can safely conclude that y = x - pi/3, because of the restriction on the range of x and y.
DPatrick (20:39:17)
But if sin(y) = sin(x + pi/3), that's another story.
DPatrick (20:39:34)
Certainly y = x + pi/3 is possible, but what else is possible?
frodo (20:37:50)
a+b=pi
DPatrick (20:40:16)
Yes, good correction! sin(a) = sin(b) might mean a = pi - b, not pi/2 as I wrote earlier.
perfectnumber628 (20:40:13)
y=pi-(x+pi/3)
DPatrick (20:40:37)
Right, we might have y = 2pi/3 - x.
DPatrick (20:40:47)
So, we have 3 line segments that we can graph in our square.
DPatrick (20:40:53)

DPatrick (20:40:56)
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/97759595fe323faa64c462e2417a40d3.png
DPatrick (20:41:26)
Which region do we want: the pentagon or the three triangles (or some mix of them)?
Teki-Teki (20:41:47)
pentagon
topaz (20:41:51)
the pentagon
DPatrick (20:42:11)
Yes: you can test points in each region and see that it's the pentagon that we want.
DPatrick (20:42:36)
...which we compute by taking the entire square and subtracting the three triangles.
DPatrick (20:42:47)
Note that the two little triangles are each 1/18th of the square, and the big triangle in upper-right is 2/9th of the square.
DPatrick (20:43:08)
So the pentagon makes up what's left, which is 2/3 of the square.
DPatrick (20:43:30)
And to finish, the area of the square is (pi^2)/4, so 2/3 of that is (pi^2)/6, and the answer is (C).
4everwise (20:43:31)
can't we just add the area of the rectangle and the 45,45,90 triangle?
DPatrick (20:44:05)
Yes, we could have done that instead, draw the line from (0,pi/3) to (pi/3,0) and compute the areas of the resulting rectangle and triangle.
DPatrick (20:44:15)
Finally, we do #25 on the 12B.
DPatrick (20:44:21)
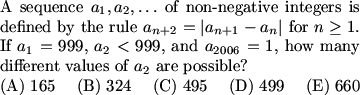
DPatrick (20:44:25)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-18235600.gif
DPatrick (20:44:47)
Those answer choices are a bit scary.
DPatrick (20:45:02)
What do we know about this sequence?
frodo (20:45:16)
Find a_(n+3) in terms for a_(n+1) and a_n.
DPatrick (20:45:43)
That's often what we try to do, but with all the absolute values floating around, it's going to be a nightmaer.
DPatrick (20:45:47)
...and a nightmare.
DPatrick (20:46:16)
Plus, since we know there are going to be *lots* of a_2's that work (based on the answer choices), we're probably better off looking for general patterns.
ssskier (20:46:08)
First we have to check out parity
DPatrick (20:46:33)
Parity is a good place to begin.
DPatrick (20:46:37)
What does parity tell us?
ssskier (20:46:43)
a_2 is odd
frodo (20:47:01)
a_n=a_(n+3)
DPatrick (20:47:18)
How come?
DPatrick (20:47:24)
(And I assume frodo means mod 2)
frodo (20:47:30)
Yes.
DPatrick (20:48:19)
We can just list the parity pattern.
quantum leap (20:48:21)
parity?
DPatrick (20:48:37)
Sorry -- when I say ""parity"", I basically mean ""odd"" or ""even"".
DPatrick (20:48:59)
So if a_1 and a_2 are both odd, the pattern goes OOEOOEOOEOOEOOE..., where O is odd and E is even.
DPatrick (20:49:13)
If a_1 is odd and a_2 is even, the pattern goes OEOOEOOEOOEO...
DPatrick (20:49:31)
So the parity repeats every 3rd term.
DPatrick (20:49:57)
Since we need a_2006 to be odd, we can't have the second pattern (since that pattern makes a_2006 even).
DPatrick (20:50:02)
So a_2 must be odd.
DPatrick (20:50:37)
What else can we do?
me@home (20:50:34)
can you use similar logic mod 3??
DPatrick (20:51:02)
Perhaps....what happens if a_2 is a multiple of 3?
perfectnumber628 (20:51:18)
then all terms are multiples of 3
Bictor717 (20:51:21)
all terms are multiples of 3
DPatrick (20:51:29)
Aha, good!
DPatrick (20:51:44)
Since the difference of two multiples of 3 is also a multiple of 3, if a_2 is a multiple of 3, then every term is.
DPatrick (20:51:55)
(since a_1 is too)
DPatrick (20:52:15)
So since we eventually have to reach 1 (which is *not* a multiple of 3), we know that a_2 cannot be a multiple of 3.
alan (20:52:27)
so only odd numbers relatively prime to 999 will work...
ssskier (20:52:28)
Same with all other primes
DPatrick (20:52:54)
Right. What's the prime factorization of 999?
4everwise (20:53:10)
3^3*37
frodo (20:53:13)
3^3*37
me@home (20:53:13)
3^3 * 37
perfectnumber628 (20:53:15)
3^3 (37)
ssskier (20:53:16)
3^3*37
DPatrick (20:53:34)
Right, so a_2 cannot be a multiple of 37 as well.
DPatrick (20:53:46)
How many odd integers less than 999 does that exclude?
og4life_42592 (20:54:06)
499
DPatrick (20:54:21)
We start with 499 odd integers less than 999.
DPatrick (20:54:27)
How many of those are multiples of 3 or 37.
DPatrick (20:54:30)
?
ssskier (20:54:19)
166+13-4
DPatrick (20:55:12)
Precisely. There are 166 multiples of 3 and 13 multiples of 37, but 4 of them are multiples of 3*37=111.
DPatrick (20:55:24)
So the number of odd positive integers less than 999 that are multiples of 3 or 37 are 166+13-4=175.
DPatrick (20:55:39)
So 499-175=324 of them are relatively prime to 999.
DPatrick (20:55:50)
This just happens to be answer choice (B).
DPatrick (20:56:03)
At this point we've definitely eliminated (C),(D), and (E), but the answer might still be (A): the 324 possible values for a_2 that we've got *might* all work, but we don't know that for a fact yet.
me@home (20:56:03)
how do we know to stop?
DPatrick (20:56:42)
Good question. Is there a way that we can show that all of the 324 numbers that we have left all work?
DPatrick (20:57:39)
Once again, as with #22 earlier, at this point I'd be awfully tempted to just go with answer (B), but we can in fact [b]prove[/b] that all these numbers work.
DPatrick (20:57:50)
What do we know about the size of each term, relative to the size of the previous two terms?
me@home (20:58:05)
its is smaller?
4everwise (20:58:09)
smaller
DPatrick (20:58:25)
More specifically, smaller than what?
Bictor717 (20:58:28)
its smaller than the larger of the two
DPatrick (20:58:37)
Right.
DPatrick (20:58:42)
a_{n+2} must be strictly smaller than the larger of a_{n+1} and a_n, as long as a_{n+1} and a_n are positive.
DPatrick (20:59:04)
We know that a_1 and a_2 are both positive (duh).
DPatrick (20:59:11)
This means that a_3 <= 998, a_5 <= 997, and so on, at least until we hit a 0.
DPatrick (20:59:49)
So either we hit a 0 at some point, or eventually we get to a_1997 <= 1 and a_1999 = 0.
DPatrick (20:59:56)
In any event, we hit 0 somewhere before the 2006th term.
DPatrick (21:00:06)
What happens when we get to 0?
Bictor717 (21:00:27)
terms are ""reflected""
ssskier (21:00:40)
The sequence cycles through 1,1,0
DPatrick (21:00:52)
Right. We can only get a 0 if the two previous terms were equal.
DPatrick (21:00:57)
So the sequence cycles kk0kk0kk0kk0kk0.... for some positive integer k.
DPatrick (21:01:10)
But because of our relatively prime condition, k must be 1.
DPatrick (21:01:28)
So all of our previously found a_2 work (those that are odd and relatively prime to 999), and the answer is (B) 324.
DPatrick (21:01:56)
In my estimation, 21 through 25 on this test were very hard compared to previous contests.
DPatrick (21:02:06)
Before we wrap up:
DPatrick (21:02:22)
We will be having a special AIME Problem Seminar during the weekend of March 4th and 5th (the weekend before the AIME).
DPatrick (21:02:38)
The seminar will meet for 3 hours each day and work through old AIME problems.
DPatrick (21:02:46)
More information is on the message board.
Hello and welcome to the 2006 AMC 10B/12B Math Jam!
DPatrick (19:01:51)
Before we get started I would like to take a moment to explain our virtual classroom to those who have not previously participated in a Math Jam or one of our online classes.
DPatrick (19:02:01)
The classroom is moderated meaning that students can type into the classroom, but only the moderators can choose a comment to drop into the classroom. This helps keep the class organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read. Also, only moderators can enter into private chats with other people in the classroom.
DPatrick (19:02:17)
Additionally, the virtual classroom is LaTeX enabled. LaTeX allows users to make nice equations and other math expressions. If you would like to learn how to write in LaTeX, click on the tab on the left side panel of our website and there is a tutorial and reference guide there.
DPatrick (19:02:29)
Using LaTeX in the virtual classroom is slightly different than using it on the message board or in a LaTeX editor. If anything you type up in a post that uses LaTeX then you must use a semicolon (;) to begin your post. For example, if you type
DPatrick (19:02:35)
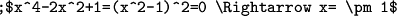
DPatrick (19:02:41)
This message will look like this when posted in the classroom:
DPatrick (19:02:50)
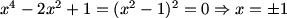
DPatrick (19:03:01)
Just remember, if your post uses LaTeX, use the semicolon (;) to begin your post!
DPatrick (19:03:12)
Lastly, some of the problems and diagrams in today's discussion are a bit large. I will generally post a link to the problems and diagrams, so that you can open them in a separate window. You should be able to just click on the link. You might have to hold down the Ctrl key while clicking. If this doesn't work, you may need to disable your popup blocker.
DPatrick (19:03:26)
You can also widen the chat window by dragging the vertical bar which separates the chat from the list of usernames.
DPatrick (19:03:40)
For those of you new to our AMC Math Jams, what we'll be doing today is working through detailed solutions of Problems 21-25 on the AMC 10B and 12B. A nice feature this year is that all but one of problems 21-25 on the 10B were also problems on the 12B.
DPatrick (19:04:02)
Let's start with #21 of the 10B, which is also #17 on the 12B.
DPatrick (19:04:05)

DPatrick (19:04:09)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-168846628.gif
DPatrick (19:04:38)
(As I mentioned above, you can click the link to popup the problem in a separate window, which is handy for following along as we work though the solution.)
DPatrick (19:04:55)
How can we begin on this problem?
Kakashi (19:04:47)
you can roll (1,6) (2,5) (3,4) (4,3) (5,2) (6,1)
eryaman (19:04:56)
find the probability of each number, then combos 1/6, 2/5, 3/4, 6/1, 5/2, 4/3
DPatrick (19:05:19)
Right, first we can observe that there are six ways it can happen: 1-6, 2-5, 3-4, 4-3, 5-2, and 6-1.
DPatrick (19:05:39)
So we can find the probability for each pair, then sum them up.
mna851 (19:05:09)
Set the probability of rolling a 1 euqal to p
DPatrick (19:06:07)
OK, let p denote the probability of rolling a 1 on one die.
DPatrick (19:06:12)
Then what are the probabilities of the other numbers on the die?
The Zuton Force (19:06:35)
2p 3p 4p 5p 6p
eryaman (19:06:39)
2p, 3p, 4p, 5p, 6p
mna851 (19:06:39)
2p, 3p, 4p, 5p, 6p
DPatrick (19:06:50)
Right: the probability of rolling a 2 is 2p, of rolling a 3 is 3p, and so on.
Bictor717 (19:06:06)
The sum of the probabilities is 1
DPatrick (19:07:06)
Exactly -- the sum of the probabilities of the 6 sides must sum to 1.
DPatrick (19:07:14)
Therefore, we can solve for p.
Thorn (19:07:13)
So we have p + 2p + 3p + 4p + 5p + 6p = 1
perfectnumber628 (19:07:10)
p=1/21
DPatrick (19:07:31)
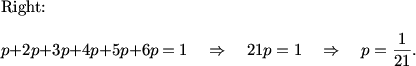
DPatrick (19:07:44)
So the probability of rolling a 1 is 1/21, of rolling a 2 is 2/21, and so on.
Thorn (19:07:48)
The rest is just arithmetic.
DPatrick (19:08:08)
Yep -- now we can sum up the six different ways of rolling a 7.
eryaman (19:08:12)
so 2((1/21)(6/21)+(2/21)(5/21)+(3/21)(4/21))
DPatrick (19:08:49)
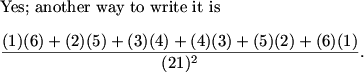
DPatrick (19:09:17)
This simplifies to 56/(21)^2 = 8/63. So the answer is (C).
DPatrick (19:10:09)
Next is #22 on the 10B, which is also #14 on the 12B.
DPatrick (19:10:17)

DPatrick (19:10:21)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-105292725.gif
DPatrick (19:10:45)
We need to translate the words into a mathematical formula that we can deal with. What's the formula?
jli (19:10:29)
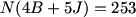
The Zuton Force (19:11:07)
N(4B+5J)=253
perfectnumber628 (19:11:11)
N(4B+5J)=253
DPatrick (19:11:24)
Each sandwich costs 4B + 5J cents to make, and there are N sandwiches which altogether cost 253 cents.
DPatrick (19:11:36)
So N(4B+5J) = 253.
DPatrick (19:11:40)
Now what?
demonface (19:11:18)
the factors of 253 is 11 and 23
jiangwei (19:11:43)
253=11*23
mna851 (19:11:43)
253=23*11
jli (19:11:43)
253=11*23
Kakashi (19:11:47)
N, B, J are all integers
DPatrick (19:12:06)
Yes, since everything in sight is a positive integer, both N and 4B+5J must be factors of 253.
perfectnumber628 (19:11:38)
n is 1, 11, 23, or 253
DPatrick (19:12:37)
Could N be either 1 or 253?
The Zuton Force (19:12:35)
n > 1
eryaman (19:12:42)
perfectnumber: the problem gives you that N>1
DPatrick (19:13:02)
Right, so we can rule that out.
DPatrick (19:13:05)
Could N be 253?
perfectnumber628 (19:13:02)
no, n>1 and 4B+5J will be greater than 1
DPatrick (19:13:40)
4B+5J cannot be 1 either (since B and J are positive), so N and 4B+5J must be 11 and 23 (in either order).
mel (19:12:40)
We know that multiples of 4 and 5 cannot sum to 1 or 11. So we try to get it to sum to 23.
demonface (19:12:46)
so we find out whether adding 4 and 5s can make 23 or 11
The Zuton Force (19:14:01)
you need at least one J and one B... once you're already at 9, you can't get to 11
DPatrick (19:14:14)
Yes, a little trial-and-error tells us that 4B+5J cannot equal 11 if B and J are positive integers, so we must have 4B + 5J = 23 and N = 11.
jiangwei (19:12:51)
B=2, J=3
eryaman (19:14:22)
4(2)+5(3)=23
perfectnumber628 (19:14:25)
B=2 and J=3
DPatrick (19:14:45)
Guess-and-check then gives B=2 and J=3.
DPatrick (19:14:50)
So how do we finish?
The Zuton Force (19:14:53)
15*11 = 165 -> $1.65
mna851 (19:14:56)
So each jelly sandwich costs 15 cents and since there a 11 of them the total cost is 15*11
DPatrick (19:15:14)
Yes: the cost of jam used is N(5J) = 11(15) = 165 cents, or $1.65. Answer (D).
DPatrick (19:15:49)
This is a simple example of a [b]Diophantine equation[/b]: an equation in which we're looking for integer solutions.
DPatrick (19:16:02)
Often, as in this case, prime factors are the key.
DPatrick (19:16:09)
#23 on the 10B is next (this problem did not appear on the 12B).
DPatrick (19:16:17)

DPatrick (19:16:28)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-198888500.gif
DPatrick (19:16:41)

DPatrick (19:16:51)
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/dda940a97180e4ee2e702f8a762dc922.png
DPatrick (19:17:07)
Any ideas?
mna851 (19:17:28)
Use the ratio of the bases and heights
jli (19:17:32)
draw the other line froom the vertex through the middle point
DPatrick (19:17:43)
These are two good ideas.
DPatrick (19:17:57)
We probably want to exploit the ""same base"" or ""same height"" principle, which states that the ratio of areas of two triangles with the same base (or same height) is proportional to the ratio of their heights (or bases).
DPatrick (19:18:16)
But that quadrilateral is ugly to work with.
DPatrick (19:18:28)
We can split it up into two triangles (I'm also going to label the points and the two new triangles for our convenience):
DPatrick (19:18:38)

DPatrick (19:18:40)
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/0a9a6fbe5583dae83c2a8b2def5bcc19.png
DPatrick (19:18:51)
What are some ratios of areas that we can now state?
DPatrick (19:20:05)
For example, triangles FDA and FDB share a height from F down to base AB.
DPatrick (19:20:37)
So the areas of FDA and FDB have the same ratio as the bases AD and AB.
DPatrick (19:21:10)
Is there another pair of triangles that have the same height and also have bases AD and AB?
eryaman (19:21:11)
AD/DB=3/x
DPatrick (19:21:30)
Right -- that's from our first pair of triangles.
DPatrick (19:21:41)
Is there another pair with ratio AD/DB?
Ars (19:22:07)
ADC and CDB
topaz (19:22:15)
ADC and BDC
DPatrick (19:22:44)
Good, both triangle ADC and BDC have the same height from C down to base AB.
DPatrick (19:23:03)
So the ratio of the areas of ADC and BDC equals the ratio of the bases AD and DB.
jli (19:22:19)
10/(x+y+7)
DPatrick (19:23:28)
Right, we get AD/DB = 10/(x+y+7) using triangles ADC and BDC.
DPatrick (19:23:35)
This gives us our first equation:
DPatrick (19:23:48)
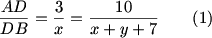
DPatrick (19:24:23)
Now let's try using this ""same height"" principle on triangles with bases CE and EB. What triangles can we use?
eryaman (19:24:37)
FBE and FEC
perfectnumber628 (19:24:41)
CFE and EFB
DPatrick (19:25:04)
Good, FEB and FEC share a height from F to base BC.
DPatrick (19:25:16)
So what is BE/EC equal to for these triangles?
shinwoo (19:25:36)
y/7
eryaman (19:25:39)
y/7
DPatrick (19:25:52)
Yep: BE/EC is the ratio of the areas, which is y/7.
DPatrick (19:26:07)
Is there another pair of triangles sharing a height to bases BE and EC?
perfectnumber628 (19:26:17)
AEC and AEB
topaz (19:26:20)
ABE and AEC
DPatrick (19:26:37)
Yes: AEB and AEC share a height from F down to BE and EC.
DPatrick (19:26:47)
What's the ratio of BE/EC for these triangles?
eryaman (19:27:14)
(3+x+y)/14
DPatrick (19:27:41)
Yes, it's the ratio of the areas of AEB and AEC, which is (3+x+y)/14.
DPatrick (19:27:47)
This gives us our second equation:
DPatrick (19:27:52)
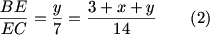
DPatrick (19:28:03)
What next?
eryaman (19:28:15)
so we have two equations, two variables, then i guess we could solve for the varialbes
jli (19:28:15)
system of 2 equations
DPatrick (19:28:47)
Yes, we can take equations (1) and (2) and set up a system of two equations in two variables.
DPatrick (19:28:58)
I would get rid of the denominators before doing anything else.
DPatrick (19:29:22)
...and move the x and y terms to one side of each equation, and the constant to the other.
DPatrick (19:29:35)
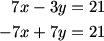
me@home (19:29:50)
now add the equations
DPatrick (19:30:16)
Yes, when written this way, solving is a breeze. We can add them to get 4y = 42.
eryaman (19:29:51)
so y=10.5
jli (19:30:04)
y=10.5
me@home (19:30:16)
4y=42, y=10.5
DPatrick (19:30:35)
So what's x, and what's the final answer?
perfectnumber628 (19:30:38)
x=7.5
DPatrick (19:30:59)
Plugging back in gives 7x=21+63/2=105/2, so x=15/2.
jli (19:31:00)
18
DPatrick (19:31:15)
So x+y = 18. Answer (D).
DPatrick (19:32:00)
The key step was using the ""same base/same height"" principle: that if two triangles share a base (or a height), then we can write a ratio of their areas in terms of a ratio whichever one (base or height) that they don't share.
DPatrick (19:32:13)
This is pretty common in problems involving areas of triangles but not much else (like this one).
DPatrick (19:32:29)
Next is #24 on the 10B, which is #15 on the 12B.
DPatrick (19:32:34)

DPatrick (19:32:38)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-131275396.gif
DPatrick (19:32:46)

DPatrick (19:32:51)
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/7ef2a58a812bf43f5c031b799c4a7626.png
DPatrick (19:33:07)
How shall we proceed?
demonface (19:33:03)
lets draw a rectangle
4everwise (19:33:15)
draw segment from O parallel to AD to meet DP
demonface (19:33:17)
from o to the middle of dp and cp
DPatrick (19:33:40)
We almost certainly need to drop perpendiculars from O to PD and PC. Let's label the new points X and Y.
DPatrick (19:33:49)

DPatrick (19:33:52)
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/a3f6d9d84e7aa8f74f3ab930fe9cbf50.png
DPatrick (19:34:00)
This pretty much finishes the problem!
The Zuton Force (19:33:28)
then use the pythagorean theorem
4everwise (19:34:02)
Now we can use pythagoras to find OX
demonface (19:34:08)
6^2-2^2=32 so its 4rt2
DPatrick (19:34:35)
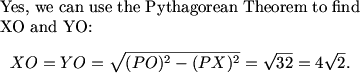
DPatrick (19:34:56)
(We note that ADXO is a rectangle (and so is OYCB), so DX = AO = 2 and PX = PD-DX = 2.)
DPatrick (19:35:14)
So now we can just add up the areas.
eryaman (19:35:13)
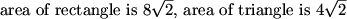
DPatrick (19:35:48)
Yes:
[ADXO] = [BOYC] = (AO)(OX) = 8*sqrt(2).
[OPX] = [OPY] = 1/2(PX)(OX) = 4*sqrt(2).
shinwoo (19:35:40)
the answer's B
og4life_42592 (19:35:53)
[b]answer's B[/b]
DPatrick (19:36:12)
So the area of the hexagon is 8sqrt(2)+4sqrt(2)+4sqrt(2)+8sqrt(2) = 24*sqrt(2), answer (B).
DPatrick (19:36:59)
Last on the 10B is #25, which is also #19 on the 12B.
DPatrick (19:37:04)

DPatrick (19:37:09)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-193805656.gif
DPatrick (19:37:44)
There's a lot of information to parse in this problem. When presented with a problem statement this complicated, I highly recommend reading it twice.
DPatrick (19:38:07)
For ease of referring to it, let's call the 4-digit number N.
DPatrick (19:38:30)
Are there any answers that we can eliminate right away?
demonface (19:37:31)
we know that since 9 and 2 are there, 6 is there too along with 4
dimak11214 (19:38:41)
6
Ars (19:38:45)
4 and 6
danthemanvt (19:38:48)
it must be divisible by 2 and 3 since they aren't in the list, so its divisib;e by6
mna851 (19:38:53)
4
DPatrick (19:39:20)
Yes, we know N is divisible by 2 and 3, so it must be divisible by 6.
DPatrick (19:39:37)
The answer also can't be 4, since if N is not divisible by 4, then it's also not divisible by 8.
DPatrick (19:39:51)
So the ""bad"" number (the only that N is not divisible by) must be 5, 7, or 8.
DPatrick (19:40:09)
Now what?
og4life_42592 (19:40:25)
plug in number's
pilot (19:40:32)
guess and check
DPatrick (19:40:46)
Meaning what exactly?
DPatrick (19:41:02)
Which number should we test first?
dimak11214 (19:40:50)
Would it help that the digits add up to 9.
DPatrick (19:41:32)
Definitely -- since N is divisible by 9, the two digits have to sum to 9. This narrows our possibilities for N considerably.
perfectnumber628 (19:41:23)
i tested 5
DPatrick (19:42:00)
5 is probably the best one to test, since the divisibilty by 5 condition is so strong.
DPatrick (19:42:10)
N is divisible by 5 if and only if the last digit is 5 or 0.
Kakashi (19:42:19)
cant be 5 cus its even
DPatrick (19:42:45)
Right, the last digit can't be 5, since we know that 2 divides N.
DPatrick (19:43:08)
So that leaves 9900 or 9090 as the only possibilities.
pilot (19:43:12)
so it must be 9900 or 9090 but neither of those work
DPatrick (19:43:29)
Specificially, why don't they work?
mna851 (19:43:30)
but 9900 can't be b/c the last digits wouldnt be the fatheres age
DPatrick (19:44:11)
Right -- we know that the last two digits are the father's age, and his age of ""00"" is absurd.
Impossible (19:44:08)
9090 isnt divisible by 4
DPatrick (19:44:36)
And 9090 can't work since it's not a multiple of 4 (which we know N has to be).
dimak11214 (19:44:35)
so 5 is out
DPatrick (19:45:01)
Yes, that's it: N cannot be divisible by 5, and hence (B) is the answer.
jiangwei (19:44:50)
5544
perfectnumber628 (19:45:15)
N could be 5544
DPatrick (19:45:38)
Right. We know that N is divisible by 7, 8, and 9, so N must be a multiple of 7*8*9 = 504.
DPatrick (19:45:44)
Then we can easily see that N = 11*504 = 5544 is the license plate.
DPatrick (19:46:11)
There are lots of ways to do this problem -- the way that we just worked through it is essentially the way that I first did it.
DPatrick (19:46:38)
You could have tried to find N directly (as I just did above) and gotten it that way too.
DPatrick (19:46:55)
Now we'll move on to the last 5 AMC 12B problems.
DPatrick (19:47:02)
We'll start with #21.
DPatrick (19:47:08)

DPatrick (19:47:16)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-19823188.gif
DPatrick (19:48:00)
The first thing I would do with this problem is sketch a picture.
DPatrick (19:48:07)

DPatrick (19:48:10)
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/5debecb8103f18cf264e5853c881f51a.png
eryaman (19:47:47)
if x and y are the sides, then xy=2006
DPatrick (19:48:33)
OK, let the two sides of the rectangle have lengths x and y.
DPatrick (19:48:43)
Then we're given that xy = 2006. We want to find 2(x+y).
Thorn (19:49:07)
Now, since B and D are foci, I would connect BD to draw the major axis of the ellopse.
eryaman (19:49:18)
we can draw and try to find the lengtsh of the major/minor axis
DPatrick (19:49:40)
Before we do that, to solve this problem, we need to know how an ellipse is described in terms of its foci.
DPatrick (19:49:48)
What exactly is an ellipse?
The Zuton Force (19:50:09)
distances from foci to a point on the elipse sum to a constant
eryaman (19:50:22)
the set of all points such that the sum of the distances from the foci is a certain number
DPatrick (19:50:34)
Exactly.
me@home (19:50:21)
the locus of points that a pencil attached to a string with enpoints at B,D
DPatrick (19:50:54)
Yes, this is a practical way to draw one (the length of the string is the sum of the distances to the two foci).
DPatrick (19:51:17)
So for any point P on the ellipse, the sum PB + PD is constant.
perfectnumber628 (19:51:07)
so x+y is the distance from the foci to any point on the ellipse
DPatrick (19:51:52)
Right! We could take the point A, and we get that this constant distance is PB + PD = x+y.
DPatrick (19:52:07)
So how can we use that to find the lengths of the axes of the ellipse?
DPatrick (19:52:28)
Let's do the easier axis first, which is the major axis (the axis that includes the two foci).
DPatrick (19:52:48)
What's its length?
perfectnumber628 (19:52:38)
the string length (x+y) equals the length of the major axis
Bictor717 (19:52:51)
2a=x+y
DPatrick (19:53:14)
Right. This is another basic fact about ellipses.
DPatrick (19:53:20)
The length of the major axis (the one including the foci) is just the common distance sum, so 2a = x+y.
DPatrick (19:53:31)
How do we find the other (minor) axis?
eryaman (19:52:15)
so if we draw lines from the foci to the ""top"" of the ellipse, then each line will have (x+y)/2
DPatrick (19:54:10)

DPatrick (19:54:14)
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/2662cb2341f3beb42e7bcd86006f2237.png
DPatrick (19:54:31)
Right.
DPatrick (19:54:44)
""d"" in this picture is the distance between the foci.
DPatrick (19:54:49)
But what is d?
alan (19:54:52)
d=√x2+y2
alan (19:55:03)
diagonal of the rectangle
perfectnumber628 (19:55:03)
d is the diagonal of the rectangle
duckpaladin88 (19:55:08)
d = square root of x^2 + y^2
DPatrick (19:55:21)
Exactly -- d is the diagonal of the rectangle.
eryaman (19:55:11)
pythag theorem...
DPatrick (19:55:45)
Right, we can use the Pythagorean Theorem to find b.
DPatrick (19:55:54)
(actually we can multiply by 2 to get rid of the fractions and find 2b instead):
DPatrick (19:56:04)
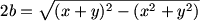
DPatrick (19:56:17)
How does this simplify?
anniesez (19:56:16)
so 2xy is left
eryaman (19:56:24)
so 2b = sqrt(2xy)
Teki-Teki (19:56:28)
2b = sqrt( 2xy )
me@home (19:56:28)
sqrt(2xy) = 2b
Ars (19:56:32)
2b=sqrt(2xy)
4everwise (19:56:37)
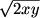
The Zuton Force (19:56:37)
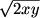
DPatrick (19:56:54)
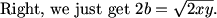
anniesez (19:56:23)
but that's 2006
Bictor717 (19:57:05)
xy=2006
DPatrick (19:57:20)
Yes! xy = 2006 is the area of the rectangle.
DPatrick (19:57:40)
So we can solve for b!
me@home (19:57:56)
sqrt(1003)
Impossible (19:58:00)
b=(1003)^(1/2)
anniesez (19:58:02)
b= sqrt 1003?
DPatrick (19:58:09)
Yes, b = sqrt(1003).
DPatrick (19:58:19)
We're very close now!
DPatrick (19:58:30)
What's a?
Bictor717 (19:58:29)
ab=2006
DPatrick (19:58:59)
Yes, the problem told us that the area of the ellipse was 2006pi, and it also (nicely!) told use that this area is pi*ab.
duckpaladin88 (19:59:32)
so a = 2*sqrt*1003
JHu (19:59:45)
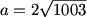
DPatrick (20:00:02)
Right, we can solve for a and get a = 2*sqrt(1003).
me@home (19:59:37)
a is half the perimeter!!
DPatrick (20:00:13)
Almost...
Bictor717 (20:00:13)
2a=x+y
DPatrick (20:00:29)
Right, so a is 1/4 of the perimeter.
4everwise (20:00:13)
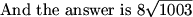
alan (20:00:34)
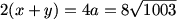
DPatrick (20:00:42)
And we're done! Choice (C).
DPatrick (20:01:27)
You had to know what it meant for something to be an ellipse to make any headway in this problem, but if you did know what an ellipse was, and drew the right picture, the problem was manageable.
DPatrick (20:01:51)
Now on to #22:
DPatrick (20:01:53)
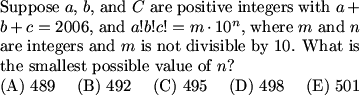
DPatrick (20:01:59)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-175196001.gif
DPatrick (20:02:18)
What are we [i]really[/i] trying to find here?
eryaman (20:02:32)
number of 5's
alan (20:02:38)
number of 5's
mna851 (20:02:38)
Three numbers whose factorials have the least factors of 5 in them
Thorn (20:02:43)
We are trying to count how many factors of 5 are in a!b!c!
DPatrick (20:02:58)
Right, since in factorials, powers of 10 are really determined by powers of 5, we're really looking to count the number of powers of 5 in a!b!c!.
DPatrick (20:03:29)
There are really only two reasonable guesses to try at this point for a,b,c.
jiangwei (20:02:29)
624, 624,
The Zuton Force (20:02:50)
We want to minimize the factors of 10, and hence the factors of 5. 625 has many powers of 5 because it is a power of 5, so setting a and b to 624 will cause you to loose several factors of 5 without inflating c.
alan (20:03:38)
624
topaz (20:03:48)
624...
DPatrick (20:04:39)
That's one very reasonable guess: to set a=b=624 and thus 758, for the reason that Zuton describes (since 625 has a lot of powers of 5 and thus should be avoided).
perfectnumber628 (20:04:09)
a, b, and c must be equal or close to each other if a!b!c! is small
DPatrick (20:05:10)
That's the other very reasonable guess: to make them as equal as possible: a=668 and b=c=669.
DPatrick (20:05:26)
Once we have a guess, how do we count the powers of 5?
Thorn (20:03:31)
To count how many factors of 5 are in N, we take N/5 + n/25 + N/125 + N/625
perfectnumber628 (20:05:44)
divide by 5, and 25, and 125
DPatrick (20:05:56)
Right.
Bictor717 (20:05:56)
floor function'd
DPatrick (20:06:08)
Exactly.
DPatrick (20:06:52)
The number of powers of 5 in N! is [N/5] + [N/25] + [N/125] + [N/625], where [x] means the floor function, or the largest integer less than or equal x.
dimak11214 (20:06:33)
668,669 has 495 5's
DPatrick (20:07:33)
Right, if we check our guess a=668 and b=c=669, we get
[668/5] + [668/25] + [668/125] + [668/625]
133 + 26 + 5 + 1 = 165.
DPatrick (20:07:44)
(669 doesn't add a power of 5).
DPatrick (20:07:52)
So that's 3*165 = 495 powers of 5 (and hence powers of 10).
DPatrick (20:08:20)
If we check a=b=624 and c=758, we get:
DPatrick (20:08:33)
[624/5] + [624/25] + [624/125] = 124 + 24 + 4 = 152.
[758/5] + [758/25] + [758/125] + [758/625] = 151 + 30 + 6 + 1 = 188.
DPatrick (20:08:39)
So there are 152+152+188 = 492 factors of 5. Better!
DPatrick (20:09:09)
Now we can eliminate (C)-(E) and we're left with (A) and (B).
DPatrick (20:09:14)
At this point I might be tempted to guess (B) and move on.
dimak11214 (20:09:25)
How do you know for sure that 492 it the lest amount?
DPatrick (20:10:02)
That's the question...how do we know [b]for sure[/b] that there's no a,b,c that gives 489 (choice (A))?
DPatrick (20:10:33)
For an arbitrary a,b,c, how many powers of 5 do we have?
me@home (20:10:32)
logically, no other values could possibly be lower.
4everwise (20:10:37)
as you make one of a,b, and c smaller, another gets larger
DPatrick (20:11:04)
I'd be pretty wary of arguments like that.
DPatrick (20:11:44)
We can prove it a lot more rigorously.
DPatrick (20:11:55)
(Note: on the AMC, of course you don't have to [b]prove[/b] anything.)
DPatrick (20:12:23)
For an arbitrary a,b,c, how many power of 5 do we have?
For an arbitrary a,b,c, we have this many powers of 5:
[a/5] + [a/25] + [a/125] + [a/625]
+ [b/5] + [b/25] + [b/125] + [b/625]
+ [c/5] + [c/25] + [c/125] + [c/625]
DPatrick (20:12:36)
What happens if we add the columns?
DPatrick (20:13:02)
We have use the identity [x] + [y] + [z] >= [x+y+z] - 2. (This is true since the fractional parts of x,y,z always add to some number less than 3.)
anniesez (20:13:01)
a+b+c=2006....
DPatrick (20:13:32)
Indeed, so [a/5]+[b/5]+[c/5] >= [2006/5] - 2 = 399.
DPatrick (20:14:02)
Similarly the other columns add to at least 78, 14, and 1.
DPatrick (20:14:11)
So the best we can do is 399+78+14+1 = 492.
DPatrick (20:14:25)
Now we're [b]sure[/b] that we found the best possible answer!
DPatrick (20:14:31)
(B) 492
DPatrick (20:14:46)
Let's go to #23 now:
DPatrick (20:14:52)

DPatrick (20:14:54)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-18527463.gif
DPatrick (20:15:07)

DPatrick (20:15:11)
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/e3fa96a13b9ac173ac22f196b7307308.png
DPatrick (20:15:25)
Any ideas?
alan (20:15:28)
rotation!
DPatrick (20:16:05)
There are some very clever solutions involving rotations and/or reflections.
DPatrick (20:16:20)
I'll get to those later, but for now let's assume we're not that clever (I wasn't when I first did this problem).
me@home (20:15:54)
square s
DPatrick (20:16:52)
Yes, one thing to note is that we're probably going to want to find s^2 rather than s.
DPatrick (20:17:02)
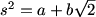
DPatrick (20:17:17)
That might suggest a couple of different tactics.
perfectnumber628 (20:17:24)
s^2 is twice the area of the triangle
DPatrick (20:17:52)
That's one good observation, and if you play around with this enough it might lead you to one of the clever rotation or reflection solutions.
DPatrick (20:18:12)
But again, let's suppose we're not clever and we just want a grind-it-out solution.
DPatrick (20:18:22)
Where else do we often see an s^2 term?
4everwise (20:18:32)
pythagoras
topaz (20:18:32)
pythagorean
mna851 (20:18:36)
Pythagorean theorem
DPatrick (20:18:57)
Certainly -- but what's Pythagorean's more flexible cousin?
alan (20:18:28)
law of cosines
4everwise (20:19:04)
law of cosines
DPatrick (20:19:21)
Yes -- we can bash this problem with the Law of Cosines.
DPatrick (20:19:34)
It is possible, but a bit messy!
DPatrick (20:19:50)
(this is how Richard Rusczyk and I did it when we first saw the problem!)
4everwise (20:19:24)
maybe we'd let central angles be variables
4everwise (20:19:38)
and express the other sides in terms of the angles and sides
DPatrick (20:20:16)
We could, but we don't have much information about those angles.
DPatrick (20:20:27)
We do, however, have a nice right angle sitting in the corner.
DPatrick (20:20:35)

DPatrick (20:20:39)
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/829df2f1e214dccc149c9251fe00ac5d.png
DPatrick (20:20:52)
Now we can apply the Law of Cosines on triangles PBC and PAC (remember s=AC=BC):
DPatrick (20:21:01)
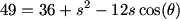
DPatrick (20:21:03)
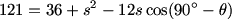
4everwise (20:21:27)
would it help to change that to sin theta?
alan (20:21:40)
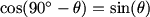
DPatrick (20:21:52)
It would help [b]a lot[/b]!
DPatrick (20:22:08)
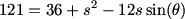
anniesez (20:21:28)
subtract them?
me@home (20:22:13)
subtract equations
DPatrick (20:22:34)
Subtracting them gets rid of the s^2, which is what we don't want to get rid of.
DPatrick (20:22:44)
I'd much rather get rid of the angle.
4everwise (20:22:45)
the trig functions
topaz (20:22:46)
isolate the trig and square
4everwise (20:22:54)
sin^2x+cos^2x=1
DPatrick (20:23:09)
Right. We want to exploit sin^2 + cos^2 = 1.
DPatrick (20:23:16)
We can solve for the cosine and sine:
perfectnumber628 (20:23:16)
maybe move the sin or cos to one side of the equation
DPatrick (20:23:32)
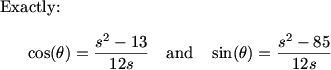
DPatrick (20:23:50)
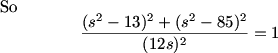
DPatrick (20:24:02)
Now we can solve for s^2!
4everwise (20:24:08)
yay
me@home (20:24:09)
amazing
DPatrick (20:24:34)
You might want a calculator for this part, though... :)
DPatrick (20:24:42)

DPatrick (20:25:03)
So you hit it with the quadratic formula:
DPatrick (20:25:10)
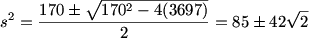
DPatrick (20:25:24)
So the answer is 85+42 = 127, choice (E).
dimak11214 (20:25:39)
wow very nice.
DPatrick (20:25:52)
And it didn't really require us to be clever.
me@home (20:25:45)
can you show the clever way??
DPatrick (20:26:13)
Sure...as I said, there are some very clever solutions using rotations and/or reflections.
DPatrick (20:26:24)
My favorite (of the ones I've seen) is to rotate the whole picture 90 degrees counterclockwise around point C:
DPatrick (20:26:33)

DPatrick (20:26:39)
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/ad593ac1d31ab66149a47bc459850adf.png
DPatrick (20:26:47)
Note that P rotates to point Q, and B rotates to point D.
perfectnumber628 (20:26:54)
QPC is a right angle
DPatrick (20:27:11)
I think you meant QCP, but right idea.
DPatrick (20:27:26)
So then the length of PQ is 6*sqrt(2).
DPatrick (20:27:41)
Then you need a clever observation.
DPatrick (20:28:04)
What's triangle QPB?
alan (20:28:06)
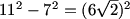
DPatrick (20:28:21)
Yes. Magic.
DPatrick (20:28:24)
QPB is a right triangle.
DPatrick (20:28:49)
In particular, angle BPC is 135 degrees: 90 from BPQ + 45 from QPC.
DPatrick (20:29:05)
So now you can do an easy Law of Cosines calculation using triangle BPC to find length BC.
me@home (20:29:17)
wow that's tricky...
DPatrick (20:29:35)
Indeed, it takes really good imagination to come up with this solution.
DPatrick (20:29:50)
There's another nice solution posted on the message board.
DPatrick (20:30:00)
Let's move on to #24.
DPatrick (20:30:07)
DPatrick (20:30:09)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-144896884.gif
DPatrick (20:30:31)
What do we do here?
DPatrick (20:31:08)
First of all, it should be clear (I hope) that to find this region, we need to solve the equality:
DPatrick (20:31:13)
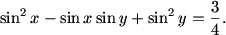
frodo (20:30:28)
Quadratic with sinx
DPatrick (20:31:54)
Right, we can think of this as a quadratic equation, and use the quadratic formula to solve for one sine in terms of the other.
DPatrick (20:32:09)
(I happened to do it the opposite way as frodo suggested, but it makes no difference whatsoever.)
DPatrick (20:32:17)
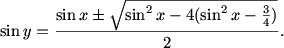
DPatrick (20:32:40)
But what is that term inside the radical?
Bictor717 (20:33:12)
3cos^2(x)
perfectnumber628 (20:33:12)
3-3sin^2(x)=3cos^2(x0
JHu (20:33:22)
3(cos^2(x))
DPatrick (20:33:48)
RIght! The term inside the square root is 3(1-sin^2 x).
DPatrick (20:34:00)
So it's just 3 cos^2 x.
DPatrick (20:34:10)
Then we can pull the cosine outside the square root (since 0 <= x <= pi/2, everything is positive):
DPatrick (20:34:17)
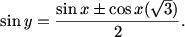
DPatrick (20:34:31)
What can we do with this?
frodo (20:34:43)
Angle sum.
DPatrick (20:34:58)
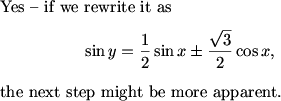
DPatrick (20:35:10)
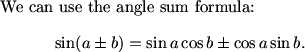
DPatrick (20:35:23)
If there's one nontrivial trig formula that you should learn, this is it.
topaz (20:35:15)
sin(x+pi/3)
JHu (20:35:38)
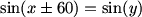
DPatrick (20:36:04)
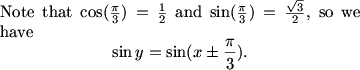
DPatrick (20:36:21)
(I'd stick with radians since the original problem is in terms of radians)
DPatrick (20:36:36)
So how do we graph this?
frodo (20:36:44)
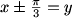
DPatrick (20:37:09)
Tempting...
DPatrick (20:37:14)
...but sin(a)=sin(b) doesn't necessarily mean that a=b.
DPatrick (20:37:45)
We might have a = pi/2 - b.
DPatrick (20:38:11)
Certainly there are two separate cases we have to consider.
DPatrick (20:39:08)
If sin(y) = sin(x - pi/3), we can safely conclude that y = x - pi/3, because of the restriction on the range of x and y.
DPatrick (20:39:17)
But if sin(y) = sin(x + pi/3), that's another story.
DPatrick (20:39:34)
Certainly y = x + pi/3 is possible, but what else is possible?
frodo (20:37:50)
a+b=pi
DPatrick (20:40:16)
Yes, good correction! sin(a) = sin(b) might mean a = pi - b, not pi/2 as I wrote earlier.
perfectnumber628 (20:40:13)
y=pi-(x+pi/3)
DPatrick (20:40:37)
Right, we might have y = 2pi/3 - x.
DPatrick (20:40:47)
So, we have 3 line segments that we can graph in our square.
DPatrick (20:40:53)

DPatrick (20:40:56)
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/97759595fe323faa64c462e2417a40d3.png
DPatrick (20:41:26)
Which region do we want: the pentagon or the three triangles (or some mix of them)?
Teki-Teki (20:41:47)
pentagon
topaz (20:41:51)
the pentagon
DPatrick (20:42:11)
Yes: you can test points in each region and see that it's the pentagon that we want.
DPatrick (20:42:36)
...which we compute by taking the entire square and subtracting the three triangles.
DPatrick (20:42:47)
Note that the two little triangles are each 1/18th of the square, and the big triangle in upper-right is 2/9th of the square.
DPatrick (20:43:08)
So the pentagon makes up what's left, which is 2/3 of the square.
DPatrick (20:43:30)
And to finish, the area of the square is (pi^2)/4, so 2/3 of that is (pi^2)/6, and the answer is (C).
4everwise (20:43:31)
can't we just add the area of the rectangle and the 45,45,90 triangle?
DPatrick (20:44:05)
Yes, we could have done that instead, draw the line from (0,pi/3) to (pi/3,0) and compute the areas of the resulting rectangle and triangle.
DPatrick (20:44:15)
Finally, we do #25 on the 12B.
DPatrick (20:44:21)
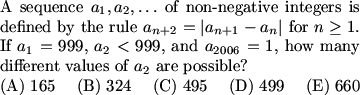
DPatrick (20:44:25)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-18235600.gif
DPatrick (20:44:47)
Those answer choices are a bit scary.
DPatrick (20:45:02)
What do we know about this sequence?
frodo (20:45:16)
Find a_(n+3) in terms for a_(n+1) and a_n.
DPatrick (20:45:43)
That's often what we try to do, but with all the absolute values floating around, it's going to be a nightmaer.
DPatrick (20:45:47)
...and a nightmare.
DPatrick (20:46:16)
Plus, since we know there are going to be *lots* of a_2's that work (based on the answer choices), we're probably better off looking for general patterns.
ssskier (20:46:08)
First we have to check out parity
DPatrick (20:46:33)
Parity is a good place to begin.
DPatrick (20:46:37)
What does parity tell us?
ssskier (20:46:43)
a_2 is odd
frodo (20:47:01)
a_n=a_(n+3)
DPatrick (20:47:18)
How come?
DPatrick (20:47:24)
(And I assume frodo means mod 2)
frodo (20:47:30)
Yes.
DPatrick (20:48:19)
We can just list the parity pattern.
quantum leap (20:48:21)
parity?
DPatrick (20:48:37)
Sorry -- when I say ""parity"", I basically mean ""odd"" or ""even"".
DPatrick (20:48:59)
So if a_1 and a_2 are both odd, the pattern goes OOEOOEOOEOOEOOE..., where O is odd and E is even.
DPatrick (20:49:13)
If a_1 is odd and a_2 is even, the pattern goes OEOOEOOEOOEO...
DPatrick (20:49:31)
So the parity repeats every 3rd term.
DPatrick (20:49:57)
Since we need a_2006 to be odd, we can't have the second pattern (since that pattern makes a_2006 even).
DPatrick (20:50:02)
So a_2 must be odd.
DPatrick (20:50:37)
What else can we do?
me@home (20:50:34)
can you use similar logic mod 3??
DPatrick (20:51:02)
Perhaps....what happens if a_2 is a multiple of 3?
perfectnumber628 (20:51:18)
then all terms are multiples of 3
Bictor717 (20:51:21)
all terms are multiples of 3
DPatrick (20:51:29)
Aha, good!
DPatrick (20:51:44)
Since the difference of two multiples of 3 is also a multiple of 3, if a_2 is a multiple of 3, then every term is.
DPatrick (20:51:55)
(since a_1 is too)
DPatrick (20:52:15)
So since we eventually have to reach 1 (which is *not* a multiple of 3), we know that a_2 cannot be a multiple of 3.
alan (20:52:27)
so only odd numbers relatively prime to 999 will work...
ssskier (20:52:28)
Same with all other primes
DPatrick (20:52:54)
Right. What's the prime factorization of 999?
4everwise (20:53:10)
3^3*37
frodo (20:53:13)
3^3*37
me@home (20:53:13)
3^3 * 37
perfectnumber628 (20:53:15)
3^3 (37)
ssskier (20:53:16)
3^3*37
DPatrick (20:53:34)
Right, so a_2 cannot be a multiple of 37 as well.
DPatrick (20:53:46)
How many odd integers less than 999 does that exclude?
og4life_42592 (20:54:06)
499
DPatrick (20:54:21)
We start with 499 odd integers less than 999.
DPatrick (20:54:27)
How many of those are multiples of 3 or 37.
DPatrick (20:54:30)
?
ssskier (20:54:19)
166+13-4
DPatrick (20:55:12)
Precisely. There are 166 multiples of 3 and 13 multiples of 37, but 4 of them are multiples of 3*37=111.
DPatrick (20:55:24)
So the number of odd positive integers less than 999 that are multiples of 3 or 37 are 166+13-4=175.
DPatrick (20:55:39)
So 499-175=324 of them are relatively prime to 999.
DPatrick (20:55:50)
This just happens to be answer choice (B).
DPatrick (20:56:03)
At this point we've definitely eliminated (C),(D), and (E), but the answer might still be (A): the 324 possible values for a_2 that we've got *might* all work, but we don't know that for a fact yet.
me@home (20:56:03)
how do we know to stop?
DPatrick (20:56:42)
Good question. Is there a way that we can show that all of the 324 numbers that we have left all work?
DPatrick (20:57:39)
Once again, as with #22 earlier, at this point I'd be awfully tempted to just go with answer (B), but we can in fact [b]prove[/b] that all these numbers work.
DPatrick (20:57:50)
What do we know about the size of each term, relative to the size of the previous two terms?
me@home (20:58:05)
its is smaller?
4everwise (20:58:09)
smaller
DPatrick (20:58:25)
More specifically, smaller than what?
Bictor717 (20:58:28)
its smaller than the larger of the two
DPatrick (20:58:37)
Right.
DPatrick (20:58:42)
a_{n+2} must be strictly smaller than the larger of a_{n+1} and a_n, as long as a_{n+1} and a_n are positive.
DPatrick (20:59:04)
We know that a_1 and a_2 are both positive (duh).
DPatrick (20:59:11)
This means that a_3 <= 998, a_5 <= 997, and so on, at least until we hit a 0.
DPatrick (20:59:49)
So either we hit a 0 at some point, or eventually we get to a_1997 <= 1 and a_1999 = 0.
DPatrick (20:59:56)
In any event, we hit 0 somewhere before the 2006th term.
DPatrick (21:00:06)
What happens when we get to 0?
Bictor717 (21:00:27)
terms are ""reflected""
ssskier (21:00:40)
The sequence cycles through 1,1,0
DPatrick (21:00:52)
Right. We can only get a 0 if the two previous terms were equal.
DPatrick (21:00:57)
So the sequence cycles kk0kk0kk0kk0kk0.... for some positive integer k.
DPatrick (21:01:10)
But because of our relatively prime condition, k must be 1.
DPatrick (21:01:28)
So all of our previously found a_2 work (those that are odd and relatively prime to 999), and the answer is (B) 324.
DPatrick (21:01:56)
In my estimation, 21 through 25 on this test were very hard compared to previous contests.
DPatrick (21:02:06)
Before we wrap up:
DPatrick (21:02:22)
We will be having a special AIME Problem Seminar during the weekend of March 4th and 5th (the weekend before the AIME).
DPatrick (21:02:38)
The seminar will meet for 3 hours each day and work through old AIME problems.
DPatrick (21:02:46)
More information is on the message board.
Copyright © 2025 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.









