Mock AIME 3 Pre 2005 Problems/Problem 14
Problem
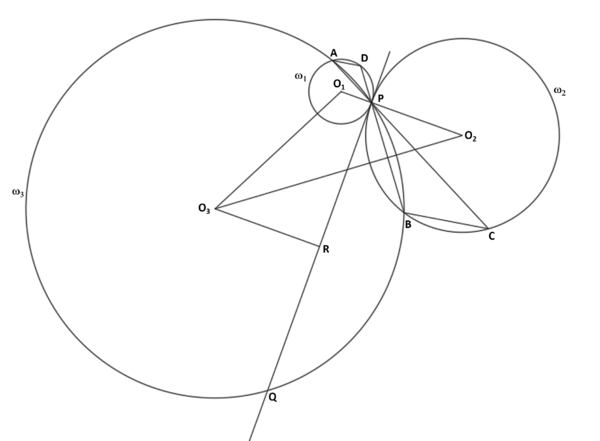
Circles ![]() and
and ![]() are centered on opposite sides of line
are centered on opposite sides of line ![]() , and are both tangent to
, and are both tangent to ![]() at
at ![]() .
. ![]() passes through
passes through ![]() , intersecting
, intersecting ![]() again at
again at ![]() . Let
. Let ![]() and
and ![]() be the intersections of
be the intersections of ![]() and
and ![]() , and
, and ![]() and
and ![]() respectively.
respectively. ![]() and
and ![]() are extended past
are extended past ![]() and intersect
and intersect ![]() and
and ![]() at
at ![]() and
and ![]() respectively. If
respectively. If ![]() and
and ![]() , then the area of triangle
, then the area of triangle ![]() can be expressed as
can be expressed as ![]() , where
, where ![]() and
and ![]() are positive integers such that
are positive integers such that ![]() and
and ![]() are coprime and
are coprime and ![]() is not divisible by the square of any prime. Determine
is not divisible by the square of any prime. Determine ![]() .
.
Solution
Let ![]() and
and ![]() be the centers of
be the centers of ![]() and
and ![]() respectively.
respectively.
Let point ![]() be the midpoint of
be the midpoint of ![]() . Thus,
. Thus, ![]() and
and ![]()
Let ![]() and
and ![]() be the radii of circles
be the radii of circles ![]() and
and ![]() respectively.
respectively.
Let ![]() and
and ![]() be the areas of triangles
be the areas of triangles ![]() and
and ![]() respectively.
respectively.
Since ![]() and
and ![]() , then
, then ![]() , and
, and ![]()
This means that ![]() . In other words, those three triangles are similar.
. In other words, those three triangles are similar.
Since ![]() is the circumcenter of
is the circumcenter of ![]() ,
,
then ![]()
Let ![]() be the height of
be the height of ![]() to side
to side ![]()
Then, ![]() , thus
, thus ![]()
Since ![]() is the height of
is the height of ![]() to side
to side ![]() , then using similar triangles,
, then using similar triangles,
![]() . Therefore,
. Therefore, ![]() . Solving for
. Solving for ![]() we have:
we have:
![]()
By similar triangles,
![]()
Using Heron's formula,
![]() , where
, where ![]() we have:
we have:

![]()
![]() , thus
, thus ![]()
![]()
~Tomas Diaz. orders@tomasdiaz.com
Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.
See Also
| Mock AIME 3 Pre 2005 (Problems, Source) | ||
| Preceded by Problem 13 |
Followed by Problem 15 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||