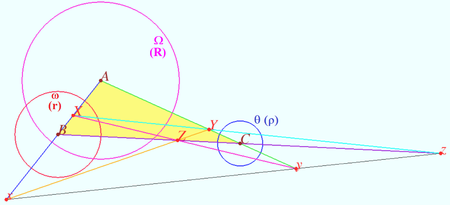
Monge's Theorem
|
|
| A diagram of Monge's theorem; |
Monge's Theorem is a theorem in Euclidean geometry.
Contents
[hide]Statement
Given three circles, ![]() and
and ![]() , none of which lies completely inside one of the others, if we construct the intersections of their common external tangents, these intersections are collinear.
, none of which lies completely inside one of the others, if we construct the intersections of their common external tangents, these intersections are collinear.
For the rest of this article, we will denote the intersections of the external tangents to ![]() and
and ![]() and
and ![]() and
and ![]() by
by ![]() respectively. Note that the external tangent to two circles is a line tangent to both of them which doesn't pass through the segment connecting the circles' centers. Exactly two of these tangents exist for any two circles not contained in each other. Internal tangents are defined similarly, but they pass through the segment joining the centers of the circles. If we replace two of the external tangent intersections with internal tangent intersections, the statement still holds. Each of the proofs below may be modified to show this. Also note that the degenerate cases with parallel tangents may need to be handled separately.
respectively. Note that the external tangent to two circles is a line tangent to both of them which doesn't pass through the segment connecting the circles' centers. Exactly two of these tangents exist for any two circles not contained in each other. Internal tangents are defined similarly, but they pass through the segment joining the centers of the circles. If we replace two of the external tangent intersections with internal tangent intersections, the statement still holds. Each of the proofs below may be modified to show this. Also note that the degenerate cases with parallel tangents may need to be handled separately.
Proof 1 (Menelaus' Theorem)
![[asy] import geometry; size(6cm); point O2 = (0, 0); point O3 = (1, 0); real r2 = 0.3; real r3 = 0.5; circle omega2 = circle(O2, r2); circle omega3 = circle(O3, r3); draw(omega2); draw(omega3); dot("$O_2$", O2, S); dot("$O_3$", O3, S); point X = O2 + (1 / (1 - r3 / r2)) * (O3 - O2); line[] t = tangents(omega2, X); draw(t, red); dot("$X$", X, S); draw(X--O3, dotted); point P = intersectionpoint(t[1], perpendicular(O2, t[1])); point Q = intersectionpoint(t[1], perpendicular(O3, t[1])); draw(O2--P, dotted); draw(O3--Q, dotted); dot("$P$", P, N); dot("$Q$", Q, N); [/asy]](http://latex.artofproblemsolving.com/0/f/9/0f930233941bb28608a96657f65be9c380f3cb0d.png)
Let ![]() be the centers and
be the centers and ![]() be the radii of
be the radii of ![]() respectively. First consider
respectively. First consider ![]() and
and ![]() .
. ![]() lies on line
lies on line ![]() . Let one of the two common tangents touch
. Let one of the two common tangents touch ![]() at
at ![]() , and touch
, and touch ![]() at
at ![]() .
. ![]() , hence
, hence ![]() As
As ![]() doesn't lie on segment
doesn't lie on segment ![]() , we get
, we get ![\[\frac{\overrightarrow{O_2X}}{\overrightarrow{XO_3}}=-\frac{r_2}{r_3}.\]](http://latex.artofproblemsolving.com/f/6/8/f681609e14196bc21a0141e4a6e3999e212b26b1.png) Similarly,
Similarly, ![\[\frac{\overrightarrow{O_3Y}}{\overrightarrow{YO_1}}=-\frac{r_3}{r_1}, \frac{\overrightarrow{O_1Z}}{\overrightarrow{ZO_2}}=-\frac{r_1}{r_2}.\]](http://latex.artofproblemsolving.com/3/b/4/3b4724e78e1d4f07ad0fd6b7d80a0cabb9ea1b6f.png) Therefore,
Therefore, ![\[\frac{\overrightarrow{O_2X}}{\overrightarrow{XO_3}}\cdot\frac{\overrightarrow{O_3Y}}{\overrightarrow{YO_1}}\cdot\frac{\overrightarrow{O_1Z}}{\overrightarrow{ZO_2}}=\left(-\frac{r_2}{r_3}\right)\left(-\frac{r_3}{r_1}\right)\left(-\frac{r_1}{r_2}\right)=-1.\]](http://latex.artofproblemsolving.com/e/8/2/e829b53edfd11cf08d136cacc1db6015b15de394.png) By Menelaus' theorem,
By Menelaus' theorem, ![]() and
and ![]() are collinear.
are collinear. ![]()
Proof 2 (Homothety)
Let ![]() be the positive homothety taking
be the positive homothety taking ![]() to
to ![]() . Let
. Let ![]() be the positive homothety taking
be the positive homothety taking ![]() to
to ![]() .
. ![]() and
and ![]() have centers
have centers ![]() and
and ![]() respectively. Consider
respectively. Consider ![]() . It is well known that the composition of two homotheties is also a homothety, with center lying on the line joining the centers of the two original homotheties. Also, its coefficient of homothety equals the product of the coefficients of the original two homotheties, so we know that the coefficient of
. It is well known that the composition of two homotheties is also a homothety, with center lying on the line joining the centers of the two original homotheties. Also, its coefficient of homothety equals the product of the coefficients of the original two homotheties, so we know that the coefficient of ![]() is positive. As
is positive. As ![]() takes
takes ![]() to
to ![]() we know its center is
we know its center is ![]() . Therefore
. Therefore ![]() are collinear.
are collinear. ![]()
This proof is particularly useful because it shows a more general claim: For any three circles, their pairwise exsimilicenters are collinear.
Proof 3 (Desargues' Theorem)
![[asy] import geometry; size(10cm); point O1 = (-0.5, 0.5); point O2 = (1.0, 1.0); point O3 = (0.3, -0.5); dot(O1); dot(O2); dot(O3); real r1 = 0.2; real r2 = 0.7; real r3 = 0.3; circle omega1 = circle(O1, r1); circle omega2 = circle(O2, r2); circle omega3 = circle(O3, r3); draw(omega1); draw(omega2); draw(omega3); point X = O2 + (1 / (1 - r3 / r2)) * (O3 - O2); point Y = O3 + (1 / (1 - r1 / r3)) * (O1 - O3); point Z = O1 + (1 / (1 - r2 / r1)) * (O2 - O1); dot("$X$", X); dot("$Y$", Y, NE); dot("$Z$", Z, SE); line[] t1 = tangents(omega3, X); line[] t2 = tangents(omega1, Y); line[] t3 = tangents(omega2, Z); draw(t1[0], red); draw(t2[0], red); draw(t3[1], red); point A1 = intersectionpoint(t2[0], t3[1]); point A2 = intersectionpoint(t3[1], t1[0]); point A3 = intersectionpoint(t1[0], t2[0]); point I = intersectionpoint(line(A1, O1), line(A2, O2)); draw(X--Y, purple + dotted); draw(X--O2, dotted); draw(Y--O3, dotted); draw(Z--O2, dotted); draw(A1--I, blue + dashed); draw(A2--I, blue + dashed); draw(A3--I, blue + dashed); dot("$A_1$", A1, N); dot("$A_2$", A2); dot("$A_3$", A3); dot("$O_1$", O1, NE); dot("$O_2$", O2, NW); dot("$O_3$", O3, E); [/asy]](http://latex.artofproblemsolving.com/9/f/9/9f9c7071122d7d0a4795aa5cfbd31b08a88e5733.png)
Let ![]() be the centers of
be the centers of ![]() respectively. Let
respectively. Let ![]() be the external tangent to
be the external tangent to ![]() which doesn't intersect
which doesn't intersect ![]() . Define
. Define ![]() and
and ![]() similarly. Let
similarly. Let ![]() be the intersection of
be the intersection of ![]() and
and ![]() . Define
. Define ![]() and
and ![]() similarly. Note that
similarly. Note that ![]() lie on
lie on ![]() respectively.
respectively.
Lines ![]() are the internal angle bisectors in
are the internal angle bisectors in ![]() hence they concur in the incenter of
hence they concur in the incenter of ![]() As
As ![]() and
and ![]() are perspective from a point, by Desargues' theorem, they are also perspective from a line, hence
are perspective from a point, by Desargues' theorem, they are also perspective from a line, hence ![]() are collinear, but these are precisely the points
are collinear, but these are precisely the points ![]()
![]()
Degenerate cases
If any two of ![]() are congruent, their external tangents are parallel. The non-projective proofs fail in these cases, so they need to be handled separately.
are congruent, their external tangents are parallel. The non-projective proofs fail in these cases, so they need to be handled separately.
If all three circles are congruent, all three tangent pairs are parallel, so ![]() are all points at infinity. Hence, all of them lie on the line at infinity.
are all points at infinity. Hence, all of them lie on the line at infinity.
If two circles are congruent (say ![]() and
and ![]() ) and the third isn't (
) and the third isn't (![]() ,) then
,) then ![]() is a point at infinity of the pencil of lines parallel to
is a point at infinity of the pencil of lines parallel to ![]() and
and ![]() and
and ![]() are Euclidean (ordinary) points. By similarity (similar to proof 1,) we get
are Euclidean (ordinary) points. By similarity (similar to proof 1,) we get ![\[\frac{\overrightarrow{O_1Y}}{\overrightarrow{O_1O_3}}=\frac{\overrightarrow{O_1Z}}{\overrightarrow{O_1O_2}},\]](http://latex.artofproblemsolving.com/7/9/0/7905d1d768f3412e81c3a9757460e8d90ffe62ab.png) hence
hence ![]() so
so ![]() are collinear.
are collinear.
Monge's Theorem for centers
Let circles ![]() centered at points
centered at points ![]() with radii
with radii ![]() be given.
be given.
In accordance with Wolfram mathworld we name insimilicenter (Internal Similitude Center) of circles ![]() and
and ![]() the point
the point ![]() and exsimilicenter (External Similitude Center) the point
and exsimilicenter (External Similitude Center) the point ![]() If neither of the two circles lies entirely inside the other, then this point is the intersection of their external tangents.
If neither of the two circles lies entirely inside the other, then this point is the intersection of their external tangents.
Similarly denote ![]() and
and ![]() as centers of pares
as centers of pares ![]() and
and ![]()
The triples of points ![]() and
and ![]() are collinear.
are collinear.
Proof
![]() so (according Menelaus' theorem) line
so (according Menelaus' theorem) line ![]() crossed sidelines of
crossed sidelines of ![]()





![[asy] import geometry; size(6cm); point O1 = (-0.5, 0.5); point O2 = (1.0, 1.0); point O3 = (0.3, -0.5); dot(O1); dot(O2); dot(O3); real r1 = 0.2; real r2 = 0.7; real r3 = 0.3; circle omega1 = circle(O1, r1); circle omega2 = circle(O2, r2); circle omega3 = circle(O3, r3); draw(omega1); draw(omega2); draw(omega3); point X = O2 + (1 / (1 - r3 / r2)) * (O3 - O2); point Y = O3 + (1 / (1 - r1 / r3)) * (O1 - O3); point Z = O1 + (1 / (1 - r2 / r1)) * (O2 - O1); dot("$X$", X); dot("$Y$", Y, NE); dot("$Z$", Z, SE); line[] t1 = tangents(omega3, X); line[] t2 = tangents(omega1, Y); line[] t3 = tangents(omega2, Z); draw(t1, red); draw(t2, red); draw(t3, red); draw(X--Y, purple + dotted); [/asy]](http://latex.artofproblemsolving.com/8/b/2/8b2c4d16bb7eeb093ee6d31793afc716ed3269ca.png)