Japanese Theorem
The Japanese theorem exists for both cyclic quadrilaterals and cyclic polygons.
Contents
[hide]Japanese theorem for cyclic quadrilaterals
Definition
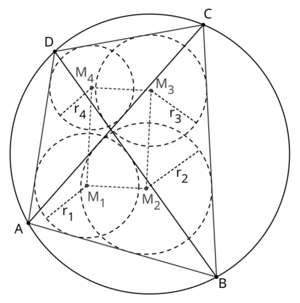
The Japanese theorem for cyclic quadrilaterals states that for a cyclic quadrilateral 
and incenters 
, 
, 
, 
of triangles 
, 
, 
, 
the quadrilateral 
is a rectangle.
Proof
From , we can see that
Similarly, from we have
Since is cyclic, therefore 
, which means that
From this, it follows that 
is cyclic. This means that
By symmetry, we can also derive
Adding these equations up, we get
Which implies
And other angles similarly.
Japanese theorem for cyclic polygons
Definition
The Japanese theorem for cyclic polygons states that for any triangulated cyclic polygon, the sum of the inradii of the triangles is constant.
