Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Symmedians, Lemoine point"

(→‎Symmedian and tangents)
(→‎Symmedian and tangents)
 
(No difference)

Latest revision as of 15:04, 9 July 2024

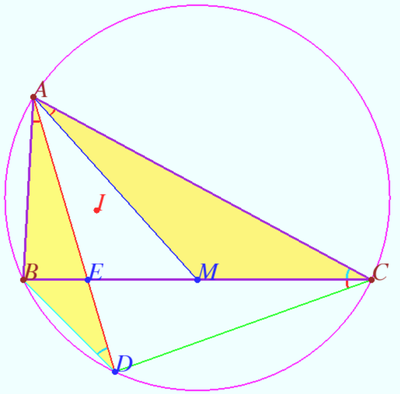
The reflecting of the median over the corresponding angle bisector is the symmedian. The angle formed by the symmedian and the angle bisector has the same measure as the angle between the median and the angle bisector, but it is on the other side of the angle bisector. The symmedian $AS_A$ is isogonally conjugate to the median $AM_A.$

There are three symmedians. They are meet at a triangle center called the Lemoine point.

Proportions

Symedian segments.png

Let $\triangle ABC$ be given.

Let $AM$ be the median, $\Omega = \odot ABC, E \in BC, D = AE \cap \Omega \ne A.$

Prove that iff $AE$ is the symmedian than $\frac {BD}{CD} = \frac{AB}{AC}, \frac {BE}{CE} = \left (\frac{AB}{AC} \right )^2.$

Proof

1. Let $AE$ be the symmedian. So $\angle BAD = \angle CAM.$ \[\angle BDA = \angle ACB = \angle ACM \implies \triangle ABD \sim \triangle AMC \implies\] \[\frac {AM}{MC}= \frac {AB}{BD}.\] Similarly $\triangle ABM \sim \triangle ADC \implies \frac {AM}{MB}= \frac {AC}{CD}.$ \[BM = MC \implies \frac {BD}{CD} = \frac{AB}{AC}.\]

By applying the Law of Sines we get \[\frac{AB}{\sin \angle AEB} = \frac{BE}{\sin \angle BAD}, \frac{CD}{\sin \angle CED} = \frac{CE}{\sin \angle CDE},\] \[\frac{AC}{\sin \angle ADC} = \frac{BD}{\sin \angle BAD} \implies \frac {BE}{CE} = \frac{AB}{CD} \cdot \frac {BD}{AC} = \frac{AB^2}{AC^2}.\] Similarly, $\frac {AE}{ED} = \frac{AB^2}{BD^2}.$

2. $\frac {BD}{CD} = \frac{AB}{AC}.$

As point $D$ moves along the fixed arc $BC$ from $B$ to $C$, the function $F(D) = \frac {BD}{CD}$ monotonically increases from zero to infinity. This means that there is exactly one point at which the condition is satisfied. In this case, point $D$ lies on the symmedian.

Similarly for point $E.$

Corollary

Let $AE$ be the $A-$ symmedian of $\triangle ABC.$

Then $BE$ is the $B-$ symmedian of $\triangle ABD, CE$ is the $C-$ symmedian of $\triangle ACD, DE$ is the $D-$ symmedian of $\triangle BCD.$

vladimir.shelomovskii@gmail.com, vvsss

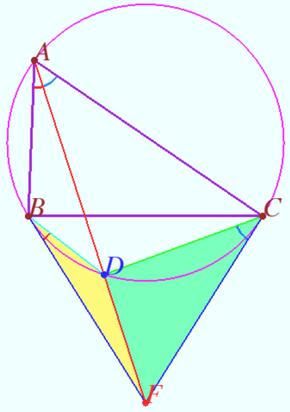
Symmedian and tangents

Tangents and symmedian.png

Let $\triangle ABC$ and it’s circumcircle $\Omega$ be given. Tangents to $\Omega$ at points $B$ and $C$ intersect at point $F.$ Prove that $AF$ is $A-$ symmedian of $\triangle ABC.$

Proof

Denote $D = AF \cap \Omega \ne A.$ WLOG, $\angle BAC < 180^\circ.$ \[\triangle FDB \sim \triangle FBA \implies \frac {BD}{AB} = \frac{DF}{BF}.\] \[\triangle FDC \sim \triangle FCA \implies \frac {CD}{AC} = \frac{DF}{CF}.\] $BF = CF \implies \frac {BD}{CD} = \frac{AB}{AC} \implies AD$ is $A-$ symmedian of $\triangle ABC.$

vladimir.shelomovskii@gmail.com, vvsss

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Symmedians,_Lemoine_point&oldid=221974"