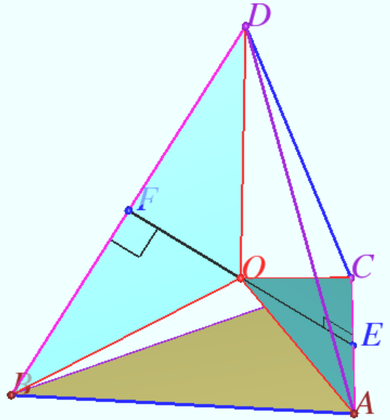
Disphenoid
Disphenoid is a tetrahedron whose four faces are congruent acute-angled triangles.
Contents
Main
a) A tetrahedron ![]() is a disphenoid iff
is a disphenoid iff ![]()
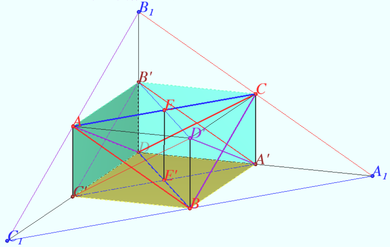
b) A tetrahedron is a disphenoid iff its circumscribed parallelepiped is right-angled.
c) Let ![]() The squares of the lengths of sides its circumscribed parallelepiped and the bimedians are:
The squares of the lengths of sides its circumscribed parallelepiped and the bimedians are:
![]()
![]() The circumscribed sphere has radius (the circumradius):
The circumscribed sphere has radius (the circumradius):
![]()
The volume of a disphenoid is:
![]() Each height of disphenoid
Each height of disphenoid ![]() is
is ![]() the inscribed sphere has radius:
the inscribed sphere has radius: ![]() where
where ![]() is the area of
is the area of ![]()
Proof
a) ![]()
![]() because in
because in ![]() there is no equal sides.
there is no equal sides.
Let consider ![]()
![]() but one of sides need be equal
but one of sides need be equal ![]() so
so ![]()
b) Any tetrahedron can be assigned a parallelepiped by drawing a plane through each edge of the tetrahedron parallel to the opposite edge.
![]() is parallelogram with equal diagonals, i.e. rectangle.
is parallelogram with equal diagonals, i.e. rectangle.
Similarly, ![]() and
and ![]() are rectangles.
are rectangles.
If ![]() is rectangle, then
is rectangle, then ![]()
Similarly, ![]() is a disphenoid.
is a disphenoid.
c) ![]()
Similarly, ![]()
![]()
Similarly, ![]()
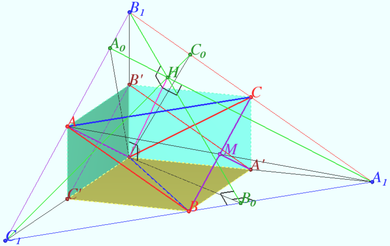
Let ![]() be the midpoint
be the midpoint ![]() ,
, ![]() be the midpoint
be the midpoint ![]()
![]() is the bimedian of
is the bimedian of ![]() and
and ![]()
![]()
The circumscribed sphere of ![]() is the circumscribed sphere of
is the circumscribed sphere of ![]() so it is
so it is
![]()
The volume of a disphenoid is third part of the volume of ![]() so:
so:
![]() The volume of a disphenoid is
The volume of a disphenoid is ![]() where
where ![]() is any height.
is any height.
The inscribed sphere has radius ![]()
![]()
![]()
![]()
![]()
Therefore ![]()
Corollary
![]() is acute-angled triangle, becouse
is acute-angled triangle, becouse ![]()
vladimir.shelomovskii@gmail.com, vvsss
Constructing
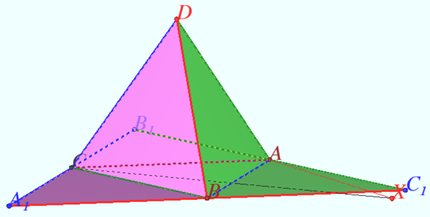
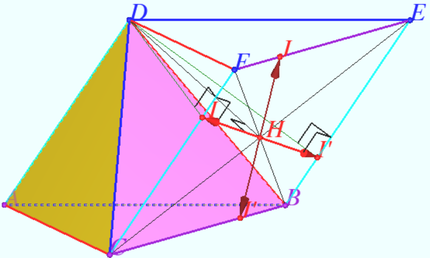
Let triangle ![]() be given. Сonstruct the disphenoid
be given. Сonstruct the disphenoid ![]()
Solution
Let ![]() be the anticomplementary triangle of
be the anticomplementary triangle of ![]() be the midpoint
be the midpoint ![]()
Then ![]() is the midpoint of segment
is the midpoint of segment ![]()
![]() is the midpoint
is the midpoint ![]()
Similarly, ![]() is the midpoint
is the midpoint ![]() is the midpoint
is the midpoint ![]()
So, ![]()
Let ![]() be the altitudes of
be the altitudes of ![]() be the orthocenter of
be the orthocenter of ![]()
To construct the disphenoid ![]() using given triangle
using given triangle ![]() we need:
we need:
1) Construct ![]() the anticomplementary triangle of
the anticomplementary triangle of ![]()
2) Find the orthocenter ![]() of
of ![]()
3) Construct the perpendicular from point ![]() to plane
to plane ![]()
4) Find the point ![]() in this perpendicular such that
in this perpendicular such that ![]()
vladimir.shelomovskii@gmail.com, vvsss
Properties and signs of disphenoid
Three sums of the plane angles
The sums of the plane angles (the angular defects) at any three vertices of the tetrahedron are equal to ![]() iff the tetrahedron is disphenoid.
iff the tetrahedron is disphenoid.
Proof
The sum of the all plane angles of the tetrahedron is the sum of plane angles of four triangles, so the sum of plane angles of fourth vertice is ![]()
The development of the tetrahedron ![]() on the plane
on the plane ![]() is a hexagon
is a hexagon ![]()
a) If the angular defect of vertex ![]() is
is ![]() then angle
then angle
![]() so points
so points ![]() and
and ![]() are collinear.
are collinear.
Similarly, triples of points ![]() and
and ![]() are collinear.
are collinear.
The hexagon ![]() is the triangle, where the points
is the triangle, where the points ![]() and
and ![]() are the midpoints of sides
are the midpoints of sides ![]() and
and ![]() respectively.
respectively.
Consequently, ![]()
Similarly, all faces of the tetrahedron are equal. The tetrahedron is disphenoid.
b) If the tetrahedron is disphenoid, then any two of its adjacent faces form a parallelogram when developed.
Consequently, the development of the tetrahedron is a triangle, i.e. the sums of the plane angles at the vertices of the tetrahedron are equal to ![]()
Angular defects at two vertices and pair of opposite edges
The tetrahedron is disphenoid if the sums of the plane angles (the angular defects) at any two vertices of the tetrahedron are equal to ![]() and any two opposite edges are equal.
and any two opposite edges are equal.
Proof
Let the sums of the plane angles at vertices ![]() and
and ![]() be equal to
be equal to ![]()
Consider the development of the tetrahedron on the plane of face ![]()
The triples of points ![]() and
and ![]() are collinear.
are collinear. ![]() lies on bisector of segment
lies on bisector of segment ![]()
Case 1. Let the edges ![]() and
and ![]() are equal.
are equal.
![]() is the midsegment
is the midsegment ![]()
![]() is the midpoint of the segment
is the midpoint of the segment ![]()
the sum of the plane angles at vertices ![]() is equal to
is equal to ![]() is disphenoid.
is disphenoid.
Case 2. The edges other than ![]() and
and ![]() are equal. WLOG,
are equal. WLOG, ![]()
![]() Note that in the process of constructing the development onto the plane
Note that in the process of constructing the development onto the plane ![]() the image of the face
the image of the face ![]() and the face
and the face ![]() are in different half-planes of the line
are in different half-planes of the line ![]()
Accordingly, the image of the vertex ![]() of the face
of the face ![]() and the vertex
and the vertex ![]() are located on different sides of the line
are located on different sides of the line ![]()
There are only two points on bisector of segment ![]() such that distance from
such that distance from ![]() is equal to
is equal to ![]()
One of them is designated as ![]() on the diagram. It lies at the same semiplane
on the diagram. It lies at the same semiplane ![]() as
as ![]() which is impossible.
which is impossible.
The second is the midpoint of segment ![]()
the sum of the plane angles at vertices ![]() is equal to
is equal to ![]() is disphenoid.
is disphenoid.
Angular defect at vertex and two pair of opposite edges
The tetrahedron is disphenoid if the sum of the plane angles (the angular defects) at one vertex of the tetrahedron is equal to ![]() and two pare of opposite edges are equal.
and two pare of opposite edges are equal.
Proof
WLOG, the sum of the plane angles at vertex ![]() is equal to
is equal to ![]()
Consider the development of the tetrahedron on the plane ![]()
![]() is a parallelogram
is a parallelogram ![]() is a parallelogram.
is a parallelogram.
Therefore, ![]() is disphenoid.
is disphenoid.
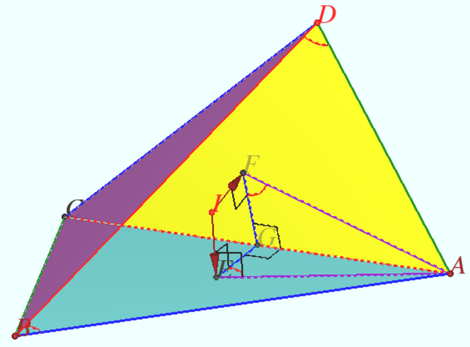
Circumcenter and incenter coinside
A tetrahedron is a disphenoid if the centers of the circumscribed sphere and the inscribed sphere coincide.
Proof
Denote ![]() the incenter - circumcenter,
the incenter - circumcenter, ![]() and
and ![]() the points of tangency of the inscribed sphere with the faces
the points of tangency of the inscribed sphere with the faces ![]() and
and ![]()
![]() is circumradius of
is circumradius of ![]() is circumradius of
is circumradius of ![]()
![]() is circumcenter of
is circumcenter of ![]() is circumradius of
is circumradius of ![]()
![]()
![]()
![]()
![]()
![]() Similarly,
Similarly, ![]()
![]() Similarly, the sums of the plane angles in vertices
Similarly, the sums of the plane angles in vertices ![]() and
and ![]() are
are ![]()
Therefore, ![]() is the disphenoid.
is the disphenoid.
Circumcenter and centroid coinside
A tetrahedron is a disphenoid if the centers of the circumscribed sphere and the centroid coincide.
Proof
Let ![]() and
and ![]() be the midpoints of the edges
be the midpoints of the edges ![]() and
and ![]()
![]() be the centroid of the tetrahedron
be the centroid of the tetrahedron ![]()
![]() is the midpoint of
is the midpoint of ![]()
The two sides and the median uniquely determine the third side, so ![]()
Similarly, ![]() is the disphenoid.
is the disphenoid.
Equal areas of faces
Prove that ![]() is a disphenoid if the areas of all faces of tetrahedron are equal.
is a disphenoid if the areas of all faces of tetrahedron are equal.
Proof
Let's complete the tetrahedron ![]() to a prism
to a prism ![]()
![]()
![]()
![]()
![]() where
where ![]() is the area of
is the area of ![]()
Let ![]() be the height of
be the height of ![]() points
points ![]() are collinear.
are collinear.
![]() Similarly,
Similarly, ![]()
![]()
![]() Similarly,
Similarly, ![]() is disphenoid.
is disphenoid.