Difference between revisions of "Mock AIME 2 2006-2007 Problems/Problem 14"
m |
|||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
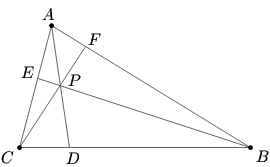
| − | In triangle ABC, <math>\displaystyle AB = 308</math> and <math>\displaystyle AC=35 | + | In [[triangle]] <math>ABC</math>, <math>\displaystyle AB = 308</math> and <math>\displaystyle AC=35</math>. Given that <math>\displaystyle AD</math>, <math>\displaystyle BE,</math> and <math>\displaystyle CF,</math> [[intersect]] at <math>\displaystyle P</math> and are an [[angle bisector]], [[median of a triangle | median]], and [[altitude]] of the triangle, respectively, compute the [[length]] of <math>\displaystyle BC.</math> |
[[Image:Mock AIME 2 2007 Problem14.jpg]] | [[Image:Mock AIME 2 2007 Problem14.jpg]] | ||
==Solution== | ==Solution== | ||
| − | {{ | + | Let <math>BC = x</math>. |
| + | |||
| + | By the [[Angle Bisector Theorem]], <math>\frac{CD}{BD} = \frac{AC}{AB} = \frac{35}{308} = \frac{5}{44}</math>. | ||
| + | |||
| + | Let <math>CF = h</math>. Then by the [[Pythagorean Theorem]], <math>h^2 + AF^2 = 35^2</math> and <math>h^2 + BF^2 = x^2</math>. Subtracting the former [[equation]] from the latter to eliminate <math>h</math>, we have <math>BF^2 - AF^2 = x^2 - 35^2</math> so <math>(BF + AF)(BF - AF) = x^2 - 1225</math>. Since <math>BF + AF = AB = 308</math>, <math>BF - AF = \frac{x^2 - 1225}{308}</math>. We can solve these equations for <math>BF</math> and <math>AF</math> in terms of <math>x</math> to find that <math>BF = 154 + \frac{x^2 - 1225}{616} = </math> and <math>AF = 154 - \frac{x^2 - 1225}{616}</math>. | ||
| + | |||
| + | Now, by [[Ceva's Theorem]], <math>\frac{AE}{EC} \cdot \frac{CD}{DB} \cdot \frac{BF}{FA} = 1</math>, so <math>1 \cdot \frac{5}{44} \cdot \frac{BF}{AF} = 1</math> and <math>5BF = 44AF</math>. Plugging in the values we previously found, | ||
| + | |||
| + | <math>5\cdot 154 + \frac{5(x^2 - 1225)}{616} = 44\cdot 154 - \frac{44(x^2 - 1225)}{616}</math> | ||
| + | |||
| + | so | ||
| + | |||
| + | <math>\frac{49}{616}(x^2 - 1225) = 39\cdot 154</math> | ||
| + | |||
| + | and | ||
| + | |||
| + | <math>x^2 - 1225 = 75504</math> | ||
| + | |||
| + | which yields finally <math>x = 277</math>. | ||
---- | ---- | ||
| Line 18: | Line 36: | ||
== Problem Source == | == Problem Source == | ||
4everwise thought of this problem after reading the first chapter of Geometry Revisited. | 4everwise thought of this problem after reading the first chapter of Geometry Revisited. | ||
| + | |||
| + | [[Category:Intermediate Geometry Problems]] | ||
Revision as of 17:15, 15 February 2007
Problem
In triangle 
, 
and 
. Given that 
, 
and 
intersect at 
and are an angle bisector, median, and altitude of the triangle, respectively, compute the length of 
Solution
Let 
.
By the Angle Bisector Theorem, 
.
Let 
. Then by the Pythagorean Theorem, 
and 
. Subtracting the former equation from the latter to eliminate 
, we have 
so 
. Since 
, 
. We can solve these equations for 
and 
in terms of 
to find that 
and 
.
Now, by Ceva's Theorem, 
, so 
and 
. Plugging in the values we previously found,
so
and
which yields finally 
.
Problem Source
4everwise thought of this problem after reading the first chapter of Geometry Revisited.
