Difference between revisions of "Two poles formula"
Jingwei325 (talk | contribs) (Created page for two pole formula/theorem because at least two pages referenced it without a link, and upon searching for it, I couldn't find it) |
Jingwei325 (talk | contribs) (→Coordinate/analytical geometry proof) |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 20: | Line 20: | ||
<cmath>ahp+bhp=abp</cmath> | <cmath>ahp+bhp=abp</cmath> | ||
<cmath>hp(a+b)=abp</cmath> | <cmath>hp(a+b)=abp</cmath> | ||
| − | |||
<cmath>h=\frac{ab}{a+b},</cmath> | <cmath>h=\frac{ab}{a+b},</cmath> | ||
as desired. | as desired. | ||
| Line 26: | Line 25: | ||
<cmath>Q.E.D.</cmath> | <cmath>Q.E.D.</cmath> | ||
<cmath>\smiley</cmath> | <cmath>\smiley</cmath> | ||
| + | |||
==Coordinate/analytical geometry proof== | ==Coordinate/analytical geometry proof== | ||
Using the same diagram as above, if we let <math>B</math> be the origin, then <math>A,C,</math> and <math>D</math> are the points <math>(0,b),(p,0)</math> and <math>(p,a),</math> respectively. Hence, <math>\overline{AC}</math> and <math>\overline{BD}</math> have slopes of <math>\frac{b-0}{0-p}=-\frac{b}{p}</math> and <math>\frac{a-0}{p-0}=\frac{a}{p}</math>, respectively, and y-intercepts of <math>(0,b)</math> and <math>(0,0)</math>, respectively. That means their equations are <math>y=-\frac{b}{p}x+b</math> and <math>y=\frac{a}{p}x</math>, respectively. | Using the same diagram as above, if we let <math>B</math> be the origin, then <math>A,C,</math> and <math>D</math> are the points <math>(0,b),(p,0)</math> and <math>(p,a),</math> respectively. Hence, <math>\overline{AC}</math> and <math>\overline{BD}</math> have slopes of <math>\frac{b-0}{0-p}=-\frac{b}{p}</math> and <math>\frac{a-0}{p-0}=\frac{a}{p}</math>, respectively, and y-intercepts of <math>(0,b)</math> and <math>(0,0)</math>, respectively. That means their equations are <math>y=-\frac{b}{p}x+b</math> and <math>y=\frac{a}{p}x</math>, respectively. | ||
| Line 34: | Line 34: | ||
<cmath>x=\frac{b}{\frac{a+b}{p}}</cmath> | <cmath>x=\frac{b}{\frac{a+b}{p}}</cmath> | ||
<cmath>x=\frac{bp}{a+b}.</cmath> | <cmath>x=\frac{bp}{a+b}.</cmath> | ||
| − | To find the ordinate, we plug in this to either equation: | + | To find the ordinate, we plug in this to either equation of <math>\overline{AC}</math> or <math>\overline{BD}</math>(in this case, we choose <math>\overline{BD}</math>'s equation because it contains fewer terms): |
<cmath>y=\frac{a}{p}x=\frac{a}{p} \cdot \frac{bp}{a+b}</cmath> | <cmath>y=\frac{a}{p}x=\frac{a}{p} \cdot \frac{bp}{a+b}</cmath> | ||
<cmath>y=\frac{abp}{p(a+b)}</cmath> | <cmath>y=\frac{abp}{p(a+b)}</cmath> | ||
| Line 41: | Line 41: | ||
<cmath>Q.E.D.</cmath> | <cmath>Q.E.D.</cmath> | ||
<cmath>\smiley</cmath> | <cmath>\smiley</cmath> | ||
| + | |||
==Image Credit== | ==Image Credit== | ||
https://images.app.goo.gl/237wxi3A4qAEWNFW8 | https://images.app.goo.gl/237wxi3A4qAEWNFW8 | ||
Revision as of 18:31, 17 August 2021
Contents
[hide]Theorem
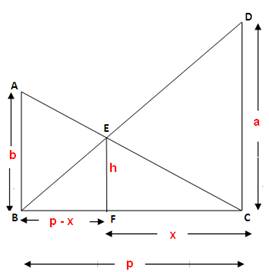
The two pole formula/theorem states that for two poles some distance apart, the height of the intersection point of the lines joining the top of either pole to the foot of the opposite pole is half the harmonic mean of the heights of the two poles(and that this is true regardless of the distance between the two poles).
Proof using similar triangles
We are looking to show that for the two poles ![]() and
and ![]() of heights
of heights ![]() and
and ![]() , respectively, and
, respectively, and ![]() units apart,
units apart, ![]() .
.
Because ![]() ,
,
![]()
![]() Because
Because ![]() ,
,
![]()
![]()
![]() Therefore,
Therefore,
![]()
![]()
![]()
![]()
![]() as desired.
as desired.
![]()
![]()
Coordinate/analytical geometry proof
Using the same diagram as above, if we let ![]() be the origin, then
be the origin, then ![]() and
and ![]() are the points
are the points ![]() and
and ![]() respectively. Hence,
respectively. Hence, ![]() and
and ![]() have slopes of
have slopes of ![]() and
and ![]() , respectively, and y-intercepts of
, respectively, and y-intercepts of ![]() and
and ![]() , respectively. That means their equations are
, respectively. That means their equations are ![]() and
and ![]() , respectively.
Setting the two equations equal to find the intersection point(recall that a point is shared by two lines if and only if it satisfies the equation of both lines), we obtain
, respectively.
Setting the two equations equal to find the intersection point(recall that a point is shared by two lines if and only if it satisfies the equation of both lines), we obtain
![]()
![]()
![]()
![]()
![]() To find the ordinate, we plug in this to either equation of
To find the ordinate, we plug in this to either equation of ![]() or
or ![]() (in this case, we choose
(in this case, we choose ![]() 's equation because it contains fewer terms):
's equation because it contains fewer terms):
![]()
![]()
![]() so
so ![]() is the ordered pair
is the ordered pair ![]() . Therefore, the height is
. Therefore, the height is ![]() , as desired.
, as desired.
![]()
![]()