Difference between revisions of "2021 Fall AMC 10B Problems/Problem 15"
(Another way to prove that CR=9) |
Ivyshine13 (talk | contribs) m (→Solution 1) |
||
| Line 26: | Line 26: | ||
Note that <math>\triangle APB \cong \triangle BQC.</math> Then, it follows that <math>\overline{PB} \cong \overline{QC}.</math> Thus, <math>QC = PB = PR + RB = 7 + 6 = 13.</math> Define <math>x</math> to be the length of side <math>CR,</math> then <math>RQ = 13-x.</math> Because <math>\overline{BR}</math> is the altitude of the triangle, we can use the property that <math>QR \cdot RC = BR^2.</math> Substituting the given lengths, we have <cmath>(13-x) \cdot x = 36.</cmath> Solving, gives <math>x = 4</math> and <math>x = 9.</math> We eliminate the possibilty of <math>x=4</math> because <math>RC > QR.</math> Thus, the side length of the square, by Pythagorean Theorem, is <cmath>\sqrt{9^2 +6^2} = \sqrt{81+36} = \sqrt{117}.</cmath> Thus, the area of the sqaure is <math>(\sqrt{117})^2 = 117,</math> so the answer is <math>\boxed{\textbf{(D) }117}.</math> | Note that <math>\triangle APB \cong \triangle BQC.</math> Then, it follows that <math>\overline{PB} \cong \overline{QC}.</math> Thus, <math>QC = PB = PR + RB = 7 + 6 = 13.</math> Define <math>x</math> to be the length of side <math>CR,</math> then <math>RQ = 13-x.</math> Because <math>\overline{BR}</math> is the altitude of the triangle, we can use the property that <math>QR \cdot RC = BR^2.</math> Substituting the given lengths, we have <cmath>(13-x) \cdot x = 36.</cmath> Solving, gives <math>x = 4</math> and <math>x = 9.</math> We eliminate the possibilty of <math>x=4</math> because <math>RC > QR.</math> Thus, the side length of the square, by Pythagorean Theorem, is <cmath>\sqrt{9^2 +6^2} = \sqrt{81+36} = \sqrt{117}.</cmath> Thus, the area of the sqaure is <math>(\sqrt{117})^2 = 117,</math> so the answer is <math>\boxed{\textbf{(D) }117}.</math> | ||
| − | Note that there is another way to prove that <math>CR = 4</math> is impossible. If <math>CR = 4,</math> then the side length would be <math>\sqrt{4^2 + 6^2} = \sqrt{52},</math> and the area would be <math>52,</math> but that isn't | + | Note that there is another way to prove that <math>CR = 4</math> is impossible. If <math>CR = 4,</math> then the side length would be <math>\sqrt{4^2 + 6^2} = \sqrt{52},</math> and the area would be <math>52,</math> but that isn't in the answer choices. Thus, <math>CR</math> must be <math>9.</math> |
~NH14 ~sl_hc | ~NH14 ~sl_hc | ||
Revision as of 11:16, 27 July 2022
Contents
[hide]Problem
In square ![]() , points
, points ![]() and
and ![]() lie on
lie on ![]() and
and ![]() , respectively. Segments
, respectively. Segments ![]() and
and ![]() intersect at right angles at
intersect at right angles at ![]() , with
, with ![]() and
and ![]() . What is the area of the square?
. What is the area of the square?
![[asy] size(170); defaultpen(linewidth(0.6)+fontsize(10)); real r = 3.5; pair A = origin, B = (5,0), C = (5,5), D = (0,5), P = (0,r), Q = (5-r,0), R = intersectionpoint(B--P,C--Q); draw(A--B--C--D--A^^B--P^^C--Q^^rightanglemark(P,R,C,7)); dot("$A$",A,S); dot("$B$",B,S); dot("$C$",C,N); dot("$D$",D,N); dot("$Q$",Q,S); dot("$P$",P,W); dot("$R$",R,1.3*S); label("$7$",(P+R)/2,NE); label("$6$",(R+B)/2,NE); [/asy]](http://latex.artofproblemsolving.com/9/3/0/9303b2a7f1e03de801c7915e1a61d7b755a6a43d.png)
![]()
Solution 1
Note that ![]() Then, it follows that
Then, it follows that ![]() Thus,
Thus, ![]() Define
Define ![]() to be the length of side
to be the length of side ![]() then
then ![]() Because
Because ![]() is the altitude of the triangle, we can use the property that
is the altitude of the triangle, we can use the property that ![]() Substituting the given lengths, we have
Substituting the given lengths, we have ![]() Solving, gives
Solving, gives ![]() and
and ![]() We eliminate the possibilty of
We eliminate the possibilty of ![]() because
because ![]() Thus, the side length of the square, by Pythagorean Theorem, is
Thus, the side length of the square, by Pythagorean Theorem, is ![]() Thus, the area of the sqaure is
Thus, the area of the sqaure is ![]() so the answer is
so the answer is ![]()
Note that there is another way to prove that ![]() is impossible. If
is impossible. If ![]() then the side length would be
then the side length would be ![]() and the area would be
and the area would be ![]() but that isn't in the answer choices. Thus,
but that isn't in the answer choices. Thus, ![]() must be
must be ![]()
~NH14 ~sl_hc
Solution 2 (Similarity, Pythagorean Theorem, and Systems of Equations
As above, note that ![]() , which means that
, which means that ![]() . In addition, note that
. In addition, note that ![]() is the altitude of a right triangle to its hypotenuse, so
is the altitude of a right triangle to its hypotenuse, so ![]() . Let the side length of the square be
. Let the side length of the square be ![]() ; using similarity side ratios of
; using similarity side ratios of ![]() to
to ![]() , we get
, we get ![]() Note that
Note that ![]() by the Pythagorean theorem, so we can use the expansion
by the Pythagorean theorem, so we can use the expansion ![]() to produce two equations and two variables;
to produce two equations and two variables;
![]()
![]()
We want ![]() , so we want to find
, so we want to find ![]() . Subtracting the first equation from the second, we get
. Subtracting the first equation from the second, we get ![]()
Then ![]() =
= ![]()
~KingRavi
Solution 3
We have that ![]() Thus,
Thus, ![]() . Now, let the side length of the square be
. Now, let the side length of the square be ![]() Then, by the Pythagorean theorem,
Then, by the Pythagorean theorem, ![]() Plugging all of this information in, we get
Plugging all of this information in, we get ![]() Simplifying gives
Simplifying gives ![]() Squaring both sides gives
Squaring both sides gives ![]() We now set
We now set ![]() and get the equation
and get the equation ![]() From here, notice we want to solve for
From here, notice we want to solve for ![]() , as it is precisely
, as it is precisely ![]() or the area of the square. So we use the Quadratic formula, and though it may seem bashy, we hope for a nice cancellation of terms.
or the area of the square. So we use the Quadratic formula, and though it may seem bashy, we hope for a nice cancellation of terms. ![]() It seems scary, but factoring
It seems scary, but factoring ![]() from the square root gives us
from the square root gives us ![]() giving us the solutions
giving us the solutions ![]() We instantly see that
We instantly see that ![]() is way too small to be an area of this square (
is way too small to be an area of this square (![]() isn't even an answer choice, so you can skip this step if out of time) because then the side length would be
isn't even an answer choice, so you can skip this step if out of time) because then the side length would be ![]() and then, even the largest line you can draw inside the square (the diagonal) is
and then, even the largest line you can draw inside the square (the diagonal) is ![]() which is less than
which is less than ![]() (line
(line ![]() ) And thus,
) And thus, ![]() must be
must be ![]() , and our answer is
, and our answer is ![]()
![]()
~wamofan
Solution 4 (Point-line distance formula)
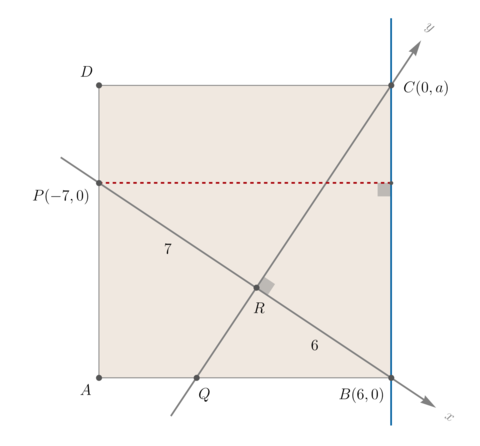
Denote ![]() . Now tilt your head to the right and view
. Now tilt your head to the right and view ![]() and
and ![]() as the origin,
as the origin, ![]() -axis and
-axis and ![]() -axis, respectively. In particular, we have points
-axis, respectively. In particular, we have points ![]() . Note that side length of the square
. Note that side length of the square ![]() is
is ![]() . Also equation of line
. Also equation of line ![]() is
is
![\[\underbrace{\frac{x}{6} + \frac{y}{a} = 1}_{\text{intercepts form}} \quad \implies \quad ax + 6y - 6a = 0.\]](http://latex.artofproblemsolving.com/b/c/b/bcb9e70d5414a5c7f81392273aee5aa26b65f0dc.png) Because the distance from
Because the distance from ![]() to line
to line ![]() is also the side length
is also the side length ![]() , we can apply the point-line distance formula to get
, we can apply the point-line distance formula to get
![]() which reduces to
which reduces to ![]() . Since
. Since ![]() is positive, the last equations factors as
is positive, the last equations factors as
![]() . Now judging from the figure, we learn that
. Now judging from the figure, we learn that ![]() . So
. So ![]() .
Therefore, the area of the square
.
Therefore, the area of the square ![]() is
is ![]() . Choose
. Choose ![]() .
. ![]()
~VensL.
Solution 5
Denote ![]() .
Because
.
Because ![]() ,
, ![]() .
.
Hence, ![]() ,
, ![]() .
.
Because ![]() is a square,
is a square, ![]() .
Hence,
.
Hence, ![]() .
.
Therefore,

Thus, ![]() .
.
![]() :
: ![]() .
.
Thus, ![]() .
.
Hence, ![]() .
.
Therefore, ![]() .
.
![]() :
: ![]() .
.
Thus, ![]() .
.
Hence, ![]() .
.
However, we observe ![]() .
Therefore, in this case, point
.
Therefore, in this case, point ![]() is not on the segment
is not on the segment ![]() .
.
Therefore, this case is infeasible.
Putting all cases together, the answer is ![]() .
.
~Steven Chen (www.professorchenedu.com)
Solution 6 (Answer choices and areas)
Note that if we connect points ![]() and
and ![]() , we get a triangle with height
, we get a triangle with height ![]() and length
and length ![]() . This triangle has an area of
. This triangle has an area of ![]() the square. We can now use answer choices to our advantage!
the square. We can now use answer choices to our advantage!
Answer choice A: If ![]() was
was ![]() ,
, ![]() would be
would be ![]() . The triangle would therefore have an area of
. The triangle would therefore have an area of ![]() which is not half of the area of the square. Therefore, A is wrong.
which is not half of the area of the square. Therefore, A is wrong.
Answer choice B: If ![]() was
was ![]() ,
, ![]() would be
would be ![]() . This is obviously wrong.
. This is obviously wrong.
Answer choice C: If ![]() was
was ![]() , we would have that
, we would have that ![]() is
is ![]() . The area of the triangle would be
. The area of the triangle would be ![]() , which is not half the area of the square. Therefore, C is wrong.
, which is not half the area of the square. Therefore, C is wrong.
Answer choice D: If ![]() was
was ![]() , that would mean that
, that would mean that ![]() is
is ![]() . The area of the triangle would therefore be
. The area of the triangle would therefore be ![]() which IS half the area of the square. Therefore, our answer is
which IS half the area of the square. Therefore, our answer is ![]() .
.
~Arcticturn
Video Solution by Interstigation
https://www.youtube.com/watch?v=sKC0Yt6sPi0
See Also
| 2021 Fall AMC 10B (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Problem 16 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.