Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Kimberling’s point X(24)"
Line 1: Line 1:
−
<i><b> Kimberling point X(24) </b></i>
+
== Kimberling's point X(24) ==
 
[[File:2016 USAMO 3g.png|450px|right]]
 
[[File:2016 USAMO 3g.png|450px|right]]
  
−
Perspector of Triangle <math>ABC</math> and Orthic Triangle of the Orthic Triangle.
+
Kimberling defined point X(24) as perspector of <math>\triangle ABC</math> and Orthic Triangle of the Orthic Triangle of <math>\triangle ABC</math>.
 +
 
 
<i><b>Theorem 1</b></i>
 
<i><b>Theorem 1</b></i>
 +
 
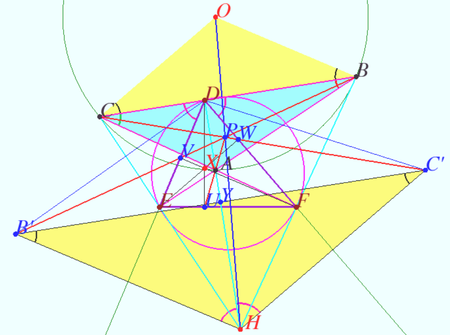
Denote <math>T_0</math> obtuse or acute <math>\triangle ABC.</math> Let <math>T_0</math> be the base triangle, <math>T_1 = \triangle DEF</math> be Orthic triangle of <math>T_0, T_2 = \triangle UVW</math> be Orthic Triangle of the Orthic Triangle of <math>T_0</math>. Let <math>O</math> and <math>H</math> be the circumcenter and orthocenter of <math>T_0.</math>  
 
Denote <math>T_0</math> obtuse or acute <math>\triangle ABC.</math> Let <math>T_0</math> be the base triangle, <math>T_1 = \triangle DEF</math> be Orthic triangle of <math>T_0, T_2 = \triangle UVW</math> be Orthic Triangle of the Orthic Triangle of <math>T_0</math>. Let <math>O</math> and <math>H</math> be the circumcenter and orthocenter of <math>T_0.</math>  
  
Line 50: Line 52:
 
Well known that <math>AH</math> is the polar of point <math>Q,</math> so <math>QO \cdot HO = QP^2 \implies QB \cdot QC = (QO – R) \cdot (QO + R) = QP^2</math>  <cmath>\implies P \in \Theta,  \Omega \perp \omega.</cmath>
 
Well known that <math>AH</math> is the polar of point <math>Q,</math> so <math>QO \cdot HO = QP^2 \implies QB \cdot QC = (QO – R) \cdot (QO + R) = QP^2</math>  <cmath>\implies P \in \Theta,  \Omega \perp \omega.</cmath>
  
−
Let <math>I_{\Omega}</math> be inversion with respect <math>\Omega, I_{\Omega}(B) = C.</math>
+
Let <math>I_{\Omega}</math> be inversion with respect <math>\Omega, I_{\Omega}(B) = C,  I_{\Omega}(H) = O.</math>
  
 
Denote <math>I_{\Omega}(D) = D',  I_{\Omega}(S) = S',</math>  
 
Denote <math>I_{\Omega}(D) = D',  I_{\Omega}(S) = S',</math>  
−
<math>QH \cdot QO = QP^2 \implies I_{\Omega}(H) = O.</math>
 
−
<math>HS \perp DD' \implies S'O \perp BC \implies BS' = CS' \implies \angle OCS' = \angle OBS'.</math>
 
−
 
−
<math>\angle QSB = \angle QCS' = \angle OCS' = \angle OBS' = \angle CSS'.</math>
 
  
−
<math>\angle BSH = 90 ^\circ  – \angle QSB = 90 ^\circ  – \angle CSS' =\angle CSH.</math>
+
<cmath>HS \perp DD' \implies S'O \perp BC \implies BS' = CS' \implies \angle OCS' = \angle OBS'.</cmath>
 +
<cmath>\angle QSB = \angle QCS' = \angle OCS' = \angle OBS' = \angle CSS'.</cmath>
 +
<cmath>\angle BSH = 90 ^\circ  – \angle QSB = 90 ^\circ  – \angle CSS' =\angle CSH.</cmath>
  
 
<i><b>Theorem 2</b></i>
 
<i><b>Theorem 2</b></i>

Revision as of 12:47, 12 October 2022

Kimberling's point X(24)

2016 USAMO 3g.png

Kimberling defined point X(24) as perspector of $\triangle ABC$ and Orthic Triangle of the Orthic Triangle of $\triangle ABC$.

Theorem 1

Denote $T_0$ obtuse or acute $\triangle ABC.$ Let $T_0$ be the base triangle, $T_1 = \triangle DEF$ be Orthic triangle of $T_0, T_2 = \triangle UVW$ be Orthic Triangle of the Orthic Triangle of $T_0$. Let $O$ and $H$ be the circumcenter and orthocenter of $T_0.$

Then $\triangle T_0$ and $\triangle T_2$ are homothetic, the point $P,$ center of this homothety lies on Euler line $OH$ of $T_0.$

The ratio of the homothety is $k = \frac {\vec {PH}}{\vec {OP}}= 4 \cos A \cos B \cos C.$

Proof

WLOG, we use case $\angle A = \alpha > 90^\circ.$ Let $B'$ be reflection $H$ in $DE.$

In accordance with Claim, $\angle BVD = \angle HVE \implies B', V,$ and $B$ are collinear.

Similarly, $C, W,$ and $C',$ were $C'$ is reflection $H$ in $DF,$ are collinear.

Denote $\angle ABC = \beta = \angle CHD, \angle ACB = \gamma = \angle BHD \implies$

$\angle HDF = \angle HDE = \angle DHB' = \angle DHC' = 180^\circ - \alpha.$

$B'C' \perp HD, BC \perp HD \implies BC|| B'C'.$ $OB = OC, HB' = HC', \angle BOC = \angle B'HC' = 360^\circ - 2 \alpha \implies OB ||HB', OC || HC' \implies$

$\triangle HB'C' \sim \triangle OBC, BB', CC'$ and $HO$ are concurrent at point $P.$

In accordance with Claim, $\angle HUF = \angle AUF \implies$ points $H$ and $P$ are isogonal conjugate with respect $\triangle UVW.$

$\angle HDE = \alpha - 90^\circ, \angle HCD = 90^\circ - \beta \implies$

$HB' = 2 HD \sin (\alpha - 90^\circ) = - 2 CD \tan(90^\circ- \beta) \cos \alpha = - 2 AC \cos \gamma \frac {\cos \beta}{\sin \beta} \cos \alpha = - 4 OB \cos A \cos B \cos C.$ $k = \frac {HB'}{OB} = \frac {HP}{OP}= - 4 \cos A \cos B \cos C \implies \frac {\vec {PH}}{\vec {OP}}= 4 \cos A \cos B \cos C.$

Claim

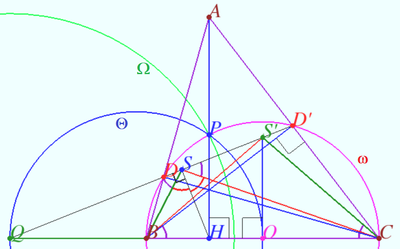
2016 3 Lemma.png

Let $\triangle ABC$ be an acute triangle, and let $AH, BD',$ and $CD$ denote its altitudes. Lines $DD'$ and $BC$ meet at $Q, HS \perp DD'.$ Prove that $\angle BSH = \angle CSH.$

Proof

Let $\omega$ be the circle $BCD'D$ centered at $O (O$ is midpoint $BC).$

Let $\omega$ meet $AH$ at $P.$ Let $\Omega$ be the circle centered at $Q$ with radius $QP.$

Let $\Theta$ be the circle with diameter $OQ.$

Well known that $AH$ is the polar of point $Q,$ so $QO \cdot HO = QP^2 \implies QB \cdot QC = (QO – R) \cdot (QO + R) = QP^2$ \[\implies P \in \Theta, \Omega \perp \omega.\]

Let $I_{\Omega}$ be inversion with respect $\Omega, I_{\Omega}(B) = C, I_{\Omega}(H) = O.$

Denote $I_{\Omega}(D) = D', I_{\Omega}(S) = S',$

\[HS \perp DD' \implies S'O \perp BC \implies BS' = CS' \implies \angle OCS' = \angle OBS'.\] \[\angle QSB = \angle QCS' = \angle OCS' = \angle OBS' = \angle CSS'.\] \[\angle BSH = 90 ^\circ – \angle QSB = 90 ^\circ – \angle CSS' =\angle CSH.\]

Theorem 2

Let $T_0 = \triangle ABC$ be the base triangle, $T_1 = \triangle DEF$ be orthic triangle of $T_0, T_2 = \triangle KLM$ be Kosnita triangle. Then $\triangle T_1$ and $\triangle T_2$ are homothetic, the point $P,$ center of this homothety lies on Euler line of $T_0,$ the ratio of the homothety is $k = \frac {\vec PH}{\vec OP} = 4 \cos A \cos B \cos C.$ We recall that vertex of Kosnita triangle are: $K$ is the circumcenter of $\triangle OBC, L$ is the circumcenter of $\triangle OAB, M$ is the circumcenter of $\triangle OAC,$ where $O$ is circumcenter of $T_0.$

vladimir.shelomovskii@gmail.com, vvsss

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Kimberling’s_point_X(24)&oldid=179061"