Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Complete Quadrilateral"

(→‎Radical axis)
(→‎Radical axis)
Line 29: Line 29:
 
Therefore power of point <math>H (H_A)</math> with respect these three circles is the same. These points lies on the common radical axis of <math>\omega, \theta,</math> and <math>\Omega \implies</math> Steiner line <math>HH_A</math> is the radical axis as desired.
 
Therefore power of point <math>H (H_A)</math> with respect these three circles is the same. These points lies on the common radical axis of <math>\omega, \theta,</math> and <math>\Omega \implies</math> Steiner line <math>HH_A</math> is the radical axis as desired.
  
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
 +
==Newton–Gauss line==
 +
[[File:Complete perpendicular.png|500px|right]]
 +
Let four lines made four triangles of a complete quadrilateral. In the diagram these are <math>\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.</math>
 +
Let points <math>K, L,</math> and <math>N</math> be the midpoints of <math>BE, CD,</math> and <math>AF,</math> respectively.
 +
Let points <math>H</math> and <math>H_A</math> be the orthocenters of <math>\triangle ABC</math> and <math>\triangle ADE,</math> respectively.
 +
Prove that Steiner line <math>HH_A</math> is perpendicular to Gauss line <math>KLN.</math>
 +
 +
<i><b>Proof</b></i>
 +
 +
Points <math>K, L,</math> and <math>N</math> are the centers of circles with diameters  <math>CD, BE,</math> and <math>AF,</math> respectively.  Steiner line <math>HH_A</math> is the radical axis of these circles.
 +
Therefore <math>HH_A \perp KL</math> as desired.
 
'''vladimir.shelomovskii@gmail.com, vvsss'''
 
'''vladimir.shelomovskii@gmail.com, vvsss'''

Revision as of 16:15, 9 December 2022

Complete quadrilateral

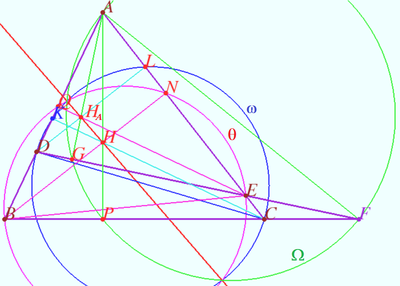
Let four lines made four triangles of a complete quadrilateral. In the diagram these are $\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.$ One can see some of the properties of this configuration and their proof using the following links.

Radical axis

Complete radical axes.png

Let four lines made four triangles of a complete quadrilateral. In the diagram these are $\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.$

Let points $H,$ and $H_A$ be the orthocenters of $\triangle ABC$ and $\triangle ADE,$ respectively.

Let circles $\omega, \theta,$ and $\Omega$ be the circles with diameters $CD, BE,$ and $AF,$ respectively. Prove that Steiner line $HH_A$ is the radical axis of $\omega, \theta,$ and $\Omega.$

Proof

Let points $G, K, L, N, P,$ and $Q$ be the foots of perpendiculars $AH_A, CH, DH_A, BH, AH,$ and $EH_A,$ respectively.

Denote $Po(X)_{\omega}$ power of point $X$ with respect the circle $\omega.$ \[\angle AGF = 90^\circ \implies G \in \Omega \implies Po(H_A)_{\Omega} = AH_A \cdot GH_A.\] \[\angle APF = 90^\circ \implies P \in \Omega \implies Po(H)_{\Omega} = AH \cdot PH_A.\] \[\angle CLD = 90^\circ \implies L \in \omega \implies Po(H_A)_{\omega} = DH_A \cdot LH_A = AH_A \cdot GH_A = Po(H_A)_{\Omega}.\] \[\angle EQB = 90^\circ \implies Q \in \theta \implies Po(H_A)_{\theta} = EH_A \cdot QH_A = AH_A \cdot GH_A = Po(H_A)_{\Omega}.\]

\[\angle BNE = 90^\circ \implies N \in \theta \implies Po(H)_{\theta} = BH \cdot NH = AH \cdot PH = Po(H)_{\Omega}.\] \[\angle CKD = 90^\circ \implies K \in \theta \implies Po(H)_{\omega} = CH \cdot KH = AH \cdot PH = Po(H)_{\Omega}.\] Therefore power of point $H (H_A)$ with respect these three circles is the same. These points lies on the common radical axis of $\omega, \theta,$ and $\Omega \implies$ Steiner line $HH_A$ is the radical axis as desired.

vladimir.shelomovskii@gmail.com, vvsss

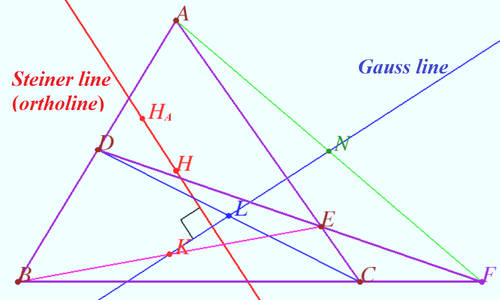
Newton–Gauss line

Complete perpendicular.png

Let four lines made four triangles of a complete quadrilateral. In the diagram these are $\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.$ Let points $K, L,$ and $N$ be the midpoints of $BE, CD,$ and $AF,$ respectively. Let points $H$ and $H_A$ be the orthocenters of $\triangle ABC$ and $\triangle ADE,$ respectively. Prove that Steiner line $HH_A$ is perpendicular to Gauss line $KLN.$

Proof

Points $K, L,$ and $N$ are the centers of circles with diameters $CD, BE,$ and $AF,$ respectively. Steiner line $HH_A$ is the radical axis of these circles. Therefore $HH_A \perp KL$ as desired. vladimir.shelomovskii@gmail.com, vvsss

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Complete_Quadrilateral&oldid=183807"