Difference between revisions of "2022 AMC 12B Problems/Problem 14"
MRENTHUSIASM (talk | contribs) (→Solution 2) |
|||
| Line 91: | Line 91: | ||
- SAHANWIJETUNGA | - SAHANWIJETUNGA | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ==Solution 6 (Complex numbers)== | ||
| + | |||
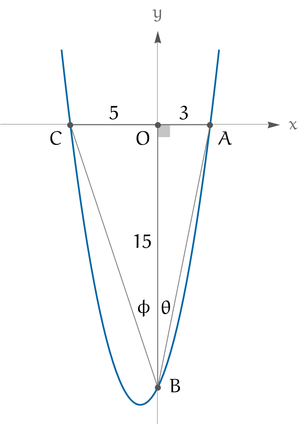
| + | [[Image:2022AMC12B14.png|center|300px]] | ||
| + | |||
| + | From <math>x^2 + 2x - 15 = (x-3)(x+5)</math>, we may assume, without loss of generality, that <math>x</math>-intercepts of the given parabola are <math>A(3,0)</math> and <math>C(-5,0)</math>. And point <math>B</math> has coordinates <math>(0,-15)</math>. Consider complex numbers <math>z = 5 + i</math> and <math>w = 3 + i</math> whose arguments are <math>\theta \coloneqq \angle OBA</math> and <math>\phi \coloneqq \angle OBC</math>, respectively. Notice that <math>\angle ABC = \theta + \phi</math> is the argument of the product <math>zw</math> which is <cmath> zw = (5+i)(3+i) = 14 + 8i. </cmath> | ||
| + | Hence <cmath>\tan \angle ABC = \frac{\operatorname{Im}(zw)}{\operatorname{Re}(zw)} = \frac{8}{14} = \boxed{\frac{4}{7}}.</cmath> | ||
| + | |||
| + | ~VensL. | ||
| + | |||
| + | |||
| + | |||
== See Also == | == See Also == | ||
{{AMC12 box|year=2022|ab=B|num-b=13|num-a=15}} | {{AMC12 box|year=2022|ab=B|num-b=13|num-a=15}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Revision as of 01:52, 10 March 2023
Contents
[hide]Problem
The graph of ![]() intersects the
intersects the ![]() -axis at points
-axis at points ![]() and
and ![]() and the
and the ![]() -axis at point
-axis at point ![]() . What is
. What is ![]() ?
?
![]()
Diagram
![[asy] /* Made by MRENTHUSIASM */ size(250); real xMin = -15; real xMax = 15; real yMin = -17; real yMax = 17; draw((xMin,0)--(xMax,0),black+linewidth(1.5),EndArrow(5)); draw((0,yMin)--(0,yMax),black+linewidth(1.5),EndArrow(5)); label("$x$",(xMax,0),(2,0)); label("$y$",(0,yMax),(0,2)); real f(real x) { return x^2+2*x-15; } draw(graph(f,-6.75,4.75),red); pair A, B, C; A = (-5,0); B = (0,-15); C = (3,0); draw(A--B--C); dot("$A$",A,1.5NW,linewidth(4.5)); dot("$B$",B,1.5SE,linewidth(4.5)); dot("$C$",C,1.5NE,linewidth(4.5)); label("$y=x^2+2x-15$",(12,9),red); [/asy]](http://latex.artofproblemsolving.com/e/1/9/e194e324298623df885f21dfe4a7f70b72af7c0a.png) ~MRENTHUSIASM
~MRENTHUSIASM
Solution 1 (Dot Product)
First, find ![]() ,
, ![]() , and
, and ![]() . Create vectors
. Create vectors ![]() and
and ![]() These can be reduced to
These can be reduced to ![]() and
and ![]() , respectively. Then, we can use the dot product to calculate the cosine of the angle (where
, respectively. Then, we can use the dot product to calculate the cosine of the angle (where ![]() ) between them:
) between them:

Thus, ![]()
~Indiiiigo
Solution 2
Note that ![]() intersects the
intersects the ![]() -axis at points
-axis at points ![]() and
and ![]() . Without loss of generality, let these points be
. Without loss of generality, let these points be ![]() and
and ![]() respectively. Also, the graph intersects the
respectively. Also, the graph intersects the ![]() -axis at point
-axis at point ![]() .
.
Let point ![]() . It follows that
. It follows that ![]() and
and ![]() are right triangles.
are right triangles.
We have ![]() Alternatively, we can use the Pythagorean Theorem to find that
Alternatively, we can use the Pythagorean Theorem to find that ![]() and
and ![]() and then use the
and then use the ![]() area formula for a triangle and the Law of Cosines to find
area formula for a triangle and the Law of Cosines to find ![]() .
.
Solution 3
Like above, we set ![]() to
to ![]() ,
, ![]() to
to ![]() , and
, and ![]() to
to ![]() , then finding via the Pythagorean Theorem that
, then finding via the Pythagorean Theorem that ![]() and
and ![]() . Using the Law of Cosines, we see that
. Using the Law of Cosines, we see that ![]() Then, we use the identity
Then, we use the identity ![]() to get
to get ![]()
~ jamesl123456
Solution 4
We can reflect the figure, but still have the same angle. This problem is the same as having points ![]() ,
, ![]() , and
, and ![]() , where we're solving for angle FED. We can use the formula for
, where we're solving for angle FED. We can use the formula for ![]() to solve now where
to solve now where ![]() is the
is the ![]() -axis to angle
-axis to angle ![]() and
and ![]() is the
is the ![]() -axis to angle
-axis to angle ![]() .
. ![]() and
and ![]() . Plugging these values into the
. Plugging these values into the ![]() formula, we get
formula, we get ![]() which is
which is ![]()
~mathboy100 (minor LaTeX edits)
Solution 5
We use the identity ![]()
Note that ![]() has side-lengths
has side-lengths ![]() and
and ![]() from Pythagorean theorem, with the area being
from Pythagorean theorem, with the area being ![]()
We equate the areas together to get: ![]() from which
from which ![]()
From Pythagorean identity, ![]()
Then we use ![]() , to obtain
, to obtain ![]()
- SAHANWIJETUNGA
Solution 6 (Complex numbers)
From ![]() , we may assume, without loss of generality, that
, we may assume, without loss of generality, that ![]() -intercepts of the given parabola are
-intercepts of the given parabola are ![]() and
and ![]() . And point
. And point ![]() has coordinates
has coordinates ![]() . Consider complex numbers
. Consider complex numbers ![]() and
and ![]() whose arguments are
whose arguments are ![]() and
and ![]() , respectively. Notice that
, respectively. Notice that ![]() is the argument of the product
is the argument of the product ![]() which is
which is ![]() Hence
Hence ![]()
~VensL.
See Also
| 2022 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 13 |
Followed by Problem 15 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()