Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Spieker center"
(→‎Incenter of medial triangle)
Line 1: Line 1:
 
The Spieker center is defined as the center of mass of the perimeter of the triangle. The Spieker center of a <math>\triangle ABC</math> is the center of gravity of a homogeneous wire frame in the shape of <math>\triangle ABC.</math> The Spieker center is a triangle center and it is listed as the point <math>X_{10}.</math>
 
The Spieker center is defined as the center of mass of the perimeter of the triangle. The Spieker center of a <math>\triangle ABC</math> is the center of gravity of a homogeneous wire frame in the shape of <math>\triangle ABC.</math> The Spieker center is a triangle center and it is listed as the point <math>X_{10}.</math>
  
−
== Incenter of medial triangle==
+
==Incenter of medial triangle==
 
[[File:Physical proof.png|400px|right]]
 
[[File:Physical proof.png|400px|right]]
−
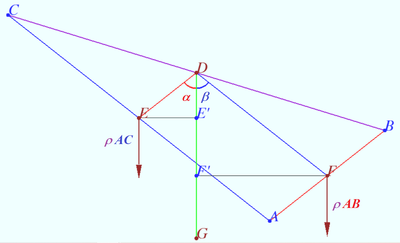
Prove that <math>X_{10}</math> is the incenter of the medial triangle <math>\triangle DEF</math> of a <math>\triangle ABC.</math>  
+
Prove that the Spieker center of triangle <math>\triangle ABC</math> is the incenter of the medial triangle <math>\triangle DEF</math> of a <math>\triangle ABC.</math>  
  
 
<i><b>Proof</b></i>
 
<i><b>Proof</b></i>
Line 20: Line 20:
  
 
This point is the incenter of the medial triangle <math>\triangle DEF.</math>  
 
This point is the incenter of the medial triangle <math>\triangle DEF.</math>  
 +
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
==Intersection of three cleavers==
 +
[[File:Cleaver.png|400px|right]]
 +
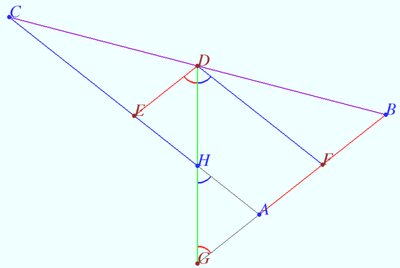
Prove that the Spieker center is located at the intersection of the three cleavers of triangle. A cleaver of a triangle is a line segment that bisects the perimeter of the triangle and has one endpoint at the midpoint of one of the three sides.
 +
 +
<i><b>Proof</b></i>
 +
 +
We use notation of previous proof. <math>DG</math> is the segment contains the Spieker center, <math>G \in AB, \angle EDG = \angle FDG, H = DG \cap AC.</math> WLOG, <math>AC > AB.</math>
 +
<cmath>DF||AC \implies \angle AHG = \angle FDG.</cmath>
 +
Similarly, <math> \angle AGH = \angle EDG =  \angle AHG \implies AH = AG \implies CH = AB + AH \implies DH</math> is cleaver.
 +
Therefore, the three cleavers meet at the Spieker center.
  
 
'''vladimir.shelomovskii@gmail.com, vvsss'''
 
'''vladimir.shelomovskii@gmail.com, vvsss'''

Revision as of 12:14, 7 August 2023

The Spieker center is defined as the center of mass of the perimeter of the triangle. The Spieker center of a $\triangle ABC$ is the center of gravity of a homogeneous wire frame in the shape of $\triangle ABC.$ The Spieker center is a triangle center and it is listed as the point $X_{10}.$

Incenter of medial triangle

Physical proof.png

Prove that the Spieker center of triangle $\triangle ABC$ is the incenter of the medial triangle $\triangle DEF$ of a $\triangle ABC.$

Proof

Let's hang up the $\triangle ABC$ in the middle of side $BC.$ Side $BC$ is balanced.

Let's replace side $AC$ with point $E$ (the center of mass of $AC,$ the midpoint $AC).$ Denote $\rho$ the linear density of a homogeneous wire frame.

The mass of point $E$ is equal to $\rho \cdot AC,$ the shoulder of the gravity force is $EE' = ED \sin \alpha = \frac {AB \sin \alpha }{2}.$

The moment of this force is $g EE' \rho \cdot AC = \frac {g \rho\cdot AC \cdot AB}{2} \sin \alpha.$

Similarly the moment gravity force acting on AB is $\frac {g \rho\cdot AC \cdot AB}{2} \sin \beta.$

Therefore, equilibrium condition is $\alpha = \beta$ and the center of gravity of a homogeneous wire frame $ABC$ lies on each bisector of $\triangle DEF.$

This point is the incenter of the medial triangle $\triangle DEF.$

vladimir.shelomovskii@gmail.com, vvsss

Intersection of three cleavers

Cleaver.png

Prove that the Spieker center is located at the intersection of the three cleavers of triangle. A cleaver of a triangle is a line segment that bisects the perimeter of the triangle and has one endpoint at the midpoint of one of the three sides.

Proof

We use notation of previous proof. $DG$ is the segment contains the Spieker center, $G \in AB, \angle EDG = \angle FDG, H = DG \cap AC.$ WLOG, $AC > AB.$ \[DF||AC \implies \angle AHG = \angle FDG.\] Similarly, $\angle AGH = \angle EDG = \angle AHG \implies AH = AG \implies CH = AB + AH \implies DH$ is cleaver. Therefore, the three cleavers meet at the Spieker center.

vladimir.shelomovskii@gmail.com, vvsss

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Spieker_center&oldid=196564"