Difference between revisions of "Spieker center"
(→Intersection of three cleavers) |
(→Intersection of three cleavers) |
||
| Line 35: | Line 35: | ||
Therefore, the three cleavers meet at the Spieker center. | Therefore, the three cleavers meet at the Spieker center. | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | ==Radical center of excircles== | ||
| + | [[File:Radical center.png|370px|right]] | ||
| + | Prove that the Spieker center of triangle is the radical center of the three excircles. | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Let <math>\triangle ABC</math> be given,<math>M_A, M_B, M_C</math> be the midpoints of <math>BC, AC, BC,</math> respectively. | ||
| + | |||
| + | Let <math>\omega_A, \omega_B, \omega_C</math> be A-excircle, B-excircle, C-excircle centered at <math>X,Y,Z,</math> respectively. | ||
| + | |||
| + | Let <math>I</math> be the incenter of <math>\triangle ABC.</math> | ||
| + | Let <math>R_A</math> be the radical axis of <math>\omega_B</math> and <math>\omega_C, R_B</math> be the radical axis of <math>\omega_A</math> and <math>\omega_C, R_C</math> be the radical axis of <math>\omega_B</math> and <math>\omega_A,</math> respectively. | ||
| + | |||
| + | It is known that the distances from <math>B</math> to the tangent points of <math>\omega_C</math> is equal to the distances from <math>C</math> to the tangent points of <math>\omega_B, BM_A = CM_A</math> therefore <math>M_A</math> lies on the radical axis <math>R_A</math> of <math>\omega_B</math> and <math>\omega_C.</math> Similarly, <math>M_B \in R_B, M_C \in R_C.</math> | ||
| + | |||
| + | <math>AI \perp ZY, R_A \perp XY \implies AI || RA \implies R_A</math> is cleaver, so the radical center of the three excircles coinside with the intersection of the three cleavers of triangle. | ||
'''vladimir.shelomovskii@gmail.com, vvsss''' | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
Revision as of 14:42, 7 August 2023
The Spieker center is defined as the center of mass of the perimeter of the triangle. The Spieker center of a ![]() is the center of gravity of a homogeneous wire frame in the shape of
is the center of gravity of a homogeneous wire frame in the shape of ![]() The Spieker center is a triangle center and it is listed as the point
The Spieker center is a triangle center and it is listed as the point ![]()
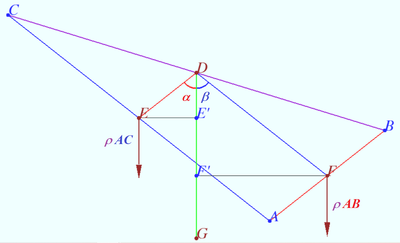
Incenter of medial triangle
Prove that the Spieker center of triangle ![]() is the incenter of the medial triangle
is the incenter of the medial triangle ![]() of a
of a ![]()
Proof
Let's hang up the ![]() in the middle of side
in the middle of side ![]() Side
Side ![]() is balanced.
is balanced.
Let's replace side ![]() with point
with point ![]() (the center of mass of
(the center of mass of ![]() the midpoint
the midpoint ![]() Denote
Denote ![]() the linear density of a homogeneous wire frame.
the linear density of a homogeneous wire frame.
The mass of point ![]() is equal to
is equal to ![]() the shoulder of the gravity force is
the shoulder of the gravity force is ![]()
The moment of this force is ![]()
Similarly the moment gravity force acting on AB is ![]()
Therefore, equilibrium condition is ![]() and the center of gravity of a homogeneous wire frame
and the center of gravity of a homogeneous wire frame ![]() lies on each bisector of
lies on each bisector of ![]()
This point is the incenter of the medial triangle ![]()
vladimir.shelomovskii@gmail.com, vvsss
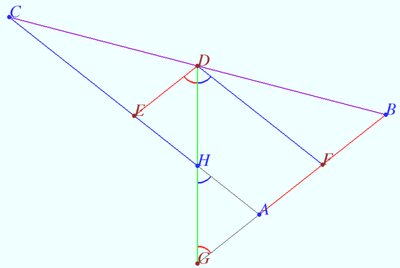
Intersection of three cleavers
Prove that the Spieker center is located at the intersection of the three cleavers of triangle. A cleaver of a triangle is a line segment that bisects the perimeter of the triangle and has one endpoint at the midpoint of one of the three sides.
Proof
We use notation of previous proof. ![]() is the segment contains the Spieker center,
is the segment contains the Spieker center, ![]() WLOG,
WLOG, ![]()
![]() Similarly,
Similarly, ![]()
So ![]() is cleaver.
is cleaver.
Therefore, the three cleavers meet at the Spieker center.
vladimir.shelomovskii@gmail.com, vvsss
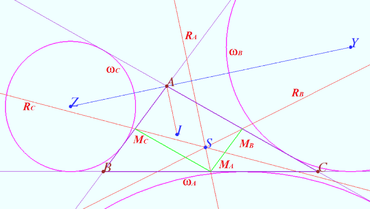
Radical center of excircles
Prove that the Spieker center of triangle is the radical center of the three excircles.
Proof
Let ![]() be given,
be given,![]() be the midpoints of
be the midpoints of ![]() respectively.
respectively.
Let ![]() be A-excircle, B-excircle, C-excircle centered at
be A-excircle, B-excircle, C-excircle centered at ![]() respectively.
respectively.
Let ![]() be the incenter of
be the incenter of ![]() Let
Let ![]() be the radical axis of
be the radical axis of ![]() and
and ![]() be the radical axis of
be the radical axis of ![]() and
and ![]() be the radical axis of
be the radical axis of ![]() and
and ![]() respectively.
respectively.
It is known that the distances from ![]() to the tangent points of
to the tangent points of ![]() is equal to the distances from
is equal to the distances from ![]() to the tangent points of
to the tangent points of ![]() therefore
therefore ![]() lies on the radical axis
lies on the radical axis ![]() of
of ![]() and
and ![]() Similarly,
Similarly, ![]()
![]() is cleaver, so the radical center of the three excircles coinside with the intersection of the three cleavers of triangle.
is cleaver, so the radical center of the three excircles coinside with the intersection of the three cleavers of triangle.
vladimir.shelomovskii@gmail.com, vvsss