Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Spieker center"

(→‎Radical center of excircles)
(→‎Nagel line)
Line 60: Line 60:
 
[[File:Nagel line.png|400px|right]]
 
[[File:Nagel line.png|400px|right]]
 
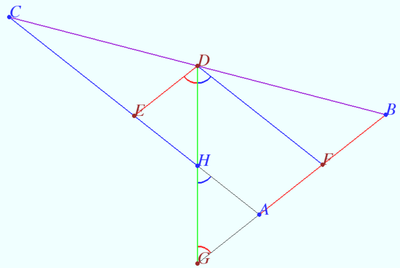
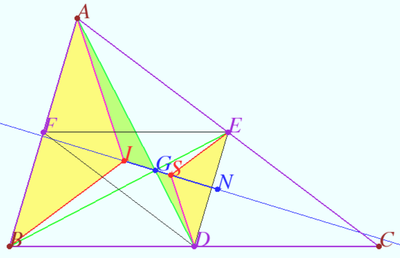
Let points <math>I, G, S</math>  be the incenter, the centroid and the  Spieker center of triangle <math>\triangle ABC,</math> respectively. Prove that points <math>I, G, S</math> are collinear, <math>IG = 2 GS,</math> and the barycentric coordinates of S are  <math>{ b+c : c+a : a+b.}</math>
 
Let points <math>I, G, S</math>  be the incenter, the centroid and the  Spieker center of triangle <math>\triangle ABC,</math> respectively. Prove that points <math>I, G, S</math> are collinear, <math>IG = 2 GS,</math> and the barycentric coordinates of S are  <math>{ b+c : c+a : a+b.}</math>
 +
 
The Nagel line is the line on which points <math>I, G, S,</math> and Nagel point <math>N</math> lie.
 
The Nagel line is the line on which points <math>I, G, S,</math> and Nagel point <math>N</math> lie.
 
   
 
   
Line 65: Line 66:
  
 
Let <math>D, E, F</math> be the midpoints of <math>BC, AC, BC,</math> respectively.
 
Let <math>D, E, F</math> be the midpoints of <math>BC, AC, BC,</math> respectively.
−
Bisector <math>AI</math> is parallel to cleaver <math>DS, BI || ES, AB ||ED, \frac {AB}{DE} = 2 \implies \triangle ABI \sim \triangle DES \implies \frac {AI}{DS} = 2.</math>
+
Bisector <math>AI</math> is parallel to cleaver <math>DS, BI || ES.</math>
−
Centroid <math>G</math> divide the median <math>AD</math> such that <math>\frac {AG}{DG} = 2 \implies \triangle AGI \sim \triangle DGS \implies \frac {GI}{SG} = 2,</math> and points <math>I, G, S</math> are collinear.
+
<cmath>AB ||ED, \frac {AB}{DE} = 2 \implies \triangle ABI \sim \triangle DES \implies \frac {AI}{DS} = 2.</cmath>
−
The barycentric coordinates of <math>I</math> are <math>{a : b : c}.</math>
+
Centroid <math>G</math> divide the median <math>AD</math> such that <math>\frac {AG}{DG} = 2 \implies </math>
−
The barycentric coordinates of <math>G</math> are <math>{1 : 1 : 1}.</math>
+
 
−
<math>GI = 2 SG \implies \vec {G} - \vec {I} = 2(\vec {S} - \vec {G}) \implies \vec {G} = \frac {3 \vec {G} - \vec {I} }{2} = {1 - \frac{a}{a+ b+c} : 1 - \frac {b}{a+b+c} : 1 - \frac{c}{a+b+c}} = { b+c : c+a : a+b.}</math>
+
<math>\triangle AGI \sim \triangle DGS \implies \frac {GI}{SG} = 2,</math> and points <math>I, G, S</math> are collinear.
 +
 
 +
The barycentric coordinates of <math>I</math> are <math>{a : b : c}.</math> The barycentric coordinates of <math>G</math> are <math>{1 : 1 : 1}.</math>
 +
 
 +
<cmath>\vec {GI} = 2 \vec {SG} \implies \vec {G} - \vec {I} = 2(\vec {S} - \vec {G}) \implies</cmath>
 +
<cmath>\vec {G} = \frac {3 \vec {G} - \vec {I} }{2} = {1 - \frac{a}{a+ b+c} : 1 - \frac {b}{a+b+c} : 1 - \frac{c}{a+b+c}} = { b+c : c+a : a+b.}</cmath>
  
 
'''vladimir.shelomovskii@gmail.com, vvsss'''
 
'''vladimir.shelomovskii@gmail.com, vvsss'''

Revision as of 04:01, 8 August 2023

The Spieker center is defined as the center of mass of the perimeter of the triangle. The Spieker center of a $\triangle ABC$ is the center of gravity of a homogeneous wire frame in the shape of $\triangle ABC.$ The Spieker center is a triangle center and it is listed as the point $X_{10}.$

Incenter of medial triangle

Physical proof.png

Prove that the Spieker center of triangle $\triangle ABC$ is the incenter of the medial triangle $\triangle DEF$ of a $\triangle ABC.$

Proof

Let's hang up the $\triangle ABC$ in the middle of side $BC.$ Side $BC$ is balanced.

Let's replace side $AC$ with point $E$ (the center of mass of $AC,$ the midpoint $AC).$ Denote $\rho$ the linear density of a homogeneous wire frame.

The mass of point $E$ is equal to $\rho \cdot AC,$ the shoulder of the gravity force is $EE' = ED \sin \alpha = \frac {AB \sin \alpha }{2}.$

The moment of this force is $g EE' \rho \cdot AC = \frac {g \rho\cdot AC \cdot AB}{2} \sin \alpha.$

Similarly the moment gravity force acting on AB is $\frac {g \rho\cdot AC \cdot AB}{2} \sin \beta.$

Therefore, equilibrium condition is $\alpha = \beta$ and the center of gravity of a homogeneous wire frame $ABC$ lies on each bisector of $\triangle DEF.$

This point is the incenter of the medial triangle $\triangle DEF.$

vladimir.shelomovskii@gmail.com, vvsss

Intersection of three cleavers

Cleaver.png

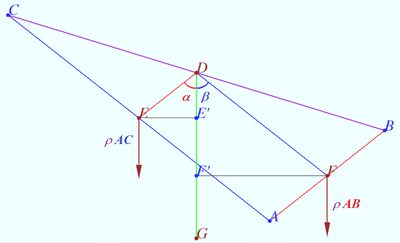
Prove that the Spieker center is located at the intersection of the three cleavers of triangle. A cleaver of a triangle is a line segment that bisects the perimeter of the triangle and has one endpoint at the midpoint of one of the three sides.

Proof

We use notation of previous proof. $DG$ is the segment contains the Spieker center, $G \in AB, \angle EDG = \angle FDG, H = DG \cap AC.$ WLOG, $AC > AB.$ \[DF||AC \implies \angle AHG = \angle FDG.\] Similarly, $\angle AGH = \angle EDG = \angle AHG.$

So $AH = AG \implies CH = AB + AH \implies DH$ is cleaver.

Therefore, the three cleavers meet at the Spieker center.

vladimir.shelomovskii@gmail.com, vvsss

Radical center of excircles

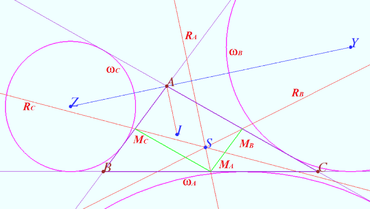
Radical center.png

Prove that the Spieker center of triangle is the radical center of the three excircles.

Proof

Let $\triangle ABC$ be given,$M_A, M_B, M_C$ be the midpoints of $BC, AC, BC,$ respectively.

Let $\omega_A, \omega_B, \omega_C$ be A-excircle, B-excircle, C-excircle centered at $X,Y,Z,$ respectively.

Let $I$ be the incenter of $\triangle ABC.$ Let $R_A$ be the radical axis of $\omega_B$ and $\omega_C, R_B$ be the radical axis of $\omega_A$ and $\omega_C, R_C$ be the radical axis of $\omega_B$ and $\omega_A,$ respectively.

It is known that the distances from $B$ to the tangent points of $\omega_C$ is equal to the distances from $C$ to the tangent points of $\omega_B, BM_A = CM_A$ therefore $M_A$ lies on the radical axis $R_A$ of $\omega_B$ and $\omega_C.$ Similarly, $M_B \in R_B, M_C \in R_C.$

$AI \perp ZY, R_A \perp XY \implies AI || RA \implies R_A$ is cleaver. Similarly, $R_B$ and $R_C$ are cleavers.

Therefore the radical center of the three excircles coinside with the intersection of the three cleavers of triangle.

vladimir.shelomovskii@gmail.com, vvsss

Nagel line

Nagel line.png

Let points $I, G, S$ be the incenter, the centroid and the Spieker center of triangle $\triangle ABC,$ respectively. Prove that points $I, G, S$ are collinear, $IG = 2 GS,$ and the barycentric coordinates of S are ${ b+c : c+a : a+b.}$

The Nagel line is the line on which points $I, G, S,$ and Nagel point $N$ lie.

Proof

Let $D, E, F$ be the midpoints of $BC, AC, BC,$ respectively. Bisector $AI$ is parallel to cleaver $DS, BI || ES.$ \[AB ||ED, \frac {AB}{DE} = 2 \implies \triangle ABI \sim \triangle DES \implies \frac {AI}{DS} = 2.\] Centroid $G$ divide the median $AD$ such that $\frac {AG}{DG} = 2 \implies$

$\triangle AGI \sim \triangle DGS \implies \frac {GI}{SG} = 2,$ and points $I, G, S$ are collinear.

The barycentric coordinates of $I$ are ${a : b : c}.$ The barycentric coordinates of $G$ are ${1 : 1 : 1}.$

\[\vec {GI} = 2 \vec {SG} \implies \vec {G} - \vec {I} = 2(\vec {S} - \vec {G}) \implies\] \[\vec {G} = \frac {3 \vec {G} - \vec {I} }{2} = {1 - \frac{a}{a+ b+c} : 1 - \frac {b}{a+b+c} : 1 - \frac{c}{a+b+c}} = { b+c : c+a : a+b.}\]

vladimir.shelomovskii@gmail.com, vvsss

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Spieker_center&oldid=196616"