Difference between revisions of "2023 AIME II Problems/Problem 12"
(→Solution 3 (simplest)) |
(→Solution 3 (simplest)) |
||
| Line 131: | Line 131: | ||
Notice that the problem statement tells us that point Q is <math>\textit{unique.}</math> EVERY piece of information in the problem statement is intentional, so we should try to use this to our benefit. None of the other solutions do, which is why they are more complicated than they need be. | Notice that the problem statement tells us that point Q is <math>\textit{unique.}</math> EVERY piece of information in the problem statement is intentional, so we should try to use this to our benefit. None of the other solutions do, which is why they are more complicated than they need be. | ||
| − | Consider point Q' s.t. <math>Q'M = MP</math>. Obviously, <math>\angle Q'CP</math> and <math>\angle Q'BP</math> are equal - we have perfect symmetry along line <math>AP</math>. Moreover, <math>BQ'CP</math> is a parallelogram as its diagonals bisect each other. Since point <math>Q</math> is unique, we know that <math>Q' \textit{is} Q</math>. Thus <math>BQCP</math> is a parallelogram. | + | Consider point Q' s.t. <math>Q'M = MP</math>. Obviously, <math>\angle Q'CP</math> and <math>\angle Q'BP</math> are equal - we have perfect symmetry along line <math>AP</math>. Moreover, <math>BQ'CP</math> is a parallelogram as its diagonals bisect each other. Since point <math>Q</math> is unique, we know that <math>Q' \textit{is } Q</math>. Thus <math>BQCP</math> is a parallelogram. <math>\blacksquare</math> |
<math>\newline</math> | <math>\newline</math> | ||
| − | <math>\textbf{ | + | <math>\textbf{Rigorous proof (not recommended for competition scenario):}</math> |
Consider any quadrilateral <math>ABCD</math> whose diagonals intersect at <math>O</math> s.t. <math>AO = OC</math> and <math>\angle BAD = \angle BCD</math>. We will prove that <math>ABCD</math> is <math>\textit{either a \textbf{parallelogram} or a \textbf{kite}}</math>. | Consider any quadrilateral <math>ABCD</math> whose diagonals intersect at <math>O</math> s.t. <math>AO = OC</math> and <math>\angle BAD = \angle BCD</math>. We will prove that <math>ABCD</math> is <math>\textit{either a \textbf{parallelogram} or a \textbf{kite}}</math>. | ||
| − | (Note that in our problem, since <math>AP</math> and <math>BC</math> are not orthogonal (<math>ABC</math> isn't | + | (Note that in our problem, since <math>AP</math> and <math>BC</math> are not orthogonal (<math>ABC</math> isn't isosceles) this is enough to show that <math>BQCP</math> is a parallelogram). |
<math>\newline</math> | <math>\newline</math> | ||
| − | -- By same base/same altitude, <math>[ABO] = [CBO]</math> and <math>[ADO] = [CDO] \implies [ABD] = [ABO] + [ADO] = [CBO] + [CDO] = [CBD] \newline</math> | + | -- By same base/same altitude, <math>[ABO] = [CBO]</math> and <math>[ADO] = [CDO] \implies [ABD] = [ABO] + [ADO] = [CBO] + [CDO] = [CBD]. \newline</math> |
| − | Therefore: <math>\frac{1}{2} sin(\angle BAD) \overline{AB} \times \overline{AD} = \frac{1}{2} sin(\angle BCD) \overline{CB} \times \overline{CD}.</math> Since | + | Therefore: <math>\frac{1}{2} sin(\angle BAD) \overline{AB} \times \overline{AD} = \frac{1}{2} sin(\angle BCD) \overline{CB} \times \overline{CD}.</math> Since <math>\angle BAD = \angle BCD</math>, this reduces to <math>\overline{AB} \times \overline{AD} = \overline{CB} \times \overline{CD}.\newline</math> |
| − | Let < | + | Let <math>AB = x</math>, <math>AD = y</math>, <math>CB = kx</math>, <math>CD = \frac{y}{k}</math>. Then by LoC on <math>\triangle BAD</math> and <math>\triangle BCD</math>: |
| − | < | + | <math>x^{2} + y^{2} - 2xy cos(\angle BAD) = \overline{BD} = x^{2}k^{2} + \frac{y^{2}}{k^{2}} - 2xy cos(\angle BCD) \newline \implies x^{2} + y^{2} = x^{2}k^{2} + \frac{y^{2}}{k^{2}} \newline \implies (y^{2} - x^{2}k^{2})(k^{2} - 1) = 0.\newline</math> |
| − | -- < | + | -- <math>y^{2} - x^{2}k^{2} = 0 \implies y = kx \implies AD = BC</math> and <math>AB = CD \implies</math> <math>ABCD</math> is a parallelogram. |
| − | -- < | + | |
| + | -- <math>k^{2} - 1 = 0 \implies k = 1</math> (<math>k</math> cannot be <math>-1</math>; no negative sided polygons here!) <math>\implies AB = CB</math> and <math>AD = CD \implies</math> <math>ABCD</math> is a kite. <math>\square</math>. ~Mathavi | ||
==Solution 4 (LOS+ coordbash)== | ==Solution 4 (LOS+ coordbash)== | ||
Revision as of 14:18, 21 November 2023
Contents
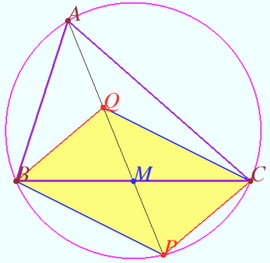
[hide]Problem
In ![]() with side lengths
with side lengths ![]()
![]() and
and ![]() let
let ![]() be the midpoint of
be the midpoint of ![]() Let
Let ![]() be the point on the circumcircle of
be the point on the circumcircle of ![]() such that
such that ![]() is on
is on ![]() There exists a unique point
There exists a unique point ![]() on segment
on segment ![]() such that
such that ![]() Then
Then ![]() can be written as
can be written as ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
Solution 1
Because ![]() is the midpoint of
is the midpoint of ![]() , following from the Steward's theorem,
, following from the Steward's theorem, ![]() .
.
Because ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are concyclic,
are concyclic, ![]() ,
, ![]() .
.
Denote ![]() .
.
In ![]() , following from the law of sines,
, following from the law of sines,
![]()
Thus,
![]()
In ![]() , following from the law of sines,
, following from the law of sines,
![]()
Thus,
![]()
Taking ![]() , we get
, we get
![]()
In ![]() , following from the law of sines,
, following from the law of sines,
![]()
Thus, Equations (2) and (3) imply

Next, we compute ![]() and
and ![]() .
.
We have

We have

Taking (5) and (6) into (4), we get ![]()
Therefore, the answer is ![]()
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
Solution 2
Define ![]() to be the foot of the altitude from
to be the foot of the altitude from ![]() to
to ![]() . Furthermore, define
. Furthermore, define ![]() to be the foot of the altitude from
to be the foot of the altitude from ![]() to
to ![]() . From here, one can find
. From here, one can find ![]() , either using the 13-14-15 triangle or by calculating the area of
, either using the 13-14-15 triangle or by calculating the area of ![]() two ways. Then, we find
two ways. Then, we find ![]() and
and ![]() using Pythagorean theorem. Let
using Pythagorean theorem. Let ![]() . By AA similarity,
. By AA similarity, ![]() and
and ![]() are similar. By similarity ratios,
are similar. By similarity ratios, ![]()
![]()
![]() Thus,
Thus, ![]() . Similarly,
. Similarly, ![]() . Now, we angle chase from our requirement to obtain new information.
. Now, we angle chase from our requirement to obtain new information.
![]()
![]()
![]()
![]()
![]()
![]()
![]() Take the tangent of both sides to obtain
Take the tangent of both sides to obtain
![]() By the definition of the tangent function on right triangles, we have
By the definition of the tangent function on right triangles, we have ![]() ,
, ![]() , and
, and ![]() . By abusing the tangent angle addition formula, we can find that
. By abusing the tangent angle addition formula, we can find that
![]() By substituting
By substituting ![]() ,
, ![]() and using tangent angle subtraction formula we find that
and using tangent angle subtraction formula we find that
![]() Finally, using similarity formulas, we can find
Finally, using similarity formulas, we can find
![]() . Plugging in
. Plugging in ![]() and
and ![]() , we find that
, we find that ![]() Thus, our final answer is
Thus, our final answer is ![]() .
~sigma
.
~sigma
Solution 3 (simplest)
It is clear that ![]() is a parallelogram. By Stewart's Theorem,
is a parallelogram. By Stewart's Theorem, ![]() , POP on
, POP on ![]() tells
tells ![]()
As ![]() leads to
leads to ![]()
~bluesoul (supplemental note: ~Mathavi)
![]()
It's not actually immediately clear why this is the case. There are two ways to easily show this:
![]()
Notice that the problem statement tells us that point Q is ![]() EVERY piece of information in the problem statement is intentional, so we should try to use this to our benefit. None of the other solutions do, which is why they are more complicated than they need be.
EVERY piece of information in the problem statement is intentional, so we should try to use this to our benefit. None of the other solutions do, which is why they are more complicated than they need be.
Consider point Q' s.t. ![]() . Obviously,
. Obviously, ![]() and
and ![]() are equal - we have perfect symmetry along line
are equal - we have perfect symmetry along line ![]() . Moreover,
. Moreover, ![]() is a parallelogram as its diagonals bisect each other. Since point
is a parallelogram as its diagonals bisect each other. Since point ![]() is unique, we know that
is unique, we know that ![]() . Thus
. Thus ![]() is a parallelogram.
is a parallelogram. ![]()
![]()
![]() Consider any quadrilateral
Consider any quadrilateral ![]() whose diagonals intersect at
whose diagonals intersect at ![]() s.t.
s.t. ![]() and
and ![]() . We will prove that
. We will prove that ![]() is
is ![]() .
.
(Note that in our problem, since ![]() and
and ![]() are not orthogonal (
are not orthogonal (![]() isn't isosceles) this is enough to show that
isn't isosceles) this is enough to show that ![]() is a parallelogram).
is a parallelogram).
![]() -- By same base/same altitude,
-- By same base/same altitude, ![]() and
and ![]()
Therefore: ![]() Since
Since ![]() , this reduces to
, this reduces to ![]()
Let ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Then by LoC on
. Then by LoC on ![]() and
and ![]() :
:

-- ![]() and
and ![]()
![]() is a parallelogram.
is a parallelogram.
-- ![]() (
(![]() cannot be
cannot be ![]() ; no negative sided polygons here!)
; no negative sided polygons here!) ![]() and
and ![]()
![]() is a kite.
is a kite. ![]() . ~Mathavi
. ~Mathavi
Solution 4 (LOS+ coordbash)
First, note that by Law of Sines, ![]() and that
and that ![]() . Equating the 2 expressions, you get that
. Equating the 2 expressions, you get that ![]() . Now drop the altitude from
. Now drop the altitude from ![]() to
to ![]() . As it is commonly known that the dropped altitude forms a
. As it is commonly known that the dropped altitude forms a ![]() and a
and a ![]() triangle, you get the measures of
triangle, you get the measures of ![]() and
and ![]() respectively, which are
respectively, which are ![]() and
and ![]() . However, by the inscribed angle theorem, you get that
. However, by the inscribed angle theorem, you get that ![]() and that
and that ![]() , respectively. Therefore, by Law of Sines (as previously stated)
, respectively. Therefore, by Law of Sines (as previously stated) ![]() .
.
Now commence coordbashing. Let ![]() be the origin, and
be the origin, and ![]() be the point
be the point ![]() . As
. As ![]() passes through
passes through ![]() , which is
, which is ![]() , and
, and ![]() , which is
, which is ![]() , it has the equation
, it has the equation ![]() , so therefore a point on this line can be written as
, so therefore a point on this line can be written as ![]() . As we have the ratio of the lengths, which prompts us to write the lengths in terms of the distance formula, we can just plug and chug it in to get the ratio
. As we have the ratio of the lengths, which prompts us to write the lengths in terms of the distance formula, we can just plug and chug it in to get the ratio ![]() . This can be squared to get
. This can be squared to get ![]() . This can be solved to get a solution of
. This can be solved to get a solution of ![]() , and an extraneous solution of
, and an extraneous solution of ![]() which obviously doesn’t work.
which obviously doesn’t work.
Plugging ![]() into the line equation gets you
into the line equation gets you ![]() . The distance between this point and
. The distance between this point and ![]() , which is
, which is ![]() is
is ![]() , or simplified to
, or simplified to ![]()
~dragoon (minor ![]() fixes by rhydon516)
fixes by rhydon516)
Solution 5 (similar to 3)
We use the law of Cosine and get ![]()
![]()
![]() We use the power of point
We use the power of point ![]() with respect circumcircle
with respect circumcircle ![]() and get
and get
![]()
![]() It is clear that if
It is clear that if ![]() then
then ![]()
if ![]() is simmetric to
is simmetric to ![]() with respect
with respect ![]() then
then ![]()
There exists a unique point ![]() on segment
on segment ![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Video Solution 1 by SpreadTheMathLove
https://www.youtube.com/watch?v=k6hEFEVVzMI
See also
| 2023 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 11 |
Followed by Problem 13 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.