Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Mock AIME 6 2006-2007 Problems/Problem 13"
Line 38: Line 38:
 
Then, <math>A_1=r_1s=s=\frac{|AB|+\sqrt{(h+d)^2-r_2^2}+\sqrt{h^2-r_1^2}}{2}=\frac{20\sqrt{2}+\left( \frac{r_2}{r_1}+1 \right)\sqrt{h^2-r_1^2}}{2}</math>
 
Then, <math>A_1=r_1s=s=\frac{|AB|+\sqrt{(h+d)^2-r_2^2}+\sqrt{h^2-r_1^2}}{2}=\frac{20\sqrt{2}+\left( \frac{r_2}{r_1}+1 \right)\sqrt{h^2-r_1^2}}{2}</math>
  
 +
<math>A_1=\frac{20\sqrt{2}+12\sqrt{3^2-1^2}}{2}=10\sqrt{2}+12\sqrt{2}=22\sqrt{2}</math>
  
 
~Tomas Diaz. orders@tomasdiaz.com
 
~Tomas Diaz. orders@tomasdiaz.com
  
 
{{alternate solutions}}
 
{{alternate solutions}}

Revision as of 02:33, 26 November 2023

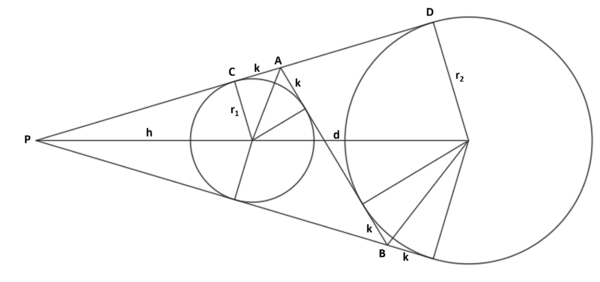
Problem

Consider two circles of different sizes that do not intersect. The smaller circle has center $O$. Label the intersection of their common external tangents $P$. A common internal tangent intersects the common external tangents at points $A$ and $B$. Given that the radius of the larger circle is $11$, $PO=3$, and $AB=20\sqrt{2}$, what is the square of the area of triangle $PBA$?

Solution

Mock AIME 6 P13a.png

$|AB|=|CD|=20\sqrt{2}$

Let $d$ be the distance between centers, and $h=|PO|=3$

$|CD|^2+(r_2-r_1)^2=d^2$

$(20\sqrt{2})^2+(r_2-r_1)^2=d^2$

$800+(r_2-r_1)^2=d^2$ [Equation 1]

By similar triangles,

$\frac{r_1}{h}=\frac{r_2}{h+d}$

solving for $d$ we have:

$d=\frac{(r_2-r_1)h}{r_1}$ [Equation 2]

Substituting [Equation 2] into [Equation 1] we have:

$800+(r_2-r_1)^2=\frac{(r_2-r_1)^2h^2}{r_1^2}$

$800+(11-r_1)^2=\frac{9(11-r_1)^2}{r_1^2}$

Solving for $r_1$ we get $r_1=1$

Since $r_1$ is the radius of the incircle of $\Delta PBA$ then,

$r_1=\frac{A_1}{s}$ where $A_1$ is the area of $\Delta PBA$ and $s$ is half the perimeter of $\Delta PBA$

Then, $A_1=r_1s=s=\frac{|AB|+\sqrt{(h+d)^2-r_2^2}+\sqrt{h^2-r_1^2}}{2}=\frac{20\sqrt{2}+\left( \frac{r_2}{r_1}+1 \right)\sqrt{h^2-r_1^2}}{2}$

$A_1=\frac{20\sqrt{2}+12\sqrt{3^2-1^2}}{2}=10\sqrt{2}+12\sqrt{2}=22\sqrt{2}$

~Tomas Diaz. orders@tomasdiaz.com

Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Mock_AIME_6_2006-2007_Problems/Problem_13&oldid=205866"