Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Mock AIME 6 2006-2007 Problems/Problem 13"
 
(9 intermediate revisions by the same user not shown)
Line 1: Line 1:
 
==Problem==
 
==Problem==
−
Consider two circles of different sizes that do not intersect.  The smaller circle has center <math>O</math>.  Label the intersection of their common external tangents <math>P</math>.  A common internal tangent interesects the common external tangents at points <math>A</math> and <math>B</math>.  Given that the radius of the larger circle is <math>11</math>, <math>PO=3</math>, and <math>AB=20\sqrt{2}</math>, what is the square of the area of triangle <math>PBA</math>?
+
Consider two circles of different sizes that do not intersect.  The smaller circle has center <math>O</math>.  Label the intersection of their common external tangents <math>P</math>.  A common internal tangent intersects the common external tangents at points <math>A</math> and <math>B</math>.  Given that the radius of the larger circle is <math>11</math>, <math>PO=3</math>, and <math>AB=20\sqrt{2}</math>, what is the square of the area of triangle <math>PBA</math>?
  
 
==Solution==
 
==Solution==
  
−
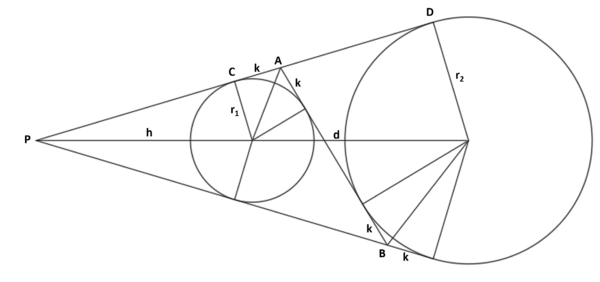
[[File:Mock_AIME_6_P13.png|600px]]
+
[[File:Mock_AIME_6_P13a.png|600px]]
 +
 
 +
<math>|AB|=|CD|=20\sqrt{2}</math>
 +
 
 +
Let <math>d</math> be the distance between centers, and <math>h=|PO|=3</math>
 +
 
 +
<math>|CD|^2+(r_2-r_1)^2=d^2</math>
 +
 
 +
<math>(20\sqrt{2})^2+(r_2-r_1)^2=d^2</math>
 +
 
 +
<math>800+(r_2-r_1)^2=d^2</math> [Equation 1]
 +
 
 +
By similar triangles,
 +
 
 +
<math>\frac{r_1}{h}=\frac{r_2}{h+d}</math>
 +
 
 +
solving for <math>d</math> we have:
 +
 
 +
<math>d=\frac{(r_2-r_1)h}{r_1}</math> [Equation 2]
 +
 
 +
Substituting [Equation 2] into [Equation 1] we have:
 +
 
 +
<math>800+(r_2-r_1)^2=\frac{(r_2-r_1)^2h^2}{r_1^2}</math>
 +
 
 +
<math>800+(11-r_1)^2=\frac{9(11-r_1)^2}{r_1^2}</math>
 +
 
 +
Solving for <math>r_1</math> we get <math>r_1=1</math>
 +
 
 +
Since <math>r_1</math> is the radius of the incircle of <math>\Delta PBA</math> then,
 +
 
 +
<math>r_1=\frac{A_1}{s}</math> where <math>A_1</math> is the area of <math>\Delta PBA</math> and <math>s</math> is half the perimeter of <math>\Delta PBA</math>
 +
 
 +
Then, <math>A_1=r_1s=s=\frac{|AB|+(\sqrt{(h+d)^2-r_2^2}-k)+(\sqrt{h^2-r_1^2}+k)}{2}=\frac{20\sqrt{2}+\left( \frac{r_2}{r_1}+1 \right)\sqrt{h^2-r_1^2}}{2}</math>
 +
 
 +
<math>A_1=\frac{20\sqrt{2}+12\sqrt{3^2-1^2}}{2}=10\sqrt{2}+12\sqrt{2}=22\sqrt{2}</math>
 +
 
 +
<math>A_1^2=(22\sqrt{2})^2=\boxed{968}</math>
  
 
~Tomas Diaz. orders@tomasdiaz.com
 
~Tomas Diaz. orders@tomasdiaz.com
  
 
{{alternate solutions}}
 
{{alternate solutions}}

Latest revision as of 02:36, 26 November 2023

Problem

Consider two circles of different sizes that do not intersect. The smaller circle has center $O$. Label the intersection of their common external tangents $P$. A common internal tangent intersects the common external tangents at points $A$ and $B$. Given that the radius of the larger circle is $11$, $PO=3$, and $AB=20\sqrt{2}$, what is the square of the area of triangle $PBA$?

Solution

Mock AIME 6 P13a.png

$|AB|=|CD|=20\sqrt{2}$

Let $d$ be the distance between centers, and $h=|PO|=3$

$|CD|^2+(r_2-r_1)^2=d^2$

$(20\sqrt{2})^2+(r_2-r_1)^2=d^2$

$800+(r_2-r_1)^2=d^2$ [Equation 1]

By similar triangles,

$\frac{r_1}{h}=\frac{r_2}{h+d}$

solving for $d$ we have:

$d=\frac{(r_2-r_1)h}{r_1}$ [Equation 2]

Substituting [Equation 2] into [Equation 1] we have:

$800+(r_2-r_1)^2=\frac{(r_2-r_1)^2h^2}{r_1^2}$

$800+(11-r_1)^2=\frac{9(11-r_1)^2}{r_1^2}$

Solving for $r_1$ we get $r_1=1$

Since $r_1$ is the radius of the incircle of $\Delta PBA$ then,

$r_1=\frac{A_1}{s}$ where $A_1$ is the area of $\Delta PBA$ and $s$ is half the perimeter of $\Delta PBA$

Then, $A_1=r_1s=s=\frac{|AB|+(\sqrt{(h+d)^2-r_2^2}-k)+(\sqrt{h^2-r_1^2}+k)}{2}=\frac{20\sqrt{2}+\left( \frac{r_2}{r_1}+1 \right)\sqrt{h^2-r_1^2}}{2}$

$A_1=\frac{20\sqrt{2}+12\sqrt{3^2-1^2}}{2}=10\sqrt{2}+12\sqrt{2}=22\sqrt{2}$

$A_1^2=(22\sqrt{2})^2=\boxed{968}$

~Tomas Diaz. orders@tomasdiaz.com

Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Mock_AIME_6_2006-2007_Problems/Problem_13&oldid=205869"