Difference between revisions of "Talk:2024 AIME I Problems/Problem 12"
(→Solution 1 seems a bit deceptive: new section) |
(→RE: Solution 1: new section) |
||
| Line 19: | Line 19: | ||
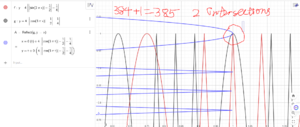
How can one possibly count hundreds of intersections??? | How can one possibly count hundreds of intersections??? | ||
| + | |||
| + | == RE: Solution 1 == | ||
| + | |||
| + | Don't ask. I spend 20 minutes of my life drawing that graph during AIME and I am NOT doing it again | ||
Latest revision as of 14:15, 4 February 2024
This problem's answer is wrong. When I completed this test, I did this problem wrong, too, because I missed this crucial (and weird) thing as mentioned below.
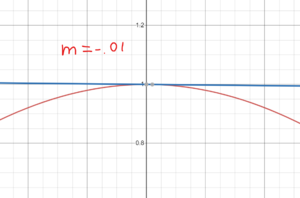
It is a very bad problem because there is actually another intersection if you look closely in Geogebra or other drawing tools. It is nearly impossible for humans to find.
Near the point (1, 1), not only is there an intersection at point (1, 1), but also another intersection at around (0.99, 0.99).
Here is the graph for proof:
RE: Bad graph
Note that although solution 1 is the first solution, it is not necessarily the intended one (which it probably isn't). I also acknowledged this in the note section, and should be hard to notice, as a hump and a non-zero sloped line that passes through its peak must also pass through another point of the hump.
Also this doesn't immediately mean that this is a bad problem.
Solution 1 seems a bit deceptive
How can one possibly count hundreds of intersections???
RE: Solution 1
Don't ask. I spend 20 minutes of my life drawing that graph during AIME and I am NOT doing it again