Difference between revisions of "Steiner line"
(→Steiner line) |
m (→Steiner line) |
||
| (14 intermediate revisions by one other user not shown) | |||
| Line 21: | Line 21: | ||
Let <math>\angle ABC = \beta, \angle BFD = \varphi \implies \angle BDF = \beta – \varphi.</math> | Let <math>\angle ABC = \beta, \angle BFD = \varphi \implies \angle BDF = \beta – \varphi.</math> | ||
<cmath>P_CP_A||DF \implies \angle P_CYB = \beta – \varphi.</cmath> | <cmath>P_CP_A||DF \implies \angle P_CYB = \beta – \varphi.</cmath> | ||
| − | <math>P</math> is | + | <math>P</math> is symmetric to <math>P_C \implies \angle PYD = \beta – \varphi.</math> |
| − | + | Quadrangle <math>BDPF</math> is cyclic <math>\implies \angle BPD = \varphi \implies \angle BPY = 90^\circ – \angle BYP – \angle BPD = 90^\circ – \beta.</math> | |
<math>\angle BCH = \angle BPY \implies PY \cap CH</math> at point <math>H_C \in \Omega.</math> | <math>\angle BCH = \angle BPY \implies PY \cap CH</math> at point <math>H_C \in \Omega.</math> | ||
| Line 56: | Line 56: | ||
Usually the point <math>P</math> is called the anti-Steiner point of the <math>H-line</math> with respect to <math>\triangle ABC.</math> | Usually the point <math>P</math> is called the anti-Steiner point of the <math>H-line</math> with respect to <math>\triangle ABC.</math> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Ortholine== | ||
| + | [[File:Ortholine.png|400px|right]] | ||
| + | Let four lines made four triangles of a complete quadrilateral. | ||
| + | |||
| + | In the diagram these are <math>\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.</math> | ||
| + | |||
| + | Let points <math>H, H_A, H_B,</math> and <math>H_C</math> be the orthocenters of <math>\triangle ABC, \triangle ADE, \triangle BDF,</math> and <math>\triangle CEF,</math> respectively. | ||
| + | |||
| + | Prove that points <math>H, H_A, H_B,</math> and <math>H_C</math> are collinear. | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Let <math>M</math> be Miquel point of a complete quadrilateral. | ||
| + | |||
| + | Line <math>KLMN</math> is the line which contain <math>4</math> Simson lines of <math>4</math> triangles. | ||
| + | |||
| + | Using homothety centered at <math>M</math> with ratio <math>2</math> we get <math>4</math> coinciding Stainer lines which contain points <math>H, H_A, H_B,</math> and <math>H_C</math>. | ||
| + | |||
| + | *[[Miquel's point]] | ||
| + | *[[Simson line]] | ||
| + | |||
| + | <i><b>Proof 2</b></i> | ||
| + | [[File:Steiner 2.png|400px|right]] | ||
| + | <math>AH_A \perp DE, CH_C \perp EF \implies AH_A ||CH_C,</math> | ||
| + | |||
| + | <math>AH \perp BC, EH_C \perp CF \implies AH ||EH_C,</math> | ||
| + | |||
| + | <math>EH_A \perp AD, CH \perp AB \implies EH_A ||CH.</math> | ||
| + | |||
| + | Points <math>A, E,</math> and <math>C</math> are collinear. | ||
| + | |||
| + | According the <i><b>Claim of parallel lines,</b></i> points <math>H, H_A,</math> and <math>H_C</math> are collinear. | ||
| + | |||
| + | Similarly points <math>H, H_B,</math> and <math>H_C</math> are collinear as desired. | ||
| + | |||
| + | <i><b>Claim of parallel lines</b></i> | ||
| + | |||
| + | Let points <math>A, B,</math> and <math>C</math> be collinear. | ||
| + | |||
| + | Let points <math>D, E, F</math> be such that <math>AF||CD, BF||CE, AE||BD.</math> | ||
| + | |||
| + | Prove that points <math>D, E,</math> and <math>F</math> are collinear. | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | [[File:Pras 1 12.png|400px|right]] | ||
| + | Let <math>P = AE \cap CD, Q = AF \cap CE.</math> | ||
| + | |||
| + | <cmath>\angle CEP = \angle QEA, AQ||CP \implies \angle QAE = \angle CPE \implies</cmath> | ||
| + | <cmath>\triangle AEQ \sim \triangle PEC.</cmath> | ||
| + | |||
| + | <cmath>AP||BD \implies \frac {PD}{CD} = \frac {AB}{BC},</cmath> | ||
| + | |||
| + | <cmath>CQ||BF \implies \frac {AF}{QF} = \frac {AB}{BC} = \frac {PD}{CD}.</cmath> | ||
| + | |||
| + | The segments <math>EF</math> and <math>ED</math> are corresponding segments in similar triangles. | ||
| + | Therefore <math>\angle CED = \angle QEF \implies D, E,</math> and <math>F</math> are collinear. | ||
| + | *[[Complete Quadrilateral]] | ||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Shatunov-Tokarev line== | ||
| + | [[File:Shatunov line.png|500px|right]] | ||
| + | Let the quadrilateral <math>ABCD</math> be given (<math>ABCD</math> is not cyclic). Let points <math>E</math> and <math>F</math> be the midpoints of <math>BD</math> and <math>AC,</math> respectively. Let points <math>P</math> and <math>Q</math> be such points that <math>PA = PB, PC = PD, QA = QD, QB = QC.</math> | ||
| + | |||
| + | a) Prove that <math>PQ \perp EF.</math> | ||
| + | |||
| + | b) Prove that the point <math>X</math> lies on the line <math>PQ</math> iff <math>XA^2 + XC^2 = XB^2 + XD^2.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | a) Let <math>\omega</math> be the circle centered at <math>F</math> with radius <math>BE.</math> Let <math>\Omega</math> be the circle centered at <math>E</math> with radius <math>AF.</math> | ||
| + | <math>PE</math> is the median of <math>\triangle PBD \implies PE^2 = \frac {PB^2 + PD^2}{2} – BE^2.</math> | ||
| + | |||
| + | The power of the point <math>P</math> with respect to the circle <math>\Omega</math> is <math>Pow_{\Omega}(P) = PE^2 – AF^2 = \frac {PB^2 + PD^2}{2} – BE^2 – AF^2.</math> | ||
| + | |||
| + | <math>PF</math> is the median of <math>\triangle PAC \implies PF^2 = \frac {PA^2 + PC^2}{2} – AF^2.</math> | ||
| + | |||
| + | The power of the point <math>P</math> with respect to the circle <math>\omega</math> is <math>Pow_{\omega}(P) = PF^2 – BE^2 = \frac {PA^2 + PC^2}{2} – BE^2 – AF^2 = \frac {PB^2 + PD^2}{2} – BE^2 – AF^2 = Pow_{\Omega}(P).</math> | ||
| + | |||
| + | Therefore <math>P</math> lies on the radical axis of <math>\Omega</math> and <math>\omega.</math> Similarly, <math>Q</math> lies on these line. | ||
| + | So the line <math>PQ</math> is the radical axes of <math>\Omega</math> and <math>\omega.</math> | ||
| + | |||
| + | This line is perpendicular to Gauss line <math>EF</math> which is the line of centers of two circles <math>\Omega</math> and <math>\omega</math> as desired. | ||
| + | |||
| + | b) <math>XE</math> is the median of <math>\triangle XBD \implies XE^2 = \frac {XB^2 + XD^2}{2} – BE^2.</math> | ||
| + | |||
| + | <math>XF</math> is the median of <math>\triangle XAC \implies XF^2 = \frac {XA^2 + XC^2}{2} – AF^2.</math> | ||
| + | |||
| + | <math>X</math> lies on the radical axes of <math>\Omega</math> and <math>\omega \implies XE^2 – XF^2 = AF^2 – BE^2 \implies</math> | ||
| + | <cmath>\frac {XB^2 + XD^2}{2} – BE^2 – ( \frac {XA^2 + XC^2}{2} – AF^2) = AF^2 – BE^2 \implies XB^2 + XD^2 = XA^2 + XC^2.</cmath> | ||
| + | |||
| + | If the point <math>X</math> satisfies the equation <math>XB^2 + XD^2 = XA^2 + XC^2</math> then locus of <math>X</math> is the straight line (one can prove it using method of coordinates). | ||
| + | |||
| + | The points <math>P</math> and <math>Q</math> are satisfies this equation, so this line contain these points as desired. | ||
| + | |||
| + | It is easy to understand that this line is parallel to Steiner line which is the radical axis of the circles centered at <math>E</math> and <math>F</math> with radii <math>BE</math> and <math>AF,</math> respectively. | ||
| + | |||
| + | Of course, it is parallel to Simson line. | ||
| + | *[[Complete Quadrilateral]] | ||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Shatunov-Tokarev concurrent lines== | ||
| + | [[File:Shatunov 3 concurrent lines.png|500px|right]] | ||
| + | Let the quadrilateral <math>ABCD</math> be given (<math>ABCD</math> is not cyclic). | ||
| + | |||
| + | Let points <math>A'</math> and <math>A''</math> be on the line <math>AB</math> such that <math>AA' = AA''</math>. Similarly | ||
| + | <cmath>B' \in BC, B'' \in BC, C' \in CD, C'' \in CD,</cmath> | ||
| + | <cmath>D' \in AD, D'' \in AD,</cmath> | ||
| + | <cmath>BB' = BB'' = CC' = CC'' = DD' = DD'' = AA'.</cmath> | ||
| + | |||
| + | Let points <math>Q, Q',</math> and <math>Q''</math> be the crosspoints of the bisectors <math>AD \cap BC, A'D' \cap B'C', A''D'' \cap B''C''.</math> | ||
| + | |||
| + | Similarly points <math>P, P',</math> and <math>P''</math> are the crosspoints of the bisectors <math>AB \cap CD, A'B' \cap C'D', A''B'' \cap C''D''.</math> | ||
| + | |||
| + | Prove that lines <math>PQ, P'Q',</math> and <math>P''Q''</math> are concurrent. | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Segment <math>XA</math> is the median of the <math>\triangle XA'A'' \implies 2(XA^2 + AA'^2) = XA'^2 + XA''^2.</math> | ||
| + | |||
| + | Similarly <math>2(XB^2 + BB'^2) = XB'^2 + XB''^2, 2(XC^2 + CC'^2) = XC'^2 + XC''^2, 2(XD^2 + DD'^2) = XD'^2 + XD''^2.</math> | ||
| + | |||
| + | Let <math>PQ</math> cross <math>P'Q'</math> at point <math>X \implies XA^2 + XC^2 = XB^2 + XD^2, XA'^2 + XC'^2 = XB'^2 + XD'^2.</math> | ||
| + | |||
| + | We made simple calculations and get <math>XA''^2 + XC''^2 = XB''^2 + XD''^2,</math> therefore point <math>X</math> lies on <math>P''Q''</math> as desired. | ||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Shatunov point== | ||
| + | [[File:Shatunov point.png|450px|right]] | ||
| + | Let the quadrilateral <math>ABCD</math> be given (<math>ABCD</math> is not cyclic). | ||
| + | |||
| + | Let points <math>A', B', C',</math> and <math>D'</math> be on the lines <math>AD, AB, BC,</math> and <math>CD,</math> respectively such that <math>|AA'| = |BB'| = |CC'| = |DD'| = d.</math> | ||
| + | |||
| + | Let points <math>A'', B'', C'',</math> and <math>D''</math> be on the segments <math>AA', BB', CC',</math> and <math>DD',</math> respectively such that <math>\frac {|AA''|}{|A'A''|} = \frac {|BB''|}{|B'B''|} = \frac {|CC''|}{|C'C''|} = \frac {|DD''|}{|D'D''|} = \frac {m}{n},</math> where <math>m + n = 1.</math> | ||
| + | |||
| + | Let points <math>Q, Q',</math> and <math>Q''</math> be the crosspoints of the bisectors <math>AD \cap BC, A'D' \cap B'C', A''D'' \cap B''C''.</math> | ||
| + | |||
| + | Similarly points <math>P, P',</math> and <math>P''</math> are the crosspoints of the bisectors <math>AB \cap CD, A'B' \cap C'D', A''B'' \cap C''D''.</math> | ||
| + | |||
| + | Prove that lines <math>PQ, P'Q',</math> and <math>P''Q''</math> are concurrent. | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Segment <math>XA''</math> is the cevian to the side AA' of the <math>\triangle XAA'.</math> | ||
| + | |||
| + | We use the Stewart's theorem and get: | ||
| + | <cmath>m \cdot|XA'|^2 + n \cdot |XA|^2) = |XA''|^2 + mn \cdot d^2.</cmath> | ||
| + | Similarly <math> m \cdot|XB'|^2 + n \cdot |XB|^2) = |XB''|^2 + mn \cdot d^2,</math> | ||
| + | <cmath>m \cdot|XC'|^2 + n \cdot |XC|^2) = |XC''|^2 + mn \cdot d^2,</cmath> | ||
| + | <cmath>m \cdot|XD'|^2 + n \cdot |XD|^2) = |XD''|^2 + mn \cdot d^2.</cmath> | ||
| + | Let <math>PQ</math> cross <math>P'Q'</math> at point <math>X \implies |XA|^2 + |XC|^2 = |XB|^2 + |XD|^2, |XA'|^2 + |XC'|^2 = |XB'|^2 + |XD'|^2.</math> | ||
| + | |||
| + | We made simple calculations and get <math>|XA''|^2 + |XC''|^2 = |XB''|^2 + |XD''|^2,</math> therefore point <math>X</math> lies on <math>P''Q''</math> as desired. | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Shatunov chain== | ||
| + | [[File:Shatunov 8 points chain.png|450px|right]] | ||
| + | Let the quadrilateral <math>ABCD</math> be given (<math>ABCD</math> is not cyclic). | ||
| + | |||
| + | Let points <math>A'</math> and <math>A''</math> be on the line <math>AB</math> such that <math>|AA'| = |AA''|</math>. Similarly <math>B' \in BC, B'' \in BC, C' \in CD, C'' \in CD, D' \in AD, D'' \in AD,</math> | ||
| + | <math>|BB'| = |BB''| = |CC'| = |CC''| = |DD'| = |DD''| = |AA'|.</math> | ||
| + | |||
| + | Let points <math>Q</math> and <math>P</math> be the crosspoints of the bisectors <math>AD \cap BC</math> and <math>AB \cap CD.</math> | ||
| + | |||
| + | We made quadrilateral <math>KLMN</math> using one point from the pare <math>{A',A''},</math> one point from the pare <math>{B',B''},</math> one point from the pare <math>{C',C''},</math> one point from the pare <math>{D',D''}.</math> | ||
| + | For each quadrilateral we find the crosspoints of the bisectors <math>KL \cap MN</math> and <math>KN \cap LM</math> and named these points as <math>{Q_i,P_i}, i = 1..16.</math> | ||
| + | |||
| + | Prove that lines <math>P_iQ_i</math> cross line <math>PQ</math> in 8 points and positions of these points are fixed for given <math>ABCD</math> (not depend from the length of <math>AA'.)</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | The claim follows from the fact that there are <math>4^2 = 16</math> combinations of quadrilateral vertices, and these 16 quadrilaterals are divided into pairs whose points of intersection with the line <math>PQ</math> coincide. | ||
'''vladimir.shelomovskii@gmail.com, vvsss''' | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
Latest revision as of 11:07, 12 May 2024
Contents
Steiner line
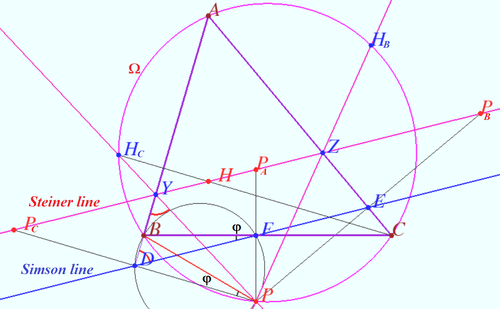
Let ![]() be a triangle with orthocenter
be a triangle with orthocenter ![]() is a point on the circumcircle
is a point on the circumcircle ![]() of
of ![]()
Let ![]() and
and ![]() be the reflections of
be the reflections of ![]() in three lines which contains edges
in three lines which contains edges ![]() and
and ![]() respectively.
respectively.
Prove that ![]() and
and ![]() are collinear. Respective line is known as the Steiner line of point
are collinear. Respective line is known as the Steiner line of point ![]() with respect to
with respect to ![]()
Proof
Let ![]() and
and ![]() be the foots of the perpendiculars dropped from
be the foots of the perpendiculars dropped from ![]() to lines
to lines ![]() and
and ![]() respectively.
respectively.
WLOG, Steiner line cross ![]() at
at ![]() and
and ![]() at
at ![]()
The line ![]() is Simson line of point
is Simson line of point ![]() with respect of
with respect of ![]()
![]() is midpoint of segment
is midpoint of segment ![]() homothety centered at
homothety centered at ![]() with ratio
with ratio ![]() sends point
sends point ![]() to a point
to a point ![]()
Similarly, this homothety sends point ![]() to a point
to a point ![]() , point
, point ![]() to a point
to a point ![]() therefore this homothety send Simson line to line
therefore this homothety send Simson line to line ![]()
Let ![]()
![]()
![]() is symmetric to
is symmetric to ![]()
Quadrangle ![]() is cyclic
is cyclic ![]()
![]() at point
at point ![]() Similarly, line
Similarly, line ![]() at
at ![]()
According the Collins Claim ![]() is
is ![]() therefore
therefore ![]()
vladimir.shelomovskii@gmail.com, vvsss
Collings Clime
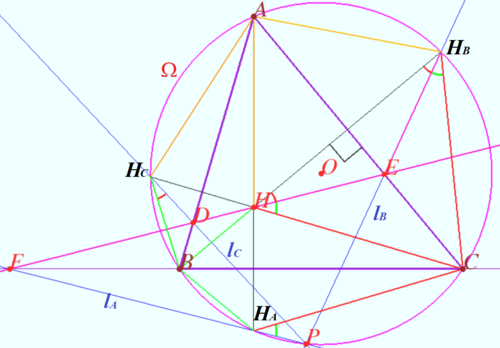
Let triangle ![]() be the triangle with the orthocenter
be the triangle with the orthocenter ![]() and circumcircle
and circumcircle ![]() Denote
Denote ![]() any line containing point
any line containing point ![]()
Let ![]() and
and ![]() be the reflections of
be the reflections of ![]() in the edges
in the edges ![]() and
and ![]() respectively.
respectively.
Prove that lines ![]() and
and ![]() are concurrent and the point of concurrence lies on
are concurrent and the point of concurrence lies on ![]()
Proof
Let ![]() and
and ![]() be the crosspoints of
be the crosspoints of ![]() with
with ![]() and
and ![]() respectively.
respectively.
WLOG ![]() Let
Let ![]() and
and ![]() be the points symmetric to
be the points symmetric to ![]() with respect
with respect ![]() and
and ![]() respectively.
respectively.
Therefore ![]()
![]()
![]()
Let ![]() be the crosspoint of
be the crosspoint of ![]() and
and ![]() is cyclic
is cyclic ![]()
Similarly ![]() is cyclic
is cyclic ![]() the crosspoint of
the crosspoint of ![]() and
and ![]() is point
is point ![]()
Usually the point ![]() is called the anti-Steiner point of the
is called the anti-Steiner point of the ![]() with respect to
with respect to ![]()
vladimir.shelomovskii@gmail.com, vvsss
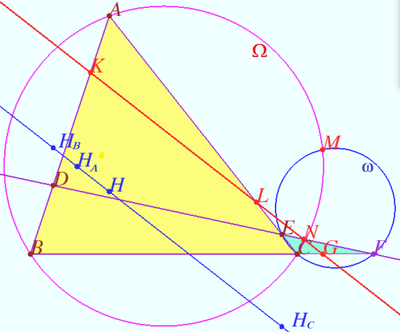
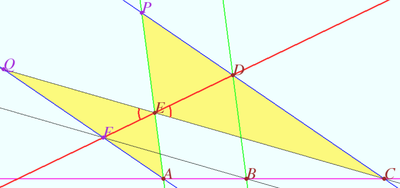
Ortholine
Let four lines made four triangles of a complete quadrilateral.
In the diagram these are ![]()
Let points ![]() and
and ![]() be the orthocenters of
be the orthocenters of ![]() and
and ![]() respectively.
respectively.
Prove that points ![]() and
and ![]() are collinear.
are collinear.
Proof
Let ![]() be Miquel point of a complete quadrilateral.
be Miquel point of a complete quadrilateral.
Line ![]() is the line which contain
is the line which contain ![]() Simson lines of
Simson lines of ![]() triangles.
triangles.
Using homothety centered at ![]() with ratio
with ratio ![]() we get
we get ![]() coinciding Stainer lines which contain points
coinciding Stainer lines which contain points ![]() and
and ![]() .
.
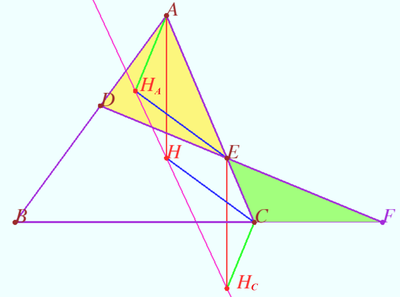
Proof 2
![]()
![]()
![]()
Points ![]() and
and ![]() are collinear.
are collinear.
According the Claim of parallel lines, points ![]() and
and ![]() are collinear.
are collinear.
Similarly points ![]() and
and ![]() are collinear as desired.
are collinear as desired.
Claim of parallel lines
Let points ![]() and
and ![]() be collinear.
be collinear.
Let points ![]() be such that
be such that ![]()
Prove that points ![]() and
and ![]() are collinear.
are collinear.
Proof
Let ![]()
![]()
![]()
![]()
![]()
The segments ![]() and
and ![]() are corresponding segments in similar triangles.
Therefore
are corresponding segments in similar triangles.
Therefore ![]() and
and ![]() are collinear.
are collinear.
vladimir.shelomovskii@gmail.com, vvsss
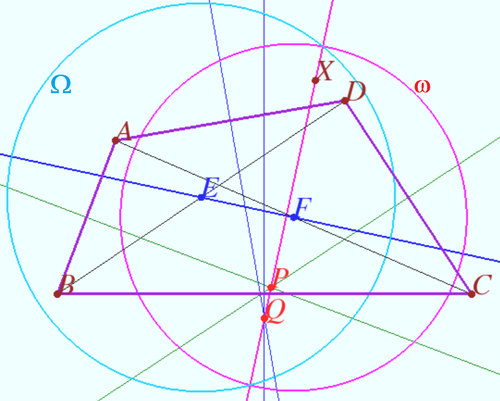
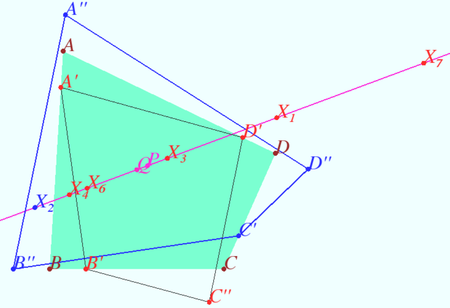
Shatunov-Tokarev line
Let the quadrilateral ![]() be given (
be given (![]() is not cyclic). Let points
is not cyclic). Let points ![]() and
and ![]() be the midpoints of
be the midpoints of ![]() and
and ![]() respectively. Let points
respectively. Let points ![]() and
and ![]() be such points that
be such points that ![]()
a) Prove that ![]()
b) Prove that the point ![]() lies on the line
lies on the line ![]() iff
iff ![]()
Proof
a) Let ![]() be the circle centered at
be the circle centered at ![]() with radius
with radius ![]() Let
Let ![]() be the circle centered at
be the circle centered at ![]() with radius
with radius ![]()
![]() is the median of
is the median of ![]()
The power of the point ![]() with respect to the circle
with respect to the circle ![]() is
is ![]()
![]() is the median of
is the median of ![]()
The power of the point ![]() with respect to the circle
with respect to the circle ![]() is
is ![]()
Therefore ![]() lies on the radical axis of
lies on the radical axis of ![]() and
and ![]() Similarly,
Similarly, ![]() lies on these line.
So the line
lies on these line.
So the line ![]() is the radical axes of
is the radical axes of ![]() and
and ![]()
This line is perpendicular to Gauss line ![]() which is the line of centers of two circles
which is the line of centers of two circles ![]() and
and ![]() as desired.
as desired.
b) ![]() is the median of
is the median of ![]()
![]() is the median of
is the median of ![]()
![]() lies on the radical axes of
lies on the radical axes of ![]() and
and ![]()
![]()
If the point ![]() satisfies the equation
satisfies the equation ![]() then locus of
then locus of ![]() is the straight line (one can prove it using method of coordinates).
is the straight line (one can prove it using method of coordinates).
The points ![]() and
and ![]() are satisfies this equation, so this line contain these points as desired.
are satisfies this equation, so this line contain these points as desired.
It is easy to understand that this line is parallel to Steiner line which is the radical axis of the circles centered at ![]() and
and ![]() with radii
with radii ![]() and
and ![]() respectively.
respectively.
Of course, it is parallel to Simson line.
vladimir.shelomovskii@gmail.com, vvsss
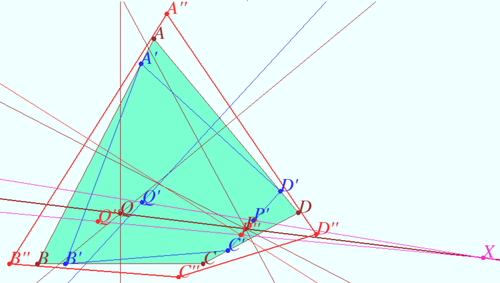
Shatunov-Tokarev concurrent lines
Let the quadrilateral ![]() be given (
be given (![]() is not cyclic).
is not cyclic).
Let points ![]() and
and ![]() be on the line
be on the line ![]() such that
such that ![]() . Similarly
. Similarly
![]()
![]()
![]()
Let points ![]() and
and ![]() be the crosspoints of the bisectors
be the crosspoints of the bisectors ![]()
Similarly points ![]() and
and ![]() are the crosspoints of the bisectors
are the crosspoints of the bisectors ![]()
Prove that lines ![]() and
and ![]() are concurrent.
are concurrent.
Proof
Segment ![]() is the median of the
is the median of the ![]()
Similarly ![]()
Let ![]() cross
cross ![]() at point
at point ![]()
We made simple calculations and get ![]() therefore point
therefore point ![]() lies on
lies on ![]() as desired.
vladimir.shelomovskii@gmail.com, vvsss
as desired.
vladimir.shelomovskii@gmail.com, vvsss
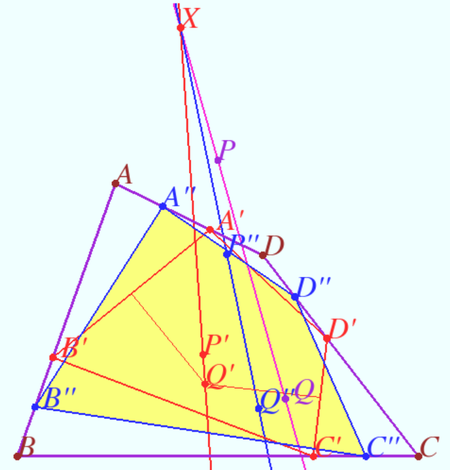
Shatunov point
Let the quadrilateral ![]() be given (
be given (![]() is not cyclic).
is not cyclic).
Let points ![]() and
and ![]() be on the lines
be on the lines ![]() and
and ![]() respectively such that
respectively such that ![]()
Let points ![]() and
and ![]() be on the segments
be on the segments ![]() and
and ![]() respectively such that
respectively such that ![]() where
where ![]()
Let points ![]() and
and ![]() be the crosspoints of the bisectors
be the crosspoints of the bisectors ![]()
Similarly points ![]() and
and ![]() are the crosspoints of the bisectors
are the crosspoints of the bisectors ![]()
Prove that lines ![]() and
and ![]() are concurrent.
are concurrent.
Proof
Segment ![]() is the cevian to the side AA' of the
is the cevian to the side AA' of the ![]()
We use the Stewart's theorem and get:
![]() Similarly
Similarly ![]()
![]()
![]() Let
Let ![]() cross
cross ![]() at point
at point ![]()
We made simple calculations and get ![]() therefore point
therefore point ![]() lies on
lies on ![]() as desired.
as desired.
vladimir.shelomovskii@gmail.com, vvsss
Shatunov chain
Let the quadrilateral ![]() be given (
be given (![]() is not cyclic).
is not cyclic).
Let points ![]() and
and ![]() be on the line
be on the line ![]() such that
such that ![]() . Similarly
. Similarly ![]()
![]()
Let points ![]() and
and ![]() be the crosspoints of the bisectors
be the crosspoints of the bisectors ![]() and
and ![]()
We made quadrilateral ![]() using one point from the pare
using one point from the pare ![]() one point from the pare
one point from the pare ![]() one point from the pare
one point from the pare ![]() one point from the pare
one point from the pare ![]() For each quadrilateral we find the crosspoints of the bisectors
For each quadrilateral we find the crosspoints of the bisectors ![]() and
and ![]() and named these points as
and named these points as ![]()
Prove that lines ![]() cross line
cross line ![]() in 8 points and positions of these points are fixed for given
in 8 points and positions of these points are fixed for given ![]() (not depend from the length of
(not depend from the length of ![]()
Proof
The claim follows from the fact that there are ![]() combinations of quadrilateral vertices, and these 16 quadrilaterals are divided into pairs whose points of intersection with the line
combinations of quadrilateral vertices, and these 16 quadrilaterals are divided into pairs whose points of intersection with the line ![]() coincide.
coincide.
vladimir.shelomovskii@gmail.com, vvsss