Difference between revisions of "Symmedians, Lemoine point"
(→Proportions) |
(→Proportions) |
||
| Line 35: | Line 35: | ||
Then <math>BE</math> is the <math>B-</math> symmedian of <math>\triangle ABD, CE</math> is the <math>C-</math> symmedian of <math>\triangle ACD, DE</math> is the <math>D-</math> symmedian of <math>\triangle BCD.</math> | Then <math>BE</math> is the <math>B-</math> symmedian of <math>\triangle ABD, CE</math> is the <math>C-</math> symmedian of <math>\triangle ACD, DE</math> is the <math>D-</math> symmedian of <math>\triangle BCD.</math> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | ==Symmedian and tangents== | ||
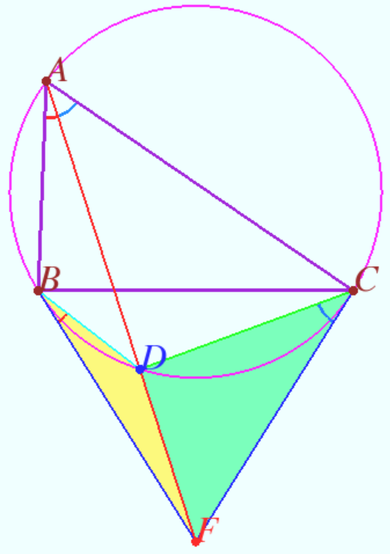
| + | [[File:Tangents and symmedian.png|390px|right]] | ||
| + | Let <math>\triangle ABC</math> and it’s circumcircle <math>\Omega</math> be given. Tangents to <math>\Omega</math> at points <math>B</math> and <math>C</math> intersect at point <math>F.</math> | ||
| + | Prove that <math>AF</math> is <math>A-</math> symmedian of <math>\triangle ABC.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Denote <math>D = AF \cap \Omega \ne A.</math> WLOG, <math>\angle BAC < 180^\circ.</math> | ||
| + | <cmath>\triangle FDB \sim \triangle FBA \implies \frac {BD}{AB} = \frac{DF}{BF}.</cmath> | ||
| + | <cmath>\triangle FDC \sim \triangle FCA \implies \frac {CD}{AC} = \frac{DF}{CF}.</cmath> | ||
| + | <math>BF = CF \implies \frac {BD}{CD} = \frac{AB}{AC} \implies AD</math> is <math>A-</math> symmedian of <math>\triangle ABC.</math> | ||
'''vladimir.shelomovskii@gmail.com, vvsss''' | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
Revision as of 14:03, 9 July 2024
The reflecting of the median over the corresponding angle bisector is the symmedian. The angle formed by the symmedian and the angle bisector has the same measure as the angle between the median and the angle bisector, but it is on the other side of the angle bisector. The symmedian ![]() is isogonally conjugate to the median
is isogonally conjugate to the median ![]()
There are three symmedians. They are meet at a triangle center called the Lemoine point.
Proportions
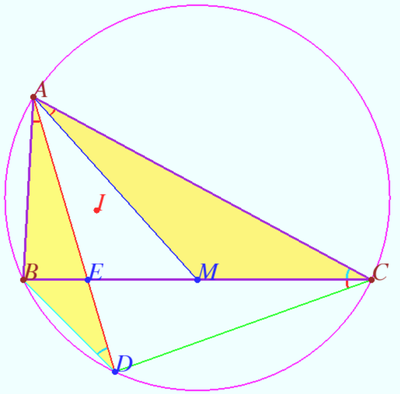
Let ![]() be given.
be given.
Let ![]() be the median,
be the median, ![]()
Prove that iff ![]() is the symmedian than
is the symmedian than ![]()
Proof
1. Let ![]() be the symmedian. So
be the symmedian. So ![]()
![]()
![]() Similarly
Similarly ![]()
![]()
By applying the Law of Sines we get
![]()
![]() Similarly,
Similarly, ![]()
2. ![]()
As point ![]() moves along the fixed arc
moves along the fixed arc ![]() from
from ![]() to
to ![]() , the function
, the function ![]() monotonically increases from zero to infinity. This means that there is exactly one point at which the condition is satisfied. In this case, point
monotonically increases from zero to infinity. This means that there is exactly one point at which the condition is satisfied. In this case, point ![]() lies on the symmedian.
lies on the symmedian.
Similarly for point ![]()
Corollary
Let ![]() be the
be the ![]() symmedian of
symmedian of ![]()
Then ![]() is the
is the ![]() symmedian of
symmedian of ![]() is the
is the ![]() symmedian of
symmedian of ![]() is the
is the ![]() symmedian of
symmedian of ![]()
vladimir.shelomovskii@gmail.com, vvsss
Symmedian and tangents
Let ![]() and it’s circumcircle
and it’s circumcircle ![]() be given. Tangents to
be given. Tangents to ![]() at points
at points ![]() and
and ![]() intersect at point
intersect at point ![]() Prove that
Prove that ![]() is
is ![]() symmedian of
symmedian of ![]()
Proof
Denote ![]() WLOG,
WLOG, ![]()
![]()
![]()
![]() is
is ![]() symmedian of
symmedian of ![]()
vladimir.shelomovskii@gmail.com, vvsss