Difference between revisions of "2007 AMC 10B Problems/Problem 21"
(Created page with "==Problem== Right <math>\triangle ABC</math> has <math>AB=3, BC=4,</math> and <math>AC=5.</math> Square <math>XYZW</math> is inscribed in <math>\triangle ABC</math> with <math>X...") |
m (→Solution 1) |
||
| (11 intermediate revisions by 9 users not shown) | |||
| Line 5: | Line 5: | ||
<math>\textbf{(A) } \frac{3}{2} \qquad\textbf{(B) } \frac{60}{37} \qquad\textbf{(C) } \frac{12}{7} \qquad\textbf{(D) } \frac{23}{13} \qquad\textbf{(E)} 2 </math> | <math>\textbf{(A) } \frac{3}{2} \qquad\textbf{(B) } \frac{60}{37} \qquad\textbf{(C) } \frac{12}{7} \qquad\textbf{(D) } \frac{23}{13} \qquad\textbf{(E)} 2 </math> | ||
| − | ==Solution== | + | ==Solution 1== |
[[Image:2007AMC10B21.png|center]] | [[Image:2007AMC10B21.png|center]] | ||
| − | There are | + | There are lots of similar triangles in the diagram, but we will only use <math>\triangle WBZ \sim \triangle ABC.</math> If <math>h</math> is the altitude from <math>B</math> to <math>AC</math> and <math>s</math> is the sidelength of the square, then <math>h-s</math> is the altitude from <math>B</math> to <math>WZ.</math> By similar triangles, |
<cmath>\begin{align*} | <cmath>\begin{align*} | ||
| − | \frac{h-s}{ | + | \frac{h-s}{h}&=\frac{s}{5}\ |
| + | 5(h-s)&=hs\ | ||
5h-5s&=hs\ | 5h-5s&=hs\ | ||
5h&=s(h+5)\ | 5h&=s(h+5)\ | ||
| Line 24: | Line 25: | ||
<cmath>s=\frac{5h}{h+5} = \frac{12}{7.4} = \boxed{\mathrm{(B) \ } \frac{60}{37}}</cmath> | <cmath>s=\frac{5h}{h+5} = \frac{12}{7.4} = \boxed{\mathrm{(B) \ } \frac{60}{37}}</cmath> | ||
| + | |||
| + | ==Solution 2== | ||
| + | |||
| + | Let <math>l</math> be the side length of the inscribed square. Note that <math>\triangle ZYC \sim \triangle WBZ \sim \triangle ABC</math>. | ||
| + | |||
| + | Then we can setup the following ratios: | ||
| + | |||
| + | <cmath>\frac{CZ}{l} = \frac{5}{3} \rightarrow CZ = \frac{5}{3}l</cmath> | ||
| + | <cmath>\frac{ZB}{l} = \frac{4}{5} \rightarrow ZB = \frac{4}{5}l</cmath> | ||
| + | |||
| + | But then <math>\frac{5}{3}l+\frac{4}{5}l = CZ+ZB = CB = 4 \longrightarrow \frac{37}{15}l=4 \longrightarrow l = \frac{60}{37} \Longrightarrow \boxed{\mathrm{(B)}\frac{60}{37}}</math> | ||
| + | |||
| + | == Video Solution by OmegaLearn== | ||
| + | https://youtu.be/FDgcLW4frg8?t=4662 | ||
| + | |||
| + | ~ pi_is_3.14 | ||
==See Also== | ==See Also== | ||
{{AMC10 box|year=2007|ab=B|num-b=20|num-a=22}} | {{AMC10 box|year=2007|ab=B|num-b=20|num-a=22}} | ||
| + | {{MAA Notice}} | ||
Latest revision as of 15:52, 29 July 2024
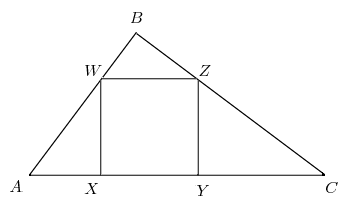
Problem
Right ![]() has
has ![]() and
and ![]() Square
Square ![]() is inscribed in
is inscribed in ![]() with
with ![]() and
and ![]() on
on ![]() on
on ![]() and
and ![]() on
on ![]() What is the side length of the square?
What is the side length of the square?
![]()
Solution 1
There are lots of similar triangles in the diagram, but we will only use ![]() If
If ![]() is the altitude from
is the altitude from ![]() to
to ![]() and
and ![]() is the sidelength of the square, then
is the sidelength of the square, then ![]() is the altitude from
is the altitude from ![]() to
to ![]() By similar triangles,
By similar triangles,

Find the length of the altitude of ![]() Since it is a right triangle, the area of
Since it is a right triangle, the area of ![]() is
is ![]()
The area can also be expressed as ![]() so
so ![]()
Substitute back into ![]()
![]()
Solution 2
Let ![]() be the side length of the inscribed square. Note that
be the side length of the inscribed square. Note that ![]() .
.
Then we can setup the following ratios:
![]()
![]()
But then ![]()
Video Solution by OmegaLearn
https://youtu.be/FDgcLW4frg8?t=4662
~ pi_is_3.14
See Also
| 2007 AMC 10B (Problems • Answer Key • Resources) | ||
| Preceded by Problem 20 |
Followed by Problem 22 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()