Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Surface of constant width"

(→‎Reuleaux triangle)
(→‎Reuleaux triangle analogue)
Line 28: Line 28:
  
 
The width of this curve is <cmath>|AB| + 2|AA'|.</cmath>
 
The width of this curve is <cmath>|AB| + 2|AA'|.</cmath>
 +
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
 +
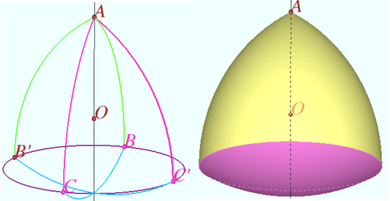
==Rotation of the Reuleaux triangle==
 +
[[File:Solid Reuleaux triangle rotation.png|390px|right]]
 +
The left part of diagram shows the curve <math>ABC</math> which is a Reuleaux triangle determined by the center <math>O</math> and the vertex <math>A.</math>
 +
 +
The Reuleaux triangle <math>AB'C'</math> is constructed by the rotation of the curve <math>ABC</math> around axis <math>AO.</math>
 +
 +
The right part of the diagram shows the surface which arose as the result of the rotation <math>ABC.</math>
  
 
'''vladimir.shelomovskii@gmail.com, vvsss'''
 
'''vladimir.shelomovskii@gmail.com, vvsss'''

Revision as of 07:39, 10 August 2024

A curve of constant width is a simple closed curve in the plane whose width (the distance between parallel supporting lines) is the same in all directions. A surface of constant width (orbiform) is a convex form whose width, measured by the distance between two opposite parallel planes touching its boundary, is the same regardless of the direction of those two parallel planes.

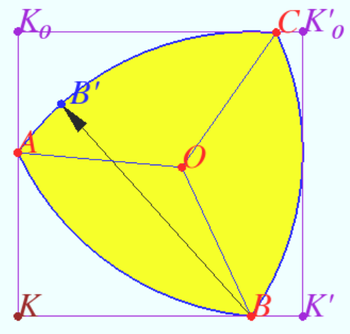
Reuleaux triangle

Reuleaux triangle.png

The boundary of a Reuleaux triangle is a constant width curve based on an equilateral triangle.

Let $\triangle ABC$ be equilateral triangle.

Let $\overset{\Large\frown} {AC}$ be the arc centered at $B$ with radius $BB' = BA, \angle ABC = 60^\circ.$

Arcs $\overset{\Large\frown} {AB}$ and $\overset{\Large\frown} {BC}$ define similarly.

All points on this arcs are equidistant from the opposite vertex.

Distance is $|AB|.$

vladimir.shelomovskii@gmail.com, vvsss

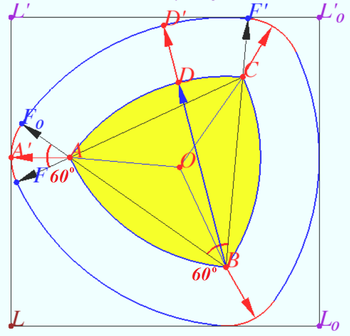
Reuleaux triangle analogue

Reuleaux triangle analogue.png

Let $ABCD$ be the boundary of a Reuleaux triangle, $O$ be the centroid of $\triangle ABC.$

Let $\overset{\Large\frown} {FF_0}$ be the arc centered at $A$ with radius $AA', \angle FAF_0 = 60^\circ,$ points $F, A, C$ and $F_0, A, B$ are collinear.

Let $\overset{\Large\frown} {F_0F'}$ be the arc centered at $B$ with radius \[|AA'| + |AB|,\] $\angle F'AF_0 = \angle ABC = 60^\circ,$ points $F', C, B$ are collinear.

Similarly define arcs from point $F'$ to $F.$

The width of this curve is \[|AB| + 2|AA'|.\]

vladimir.shelomovskii@gmail.com, vvsss

Rotation of the Reuleaux triangle

Solid Reuleaux triangle rotation.png

The left part of diagram shows the curve $ABC$ which is a Reuleaux triangle determined by the center $O$ and the vertex $A.$

The Reuleaux triangle $AB'C'$ is constructed by the rotation of the curve $ABC$ around axis $AO.$

The right part of the diagram shows the surface which arose as the result of the rotation $ABC.$

vladimir.shelomovskii@gmail.com, vvsss

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Surface_of_constant_width&oldid=224861"