Difference between revisions of "2003 AMC 10A Problems/Problem 22"
(→Lemma) |
(→Solution) |
||
| Line 8: | Line 8: | ||
== Solution == | == Solution == | ||
=== Solution 1 === | === Solution 1 === | ||
| + | <math>\angle GCH = \angle ABH</math> (Opposite angles are equal). | ||
| + | |||
| + | <math>\angle F = \angle B</math> (Both are 90 degrees). | ||
| + | |||
| + | <math>\angle BHA = \angle HAD</math> (Alt. Interior Angles are congruent). | ||
| + | |||
| + | Therefore <math>Triangles\: GFA</math> and <math>ABH</math> are similar. | ||
| + | <math>GCH</math> and <math>GEA</math> are also similar. | ||
| + | |||
| + | <math>DA</math> is 9, therefore <math>EA</math> must equal 5. Similarly, <math>CH</math> must equal 3. | ||
| + | |||
| + | Because <math>GCH</math> and <math>GEA</math> are similar, the ratio of <math>CH\; =\; 3</math> and <math>EA\; =\; 5</math>, must also hold true for <math>GH</math> and <math>HA</math>. <math>\frac{GH}{GA} = \frac{3}{5}</math>, so <math>HA</math> is <math>\frac{2}{5}</math> of <math>GA</math>. By Pythagorean theorem, <math>(HA)^2\; =\; (HB)^2\; +\; (BA)^2\;...\;HA=10</math>. | ||
| + | |||
| + | <math>HA\: =\: 10 =\: \frac{2}{5}*(GA)</math>. | ||
| + | |||
| + | <math>GA\: =\: 25.</math> | ||
| + | |||
| + | So <math>\frac{GA}{HA}\: =\: \frac{GF}{BA}</math>. | ||
| + | |||
| + | <math>\frac{25}{10}\: =\: \frac{GF}{8}</math>. | ||
| + | |||
| + | Therefore <math>GF\: = \boxed{20} = \boxed{\mathrm{(B)}}</math>. | ||
| + | |||
| + | === Solution 2 === | ||
Since <math>ABCD</math> is a rectangle, <math>CD=AB=8</math>. | Since <math>ABCD</math> is a rectangle, <math>CD=AB=8</math>. | ||
| Line 42: | Line 66: | ||
<math>GF=2 \cdot FD+8=2\cdot6+8=20 \Rightarrow B</math> | <math>GF=2 \cdot FD+8=2\cdot6+8=20 \Rightarrow B</math> | ||
| − | === Solution | + | === Solution 3 === |
Since <math>ABCD</math> is a rectangle, <math>CD=3</math>, <math>EA=5</math>, and <math>CD=8</math>. From the [[Pythagorean Theorem]], <math>CE^2=CD^2+DE^2=80\Rightarrow CE=4\sqrt{5}</math>. | Since <math>ABCD</math> is a rectangle, <math>CD=3</math>, <math>EA=5</math>, and <math>CD=8</math>. From the [[Pythagorean Theorem]], <math>CE^2=CD^2+DE^2=80\Rightarrow CE=4\sqrt{5}</math>. | ||
==== Lemma ==== | ==== Lemma ==== | ||
Revision as of 19:40, 15 February 2009
Contents
[hide]Problem
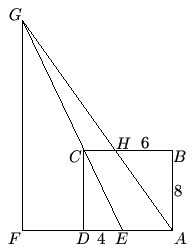
In rectangle ![]() , we have
, we have ![]() ,
, ![]() ,
, ![]() is on
is on ![]() with
with ![]() ,
, ![]() is on
is on ![]() with
with ![]() , line
, line ![]() intersects line
intersects line ![]() at
at ![]() , and
, and ![]() is on line
is on line ![]() with
with ![]() . Find the length of
. Find the length of ![]() .
.
![]()
Solution
Solution 1
![]() (Opposite angles are equal).
(Opposite angles are equal).
![]() (Both are 90 degrees).
(Both are 90 degrees).
![]() (Alt. Interior Angles are congruent).
(Alt. Interior Angles are congruent).
Therefore ![]() and
and ![]() are similar.
are similar.
![]() and
and ![]() are also similar.
are also similar.
![]() is 9, therefore
is 9, therefore ![]() must equal 5. Similarly,
must equal 5. Similarly, ![]() must equal 3.
must equal 3.
Because ![]() and
and ![]() are similar, the ratio of
are similar, the ratio of ![]() and
and ![]() , must also hold true for
, must also hold true for ![]() and
and ![]() .
. ![]() , so
, so ![]() is
is ![]() of
of ![]() . By Pythagorean theorem,
. By Pythagorean theorem, ![]() .
.
![]() .
.
![]()
So ![]() .
.
![]() .
.
Therefore ![]() .
.
Solution 2
Since ![]() is a rectangle,
is a rectangle, ![]() .
.
Since ![]() is a rectangle and
is a rectangle and ![]() ,
, ![]() .
.
Since ![]() is a rectangle,
is a rectangle, ![]() .
.
So, ![]() is a transversal, and
is a transversal, and ![]() .
.
This is sufficient to prove that ![]() and
and ![]() .
.
Using ratios:
![]()
![]()
![]()
![]()
![]()
![]()
Since ![]() can't have 2 different lengths, both expressions for
can't have 2 different lengths, both expressions for ![]() must be equal.
must be equal.
![]()
![]()
![]()
![]()
Solution 3
Since ![]() is a rectangle,
is a rectangle, ![]() ,
, ![]() , and
, and ![]() . From the Pythagorean Theorem,
. From the Pythagorean Theorem, ![]() .
.
Lemma
Statement: ![]()
Proof: ![]() , obviously.
, obviously.
$
Since two angles of the triangles are equal, the third angles must equal each other. Therefore, the triangles are similar.
Let ![]() .
.

Also, ![]() , therefore
, therefore
![]()
We can multiply both sides by ![]() to get that
to get that ![]() is twice of 10, or
is twice of 10, or ![]()
See Also
| 2003 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 21 |
Followed by Problem 23 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||