Difference between revisions of "1977 Canadian MO Problems"
m (→Problem 7) |
(→Problem 7) |
||
| Line 52: | Line 52: | ||
to work each day but, on any given trip, she makes sure that her path does not include any intersection | to work each day but, on any given trip, she makes sure that her path does not include any intersection | ||
twice. Show that the number <math>f(m,n)</math> of different paths she can take to work satisfies <math>f(m,n)\le 2^{mn}</math>. | twice. Show that the number <math>f(m,n)</math> of different paths she can take to work satisfies <math>f(m,n)\le 2^{mn}</math>. | ||
| + | |||
| + | <math>\begin{tabular}{|c|c|c|c|c|c|c|c|c|c|c| } | ||
| + | \hline | ||
| + | &&&&&&&&&& \\ \hline | ||
| + | &&&&&&&&&& \\ \hline | ||
| + | &&&&&&&&&& \\ \hline | ||
| + | &&&&&&&&&& \\ \hline | ||
| + | &&&&&&&&&& \\ \hline | ||
| + | &&&&&&&&&& \\ \hline | ||
| + | &&&&&&&&&& \\ \hline | ||
| + | \end{tabular}</math> | ||
[[1977 Canadian MO Problems/Problem 7 | Solution]] | [[1977 Canadian MO Problems/Problem 7 | Solution]] | ||
Revision as of 01:17, 7 October 2014
The seven problems were all on the same day.
Contents
Problem 1
If 
prove that the equation 
has no solutions in positive integers 
and 
Problem 2
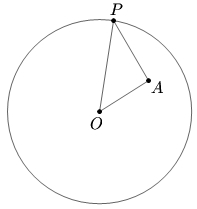
Let 
be the center of a circle and 
be a fixed interior point of the circle different from 
Determine all points 
on the circumference of the circle such that the angle 
is a maximum.
Problem 3
is an integer whose representation in base 
is 
Find the smallest positive integer for which is the fourth power of an integer.
Problem 4
Let
![\[p(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots +a_1x+a_0\]](http://latex.artofproblemsolving.com/c/1/2/c126ff597ee283022b1c7295806fabde784acccf.png)
and
![\[q(x)=b_mx^m+b_{m-1}x^{m-1}+\cdots +b_1x+b_0\]](http://latex.artofproblemsolving.com/d/f/a/dfabcbca27ad4f78679b62c9b3a5618cc10354f9.png)
be two polynomials with integer coefficients. Suppose that all of the coefficients of the product 
are even, but not all of them are divisible by 4. Show that one of 
and 
has all even coefficients
and the other has at least one odd coefficient.
Problem 5
Problem 6
Let 
and define
![\[u_1=1+u\quad ,\quad u_2=\frac{1}{u_1}+u\quad \ldots\quad u_{n+1}=\frac{1}{u_n}+u\quad ,\quad n\ge 1\]](http://latex.artofproblemsolving.com/6/0/a/60abc54bcbc1505553158b221308b91482b30cb9.png)
Show that 
for all values of 
.
Problem 7
A rectangular city is exactly 
blocks long and 
blocks wide (see diagram).
A woman lives on the southwest corner of the city and works in the northeast corner. She walks
to work each day but, on any given trip, she makes sure that her path does not include any intersection
twice. Show that the number 
of different paths she can take to work satisfies 
.
