Difference between revisions of "2003 AMC 12A Problems/Problem 17"
m (→Solution 1) |
Drkotlovmath (talk | contribs) (→Solution 3) |
||
| Line 45: | Line 45: | ||
Pythagorean theorem gives us <math>AM=2 \sqrt{5}</math>. Clearly <math>\triangle XMD \sim \triangle XDA \sim \triangle DMA \sim \triangle ZDP</math> by angle-angle and <math>\triangle XMD \cong \triangle XMP</math> by Hypotenuse Leg. | Pythagorean theorem gives us <math>AM=2 \sqrt{5}</math>. Clearly <math>\triangle XMD \sim \triangle XDA \sim \triangle DMA \sim \triangle ZDP</math> by angle-angle and <math>\triangle XMD \cong \triangle XMP</math> by Hypotenuse Leg. | ||
Manipulating similar triangles gives us <math>PZ=\frac{16}{5}</math> | Manipulating similar triangles gives us <math>PZ=\frac{16}{5}</math> | ||
| + | |||
| + | ==Solution 4== | ||
| + | Using the double-angle formula for sine, what we need to find is <math>AD\cdot \sin(DAP) = AD\cdot 2\sin( DAM) \cos(DAM) = 4\cdot 2\cdot \frac{2}{\sqrt{20}}\cdot\frac{4}{\sqrt{20}} = \frac{16}{5}</math>. | ||
== See Also == | == See Also == | ||
Revision as of 20:39, 10 February 2015
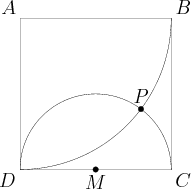
Problem
Square ![]() has sides of length
has sides of length ![]() , and
, and ![]() is the midpoint of
is the midpoint of ![]() . A circle with radius
. A circle with radius ![]() and center
and center ![]() intersects a circle with radius
intersects a circle with radius ![]() and center
and center ![]() at points
at points ![]() and
and ![]() . What is the distance from
. What is the distance from ![]() to
to ![]() ?
?
![]()
Solution 1
Let ![]() be the origin.
be the origin. ![]() is the point
is the point ![]() and
and ![]() is the point
is the point ![]() . We are given the radius of the quarter circle and semicircle as
. We are given the radius of the quarter circle and semicircle as ![]() and
and ![]() , respectively, so their equations, respectively, are:
, respectively, so their equations, respectively, are:
![]()
![]()
Subtract the second equation from the first:
![]()
![]()
![]()
Then substitute:
![]()
![]()
![]()
![]()
Thus ![]() and
and ![]() making
making ![]() and
and ![]() .
.
The first value of ![]() is obviously referring to the x-coordinate of the point where the circles intersect at the origin,
is obviously referring to the x-coordinate of the point where the circles intersect at the origin, ![]() , so the second value must be referring to the x coordinate of
, so the second value must be referring to the x coordinate of ![]() . Since
. Since ![]() is the y-axis, the distance to it from
is the y-axis, the distance to it from ![]() is the same as the x-value of the coordinate of
is the same as the x-value of the coordinate of ![]() , so the distance from
, so the distance from ![]() to
to ![]() is
is ![]()
Solution 2
Note that ![]() is merely a reflection of
is merely a reflection of ![]() over
over ![]() . Call the intersection of
. Call the intersection of ![]() and
and ![]()
![]() . Drop perpendiculars from
. Drop perpendiculars from ![]() and
and ![]() to
to ![]() , and denote their respective points of intersection by
, and denote their respective points of intersection by ![]() and
and ![]() . We then have
. We then have ![]() , with a scale factor of 2. Thus, we can find
, with a scale factor of 2. Thus, we can find ![]() and double it to get our answer. With some analytical geometry, we find that
and double it to get our answer. With some analytical geometry, we find that ![]() , implying that
, implying that ![]() .
.
Solution 3
As in Solution 2, draw in ![]() and
and ![]() and denote their intersection point
and denote their intersection point ![]() . Next, drop a perpendicular from
. Next, drop a perpendicular from ![]() to
to ![]() and denote the foot as
and denote the foot as ![]() .
. ![]() as they are both radii and similarly
as they are both radii and similarly ![]() so
so ![]() is a kite and
is a kite and ![]() by a well-known theorem.
by a well-known theorem.
Pythagorean theorem gives us ![]() . Clearly
. Clearly ![]() by angle-angle and
by angle-angle and ![]() by Hypotenuse Leg.
Manipulating similar triangles gives us
by Hypotenuse Leg.
Manipulating similar triangles gives us ![]()
Solution 4
Using the double-angle formula for sine, what we need to find is ![]() .
.
See Also
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()