Difference between revisions of "2017 AMC 12A Problems/Problem 16"
Toffeecube (talk | contribs) |
Toffeecube (talk | contribs) (→Problem) |
||
| Line 3: | Line 3: | ||
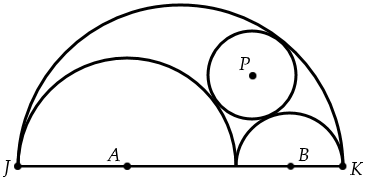
In the figure below, semicircles with centers at <math>A</math> and <math>B</math> and with radii 2 and 1, respectively, are drawn in the interior of, and sharing bases with, a semicircle with diameter <math>JK</math>. The two smaller semicircles are externally tangent to each other and internally tangent to the largest semicircle. A circle centered at <math>P</math> is drawn externally tangent to the two smaller semicircles and internally tangent to the largest semicircle. What is the radius of the circle centered at <math>P</math>? | In the figure below, semicircles with centers at <math>A</math> and <math>B</math> and with radii 2 and 1, respectively, are drawn in the interior of, and sharing bases with, a semicircle with diameter <math>JK</math>. The two smaller semicircles are externally tangent to each other and internally tangent to the largest semicircle. A circle centered at <math>P</math> is drawn externally tangent to the two smaller semicircles and internally tangent to the largest semicircle. What is the radius of the circle centered at <math>P</math>? | ||
| − | [[File:2017amc12a16.png| | + | [[File:2017amc12a16.png|2017amc12a16.png]] |
<math> \textbf{(A)}\ 3/4 | <math> \textbf{(A)}\ 3/4 | ||
Revision as of 17:46, 8 February 2017
Problem
In the figure below, semicircles with centers at 
and 
and with radii 2 and 1, respectively, are drawn in the interior of, and sharing bases with, a semicircle with diameter 
. The two smaller semicircles are externally tangent to each other and internally tangent to the largest semicircle. A circle centered at 
is drawn externally tangent to the two smaller semicircles and internally tangent to the largest semicircle. What is the radius of the circle centered at ?
