Difference between revisions of "Mock AIME 2 2006-2007 Problems/Problem 14"
(→Problem) |
|||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
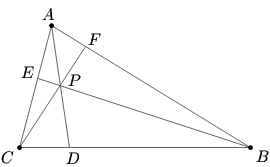
| − | In triangle ABC, <math>\displaystyle AB = 308</math> and <math>\displaystyle AC=35.</math> Given that <math>\displaystyle AD</math>, <math>\displaystyle BE,</math> and <math>\displaystyle CF,</math> intersect at <math>\displaystyle P</math> and are an angle bisector, median, and altitude of the triangle, respectively, compute the length of <math>\displaystyle BC.</math> | + | In triangle ABC, <math>\displaystyle AB = 308</math> and <math>\displaystyle AC=35.</math> Given that <math>\displaystyle AD</math>, <math>\displaystyle BE,</math> and <math>\displaystyle CF,</math> intersect at <math>\displaystyle P</math> and are an angle bisector, median, and altitude of the triangle, respectively, compute the length of <math>\displaystyle BC.</math> |
| + | |||
| + | [[Image:Mock AIME 2 2007 Problem14.jpg]] | ||
== Problem Source == | == Problem Source == | ||
4everwise thought of this problem after reading the first chapter of Geometry Revisited. | 4everwise thought of this problem after reading the first chapter of Geometry Revisited. | ||
Revision as of 23:08, 24 July 2006
Problem
In triangle ABC, 
and 
Given that 
, 
and 
intersect at 
and are an angle bisector, median, and altitude of the triangle, respectively, compute the length of 
Problem Source
4everwise thought of this problem after reading the first chapter of Geometry Revisited.
