Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Mock AIME 2 2006-2007 Problems"

(→‎Problem 6)
(→‎Problem 7)
 
(7 intermediate revisions by 3 users not shown)
Line 1: Line 1:
 
== Problem 1 ==
 
== Problem 1 ==
−
A positive integer is called a dragon if it can be [[partitioned]] into four positive integers <math>\displaystyle a,b,c,</math> and <math>\displaystyle d</math> such that <math>\displaystyle a+4=b-4=4c=d/4.</math> Find the smallest dragon.
+
A positive integer is called a ''dragon'' if it can be written as the sum of four positive integers <math>a,b,c,</math> and <math>d</math> such that <math>a+4=b-4=4c=d/4.</math> Find the smallest dragon.
  
−
[[Mock_AIME_2_2006-2007/Problem_1|Solution]]
+
[[Mock_AIME_2_2006-2007 Problems/Problem_1|Solution]]
  
 
== Problem 2 ==
 
== Problem 2 ==
−
The set <math>\displaystyle S</math> consists of all integers from <math>\displaystyle 1</math> to <math>\displaystyle 2007,</math> inclusive. For how many elements <math>\displaystyle n</math> in <math>\displaystyle S</math> is <math>\displaystyle f(n) = \frac{2n^3+n^2-n-2}{n^2-1}</math> an integer?
+
The set <math>S</math> consists of all integers from <math>1</math> to <math>2007,</math> inclusive. For how many elements <math>n</math> in <math>S</math> is <math>f(n) = \frac{2n^3+n^2-n-2}{n^2-1}</math> an integer?
  
−
[[Mock_AIME_2_2006-2007/Problem_2|Solution]]
+
[[Mock_AIME_2_2006-2007 Problems/Problem_2|Solution]]
  
 
== Problem 3 ==
 
== Problem 3 ==
−
Let <math>\displaystyle S</math> be the sum of all positive integers <math>\displaystyle n</math> such that <math>\displaystyle n^2+12n-2007</math> is a perfect square. Find the remainder when <math>\displaystyle S</math> is divided by <math>\displaystyle 1000.</math>
+
Let <math>S</math> be the sum of all positive integers <math>n</math> such that <math>n^2+12n-2007</math> is a perfect square. Find the remainder when <math>S</math> is divided by <math>1000.</math>
  
−
[[Mock_AIME_2_2006-2007/Problem_3|Solution]]
+
[[Mock_AIME_2_2006-2007 Problems/Problem_3|Solution]]
  
 
== Problem 4 ==
 
== Problem 4 ==
−
Let <math>\displaystyle n</math> be the smallest positive integer for which there exist positive real numbers <math>\displaystyle a</math> and <math>\displaystyle b</math> such that <math>\displaystyle (a+bi)^n=(a-bi)^n</math>. Compute <math>\displaystyle \frac{b^2}{a^2}</math>.
+
Let <math>n</math> be the smallest positive integer for which there exist positive real numbers <math>a</math> and <math>b</math> such that <math>(a+bi)^n=(a-bi)^n</math>. Compute <math>\frac{b^2}{a^2}</math>.
  
−
[[Mock_AIME_2_2006-2007/Problem_4|Solution]]
+
[[Mock_AIME_2_2006-2007 Problems/Problem_4|Solution]]
  
 
== Problem 5 ==
 
== Problem 5 ==
−
Given that <math>\displaystyle  iz^2=1+\frac 2z + \frac{3}{z^2}+\frac{4}{z ^3}+\frac{5}{z^4}+\cdots</math> and <math>\displaystyle z=a\pm \sqrt{b+i},</math> find <math>\displaystyle  \lfloor 100ab \rfloor.</math>
+
Given that <math> iz^2=1+\frac 2z + \frac{3}{z^2}+\frac{4}{z ^3}+\frac{5}{z^4}+\cdots</math> and <math>z=n\pm \sqrt{-i},</math> find <math> \lfloor 100n \rfloor.</math>
  
−
[[Mock_AIME_2_2006-2007/Problem_5|Solution]]
+
[[Mock_AIME_2_2006-2007 Problems/Problem_5|Solution]]
  
 
== Problem 6 ==
 
== Problem 6 ==
−
If <math>\displaystyle \tan 15^\circ \tan 25^\circ \tan 35^\circ =\tan \theta</math> and <math>\displaystyle 0^\circ \le \theta \le 180^\circ, </math> find <math>\displaystyle \theta.</math>
+
If <math>\tan 15^\circ \tan 25^\circ \tan 35^\circ =\tan \theta</math> and <math>0^\circ \le \theta \le 180^\circ, </math> find <math>\theta.</math>
  
−
[[Mock_AIME_2_2006-2007/Problem_6|Solution]]
+
[[Mock_AIME_2_2006-2007 Problems/Problem_6|Solution]]
  
 
== Problem 7 ==
 
== Problem 7 ==
−
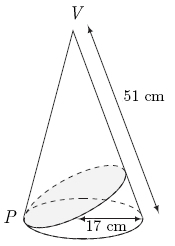
A right circular cone of base radius <math>\displaystyle 17</math>cm and slant height <math>\displaystyle 34</math>cm is given. <math>\displaystyle P</math> is a point on the circumference of the base and the shortest path from <math>\displaystyle P</math> around the cone and back is drawn (see diagram). If the minimum distance from the vertex <math>\displaystyle V</math> to this path is <math>\displaystyle m\sqrt{n},</math> where <math>\displaystyle m</math> and <math>\displaystyle n</math> are relatively prime positive integers, find <math>\displaystyle m+n.</math>  
+
A right circular cone of base radius <math>17</math>cm and slant height <math>51</math>cm is given. <math>P</math> is a point on the circumference of the base and the shortest path from <math>P</math> around the cone and back is drawn (see diagram). If the length of this path is <math>m\sqrt{n},</math> where <math>m</math> and <math>n</math> are relatively prime positive integers, find <math>m+n.</math>
  
−
[[Image:Mock_AIME_2_2007_Problem7.jpg]]
+
[[Image:Mock_AIME_2_2007_Problem8.jpg]]
  
−
[[Mock_AIME_2_2006-2007/Problem_7|Solution]]
+
[[Mock_AIME_2_2006-2007 Problems/Problem_7|Solution]]
  
 
== Problem 8 ==
 
== Problem 8 ==
−
The positive integers <math>\displaystyle x_1, x_2, ... , x_7</math> satisfy <math>\displaystyle x_6 = 144</math> and <math>\displaystyle x_{n+3} = x_{n+2}(x_{n+1}+x_n)</math> for <math>\displaystyle n = 1, 2, 3, 4</math>. Find the last three digits of <math>\displaystyle x_7</math>.
+
The positive integers <math>x_1, x_2, ... , x_7</math> satisfy <math>x_6 = 144</math> and <math>x_{n+3} = x_{n+2}(x_{n+1}+x_n)</math> for <math>n = 1, 2, 3, 4</math>. Find the last three digits of <math>x_7</math>.
  
−
[[Mock_AIME_2_2006-2007/Problem_8|Solution]]
+
[[Mock_AIME_2_2006-2007 Problems/Problem_8|Solution]]
  
 
== Problem 9 ==
 
== Problem 9 ==
−
In right triangle <math>\displaystyle ABC,</math> <math>\displaystyle \angle C=90^\circ.</math> Cevians <math>\displaystyle AX</math> and <math>\displaystyle BY</math> are drawn to <math>\displaystyle BC</math> and <math>\displaystyle AC</math> respectively such that <math>\displaystyle \frac{BX}{CX}=\frac23</math> and <math>\displaystyle \frac{AY}{CY}=\sqrt 3.</math> If <math>\displaystyle \tan \angle APB= \frac{a+b\sqrt{c}}{d},</math> where <math>\displaystyle a,b,</math> and <math>\displaystyle d</math> are relatively prime and <math>\displaystyle c</math> has no perfect square divisors excluding <math>\displaystyle 1,</math> find <math>\displaystyle a+b+c+d.</math>
+
In right triangle <math>ABC,</math> <math>\angle C=90^\circ.</math> Cevians <math>AX</math> and <math>BY</math> intersect at <math>P</math> and are drawn to <math>BC</math> and <math>AC</math> respectively such that <math>\frac{BX}{CX}=\frac23</math> and <math>\frac{AY}{CY}=\sqrt 3.</math> If <math>\tan \angle APB= \frac{a+b\sqrt{c}}{d},</math> where <math>a,b,</math> and <math>d</math> are relatively prime and <math>c</math> has no perfect square divisors excluding <math>1,</math> find <math>a+b+c+d.</math>
  
−
[[Mock_AIME_2_2006-2007/Problem_9|Solution]]
+
[[Mock_AIME_2_2006-2007 Problems/Problem_9|Solution]]
  
 
== Problem 10 ==
 
== Problem 10 ==
−
Find the number of solutions, in degrees, to the equation <math>\displaystyle \sin^{10}x + \cos^{10}x = \frac{29}{16}\cos^4 2x,</math> where <math>\displaystyle 0^\circ \le x^\circ \le 2007^\circ.</math>
+
Find the number of solutions, in degrees, to the equation <math>\sin^{10}x + \cos^{10}x = \frac{29}{16}\cos^4 2x,</math> where <math>0^\circ \le x^\circ \le 2007^\circ.</math>
  
−
[[Mock_AIME_2_2006-2007/Problem_10|Solution]]
+
[[Mock_AIME_2_2006-2007 Problems/Problem_10|Solution]]
  
 
== Problem 11 ==
 
== Problem 11 ==
 
Find the sum of the squares of the roots, real or complex, of the system of simultaneous equations
 
Find the sum of the squares of the roots, real or complex, of the system of simultaneous equations
  
−
<math>\displaystyle x+y+z=3,~x^2+y^2+z^2=3,~x^3+y^3+z^3 =3.</math>
+
<math>x+y+z=3,~x^2+y^2+z^2=3,~x^3+y^3+z^3 =3.</math>
  
−
[[Mock_AIME_2_2006-2007/Problem_11|Solution]]
+
[[Mock_AIME_2_2006-2007 Problems/Problem_11|Solution]]
  
 
== Problem 12 ==
 
== Problem 12 ==
−
In quadrilateral <math>\displaystyle ABCD,</math> <math>\displaystyle m \angle DAC= m\angle DBC </math> and <math>\displaystyle \frac{[ADB]}{[ABC]}=\frac12.</math> If <math>\displaystyle AD=4,</math> <math>\displaystyle BC=6</math>, <math>\displaystyle BO=1,</math> and the area of <math>\displaystyle ABCD</math> is <math>\displaystyle \frac{a\sqrt{b}}{c},</math> where <math>\displaystyle a,b,c</math> are relatively prime positive integers, find <math>\displaystyle a+b+c.</math>
+
In quadrilateral <math>ABCD,</math> <math>m \angle DAC= m\angle DBC </math> and <math>\frac{[ADB]}{[ABC]}=\frac12.</math> If <math>AD=4,</math> <math>BC=6</math>, <math>BO=1,</math> and the area of <math>ABCD</math> is <math>\frac{a\sqrt{b}}{c},</math> where <math>a,b,c</math> are relatively prime positive integers, find <math>a+b+c.</math>
  
  
−
Note*: <math>\displaystyle[ABC]</math> and <math>\displaystyle[ADB]</math> refer to the areas of triangles <math>\displaystyle ABC</math> and <math>\displaystyle ADB.</math>
+
Note*: <math>[ABC]</math> and <math>[ADB]</math> refer to the areas of triangles <math>ABC</math> and <math>ADB.</math>
  
−
[[Mock_AIME_2_2006-2007/Problem_12|Solution]]
+
[[Mock_AIME_2_2006-2007 Problems/Problem_12|Solution]]
  
 
== Problem 13 ==
 
== Problem 13 ==
−
In his spare time, Richard Rusczyk shuffles a standard deck of 52 playing cards. He then turns the cards up one by one from the top of the deck until the third ace appears. If the expected (average) number of cards Richard will turn up is <math>\displaystyle m/n,</math> where <math>\displaystyle m</math> and <math>\displaystyle n</math> are relatively prime positive integers, find <math>\displaystyle m+n.</math>
+
In his spare time, Richard Rusczyk shuffles a standard deck of 52 playing cards. He then turns the cards up one by one from the top of the deck until the third ace appears. If the expected (average) number of cards Richard will turn up is <math>m/n,</math> where <math>m</math> and <math>n</math> are relatively prime positive integers, find <math>m+n.</math>
  
−
[[Mock_AIME_2_2006-2007/Problem_13|Solution]]
+
[[Mock_AIME_2_2006-2007 Problems/Problem_13|Solution]]
  
 
== Problem 14 ==
 
== Problem 14 ==
  
−
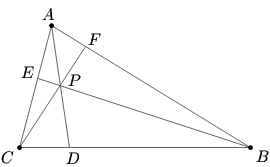
In triangle ABC, <math>\displaystyle AB = 308</math> and <math>\displaystyle AC=35.</math> Given that <math>\displaystyle AD</math>, <math>\displaystyle BE,</math> and <math>\displaystyle CF,</math> intersect at <math>\displaystyle P</math> and are an angle bisector, median, and altitude of the triangle, respectively, compute the length of <math>\displaystyle BC.</math>
+
In triangle ABC, <math>AB = 308</math> and <math>AC=35.</math> Given that <math>AD</math>, <math>BE,</math> and <math>CF,</math> intersect at <math>P</math> and are an angle bisector, median, and altitude of the triangle, respectively, compute the length of <math>BC.</math>
  
 
[[Image:Mock AIME 2 2007 Problem14.jpg]]
 
[[Image:Mock AIME 2 2007 Problem14.jpg]]
  
−
[[Mock_AIME_2_2006-2007/Problem_14|Solution]]
+
[[Mock_AIME_2_2006-2007 Problems/Problem_14|Solution]]
  
 
== Problem 15 ==
 
== Problem 15 ==
  
−
A <math>\displaystyle 4\times4\times4</math> cube is composed of <math>\displaystyle 64</math> unit cubes. The faces of <math>\displaystyle 16</math> unit cubes are colored red. An arrangement of the cubes is <math>\mathfrak{Intriguing}</math> if there is exactly <math>\displaystyle 1</math> red unit cube in every <math>\displaystyle 1\times1\times4</math> rectangular box composed of <math>\displaystyle 4</math> unit cubes. Determine the number of <math>\mathfrak{Intriguing}</math> colorings.
+
A <math>4\times4\times4</math> cube is composed of <math>64</math> unit cubes. The faces of <math>16</math> unit cubes are colored red. An arrangement of the cubes is <math>\mathfrak{Intriguing}</math> if there is exactly <math>1</math> red unit cube in every <math>1\times1\times4</math> rectangular box composed of <math>4</math> unit cubes. Determine the number of <math>\mathfrak{Intriguing}</math> colorings.
  
−
[[Mock_AIME_2_2006-2007/Problem_15|Solution]]
+
[[Mock_AIME_2_2006-2007 Problems/Problem_15|Solution]]
  
 
[[Image:CubeArt.jpg]]
 
[[Image:CubeArt.jpg]]

Latest revision as of 22:49, 25 February 2017

Problem 1

A positive integer is called a dragon if it can be written as the sum of four positive integers $a,b,c,$ and $d$ such that $a+4=b-4=4c=d/4.$ Find the smallest dragon.

Solution

Problem 2

The set $S$ consists of all integers from $1$ to $2007,$ inclusive. For how many elements $n$ in $S$ is $f(n) = \frac{2n^3+n^2-n-2}{n^2-1}$ an integer?

Solution

Problem 3

Let $S$ be the sum of all positive integers $n$ such that $n^2+12n-2007$ is a perfect square. Find the remainder when $S$ is divided by $1000.$

Solution

Problem 4

Let $n$ be the smallest positive integer for which there exist positive real numbers $a$ and $b$ such that $(a+bi)^n=(a-bi)^n$. Compute $\frac{b^2}{a^2}$.

Solution

Problem 5

Given that $iz^2=1+\frac 2z + \frac{3}{z^2}+\frac{4}{z ^3}+\frac{5}{z^4}+\cdots$ and $z=n\pm \sqrt{-i},$ find $\lfloor 100n \rfloor.$

Solution

Problem 6

If $\tan 15^\circ \tan 25^\circ \tan 35^\circ =\tan \theta$ and $0^\circ \le \theta \le 180^\circ,$ find $\theta.$

Solution

Problem 7

A right circular cone of base radius $17$cm and slant height $51$cm is given. $P$ is a point on the circumference of the base and the shortest path from $P$ around the cone and back is drawn (see diagram). If the length of this path is $m\sqrt{n},$ where $m$ and $n$ are relatively prime positive integers, find $m+n.$

Mock AIME 2 2007 Problem8.jpg

Solution

Problem 8

The positive integers $x_1, x_2, ... , x_7$ satisfy $x_6 = 144$ and $x_{n+3} = x_{n+2}(x_{n+1}+x_n)$ for $n = 1, 2, 3, 4$. Find the last three digits of $x_7$.

Solution

Problem 9

In right triangle $ABC,$ $\angle C=90^\circ.$ Cevians $AX$ and $BY$ intersect at $P$ and are drawn to $BC$ and $AC$ respectively such that $\frac{BX}{CX}=\frac23$ and $\frac{AY}{CY}=\sqrt 3.$ If $\tan \angle APB= \frac{a+b\sqrt{c}}{d},$ where $a,b,$ and $d$ are relatively prime and $c$ has no perfect square divisors excluding $1,$ find $a+b+c+d.$

Solution

Problem 10

Find the number of solutions, in degrees, to the equation $\sin^{10}x + \cos^{10}x = \frac{29}{16}\cos^4 2x,$ where $0^\circ \le x^\circ \le 2007^\circ.$

Solution

Problem 11

Find the sum of the squares of the roots, real or complex, of the system of simultaneous equations

$x+y+z=3,~x^2+y^2+z^2=3,~x^3+y^3+z^3 =3.$

Solution

Problem 12

In quadrilateral $ABCD,$ $m \angle DAC= m\angle DBC$ and $\frac{[ADB]}{[ABC]}=\frac12.$ If $AD=4,$ $BC=6$, $BO=1,$ and the area of $ABCD$ is $\frac{a\sqrt{b}}{c},$ where $a,b,c$ are relatively prime positive integers, find $a+b+c.$


Note*: $[ABC]$ and $[ADB]$ refer to the areas of triangles $ABC$ and $ADB.$

Solution

Problem 13

In his spare time, Richard Rusczyk shuffles a standard deck of 52 playing cards. He then turns the cards up one by one from the top of the deck until the third ace appears. If the expected (average) number of cards Richard will turn up is $m/n,$ where $m$ and $n$ are relatively prime positive integers, find $m+n.$

Solution

Problem 14

In triangle ABC, $AB = 308$ and $AC=35.$ Given that $AD$, $BE,$ and $CF,$ intersect at $P$ and are an angle bisector, median, and altitude of the triangle, respectively, compute the length of $BC.$

Mock AIME 2 2007 Problem14.jpg

Solution

Problem 15

A $4\times4\times4$ cube is composed of $64$ unit cubes. The faces of $16$ unit cubes are colored red. An arrangement of the cubes is $\mathfrak{Intriguing}$ if there is exactly $1$ red unit cube in every $1\times1\times4$ rectangular box composed of $4$ unit cubes. Determine the number of $\mathfrak{Intriguing}$ colorings.

Solution

CubeArt.jpg

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Mock_AIME_2_2006-2007_Problems&oldid=84208"