Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2021 AIME I Problems/Problem 6"

m (Changed the title of the solutions.)
m
 
(22 intermediate revisions by 11 users not shown)
Line 1: Line 1:
 
==Problem==
 
==Problem==
−
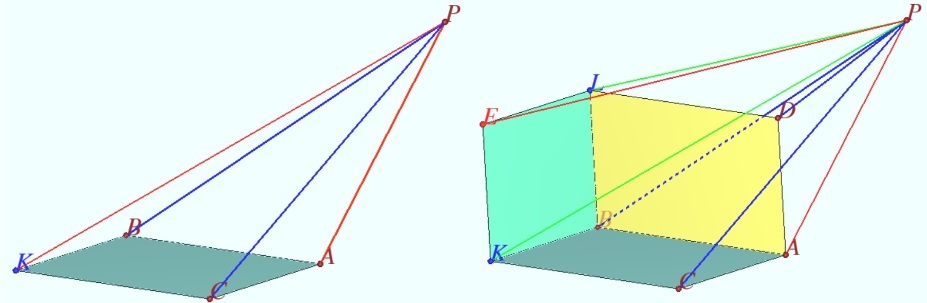
Segments <math>\overline{AB}, \overline{AC},</math> and <math>\overline{AD}</math> are edges of a cube and <math>\overline{AG}</math> is a diagonal through the center of the cube. Point <math>P</math> satisfies <math>PB=60\sqrt{10}, PC=60\sqrt{5}, PD=120\sqrt{2},</math> and <math>PG=36\sqrt{7}</math>. What is <math>PA</math>?
+
Segments <math>\overline{AB}, \overline{AC},</math> and <math>\overline{AD}</math> are edges of a cube and <math>\overline{AG}</math> is a diagonal through the center of the cube. Point <math>P</math> satisfies <math>BP=60\sqrt{10}</math>, <math>CP=60\sqrt{5}</math>, <math>DP=120\sqrt{2}</math>, and <math>GP=36\sqrt{7}</math>. Find <math>AP.</math>
  
 
==Solution 1==
 
==Solution 1==
−
First scale down the whole cube by 12. Let point P have coordinates <math>(x, y, z)</math>, A have coordinates <math>(0, 0, 0)</math>, and <math>s</math> be the side length. Then we have the equations
+
First scale down the whole cube by <math>12</math>. Let point <math>P</math> have coordinates <math>(x, y, z)</math>, point <math>A</math> have coordinates <math>(0, 0, 0)</math>, and <math>s</math> be the side length. Then we have the equations
−
<cmath>(s-x)^2+y^2+z^2=(5\sqrt{10})^2</cmath>
+
<cmath>\begin{align*}
−
<cmath>x^2+(s-y)^2+z^2=(5\sqrt{5})^2</cmath>
+
(s-x)^2+y^2+z^2&=\left(5\sqrt{10}\right)^2, \\
−
<cmath>x^2+y^2+(s-z)^2=(10\sqrt{2})^2</cmath>
+
x^2+(s-y)^2+z^2&=\left(5\sqrt{5}\right)^2, \\
−
<cmath>(s-x)^2+(s-y)^2+(s-z)^2=(3\sqrt{7})^2</cmath>
+
x^2+y^2+(s-z)^2&=\left(10\sqrt{2}\right)^2, \\
 +
(s-x)^2+(s-y)^2+(s-z)^2&=\left(3\sqrt{7}\right)^2.
 +
\end{align*}</cmath>
 
These simplify into
 
These simplify into
−
<cmath>s^2+x^2+y^2+z^2-2sx=250</cmath>
+
<cmath>\begin{align*}
−
<cmath>s^2+x^2+y^2+z^2-2sy=125</cmath>
+
s^2+x^2+y^2+z^2-2sx&=250, \\
−
<cmath>s^2+x^2+y^2+z^2-2sz=200</cmath>
+
s^2+x^2+y^2+z^2-2sy&=125, \\
−
<cmath>3s^2-2s(x+y+z)+x^2+y^2+z^2=63</cmath>
+
s^2+x^2+y^2+z^2-2sz&=200, \\
 +
3s^2-2s(x+y+z)+x^2+y^2+z^2&=63.
 +
\end{align*}</cmath>
 
Adding the first three equations together, we get <math>3s^2-2s(x+y+z)+3(x^2+y^2+z^2)=575</math>.
 
Adding the first three equations together, we get <math>3s^2-2s(x+y+z)+3(x^2+y^2+z^2)=575</math>.
−
Subtracting these, we get <math>2(x^2+y^2+z^2)=512</math>, so <math>x^2+y^2+z^2=256</math>. This means <math>PA=16</math>. However, we scaled down everything by 12 so our answer is <math>16*12=\boxed{192}</math>.
+
Subtracting this from the fourth equation, we get <math>2(x^2+y^2+z^2)=512</math>, so <math>x^2+y^2+z^2=256</math>. This means <math>PA=16</math>. However, we scaled down everything by <math>12</math> so our answer is <math>16*12=\boxed{192}</math>.
 +
 
 
~JHawk0224
 
~JHawk0224
  
−
==Solution 2 (Solution 1 with slight simplification)==
+
==Solution 2 (Solution 1 with Slight Simplification)==
−
Once the equations for the distance between point P and the vertices of the cube have been written. We can add the first, second, and third to receive, <cmath>2(x^2 + y^2 + z^2) + (s-x)^2 + (s-y)^2 + (s-z)^2 = 250 + 125 + 200.</cmath> Subtracting the fourth equation gives, <cmath>2(x^2 + y^2 + z^2) = 575 - 63</cmath> <cmath>x^2 + y^2 + z^2 = 256</cmath> <cmath>\sqrt{x^2 + y^2 + z^2} = 16.</cmath> Since point <math>A = (0,0,0), PA = 16</math>, and since we scaled the answer is <math>16 \cdot 12 = \boxed{192}</math>
+
Once the equations for the distance between point P and the vertices of the cube have been written, we can add the first, second, and third to receive, <cmath>2(x^2 + y^2 + z^2) + (s-x)^2 + (s-y)^2 + (s-z)^2 = 250 + 125 + 200.</cmath> Subtracting the fourth equation gives
 +
<cmath>\begin{align*}
 +
2(x^2 + y^2 + z^2) &= 575 - 63 \\
 +
x^2 + y^2 + z^2 &= 256 \\
 +
\sqrt{x^2 + y^2 + z^2} &= 16.
 +
\end{align*}</cmath>
 +
Since point <math>A = (0,0,0), PA = 16</math>, and since we scaled the answer is <math>16 \cdot 12 = \boxed{192}</math>.
 +
 
 
~Aaryabhatta1
 
~Aaryabhatta1
−
==See also==
+
 
 +
==Solution 3==
 +
 
 +
Let <math>E</math> be the vertex of the cube such that <math>ABED</math> is a square.
 +
Using the [[British Flag Theorem]], we can easily show that
 +
<cmath>PA^2 + PE^2 = PB^2 + PD^2</cmath>
 +
and
 +
<cmath>PA^2 + PG^2 = PC^2 + PE^2</cmath>
 +
Hence, by adding the two equations together, we get <math>2PA^2 + PG^2 = PB^2 + PC^2 + PD^2</math>. Substituting in the values we know, we get <math>2PA^2 + 7\cdot 36^2 =10\cdot60^2 + 5\cdot 60^2 + 2\cdot 120^2 </math>.
 +
 
 +
Thus, we can solve for <math>PA</math>, which ends up being <math>\boxed{192}</math>.
 +
 
 +
(Lokman GÖKÇE)
 +
[[File:2021 AIME I 6b.jpg|size:100px]]
 +
 
 +
==Solution 4==
 +
For all points <math>X</math> in space, define the function <math>f:\mathbb{R}^{3}\rightarrow\mathbb{R}</math> by <math>f(X)=PX^{2}-GX^{2}</math>. Then <math>f</math> is linear; let <math>O=\frac{2A+G}{3}</math> be the center of <math>\triangle BCD</math>. Then since <math>f</math> is linear,
 +
<cmath>\begin{align*}
 +
3f(O)=f(B)+f(C)+f(D)&=2f(A)+f(G) \\
 +
\left(PB^{2}-GB^{2}\right)+\left(PC^{2}-GC^{2}\right)+\left(PD^{2}-GD^{2}\right)&=2\left(PA^{2}-GA^{2}\right)+PG^{2} \\
 +
\left(60\sqrt{10}\right)^{2}-2x^{2}+\left(60\sqrt{5}\right)^{2}-2x^{2}+\left(120\sqrt{2}\right)^{2}-2x^{2}&=2PA^{2}-2\cdot 3x^{2}+\left(36\sqrt{7}\right)^{2},
 +
\end{align*}</cmath>
 +
where <math>x</math> denotes the side length of the cube. Thus
 +
<cmath>\begin{align*}
 +
36\text{,}000+18\text{,}000+28\text{,}800-6x^{2}&=2PA^{2}-6x^{2}+9072 \\
 +
82\text{,}800-6x^{2}&=2PA^{2}-6x^{2}+9072 \\
 +
73\text{,}728&=2PA^{2} \\
 +
36\text{,}864&=PA^{2} \\
 +
PA&=\boxed{192}.
 +
\end{align*}</cmath>
 +
 
 +
 
 +
==See Also==
 
{{AIME box|year=2021|n=I|num-b=5|num-a=7}}
 
{{AIME box|year=2021|n=I|num-b=5|num-a=7}}
  

Latest revision as of 23:50, 11 January 2024

Problem

Segments $\overline{AB}, \overline{AC},$ and $\overline{AD}$ are edges of a cube and $\overline{AG}$ is a diagonal through the center of the cube. Point $P$ satisfies $BP=60\sqrt{10}$, $CP=60\sqrt{5}$, $DP=120\sqrt{2}$, and $GP=36\sqrt{7}$. Find $AP.$

Solution 1

First scale down the whole cube by $12$. Let point $P$ have coordinates $(x, y, z)$, point $A$ have coordinates $(0, 0, 0)$, and $s$ be the side length. Then we have the equations \begin{align*} (s-x)^2+y^2+z^2&=\left(5\sqrt{10}\right)^2, \\ x^2+(s-y)^2+z^2&=\left(5\sqrt{5}\right)^2, \\ x^2+y^2+(s-z)^2&=\left(10\sqrt{2}\right)^2, \\ (s-x)^2+(s-y)^2+(s-z)^2&=\left(3\sqrt{7}\right)^2. \end{align*} These simplify into \begin{align*} s^2+x^2+y^2+z^2-2sx&=250, \\ s^2+x^2+y^2+z^2-2sy&=125, \\ s^2+x^2+y^2+z^2-2sz&=200, \\ 3s^2-2s(x+y+z)+x^2+y^2+z^2&=63. \end{align*} Adding the first three equations together, we get $3s^2-2s(x+y+z)+3(x^2+y^2+z^2)=575$. Subtracting this from the fourth equation, we get $2(x^2+y^2+z^2)=512$, so $x^2+y^2+z^2=256$. This means $PA=16$. However, we scaled down everything by $12$ so our answer is $16*12=\boxed{192}$.

~JHawk0224

Solution 2 (Solution 1 with Slight Simplification)

Once the equations for the distance between point P and the vertices of the cube have been written, we can add the first, second, and third to receive, \[2(x^2 + y^2 + z^2) + (s-x)^2 + (s-y)^2 + (s-z)^2 = 250 + 125 + 200.\] Subtracting the fourth equation gives \begin{align*} 2(x^2 + y^2 + z^2) &= 575 - 63 \\ x^2 + y^2 + z^2 &= 256 \\ \sqrt{x^2 + y^2 + z^2} &= 16. \end{align*} Since point $A = (0,0,0), PA = 16$, and since we scaled the answer is $16 \cdot 12 = \boxed{192}$.

~Aaryabhatta1

Solution 3

Let $E$ be the vertex of the cube such that $ABED$ is a square. Using the British Flag Theorem, we can easily show that \[PA^2 + PE^2 = PB^2 + PD^2\] and \[PA^2 + PG^2 = PC^2 + PE^2\] Hence, by adding the two equations together, we get $2PA^2 + PG^2 = PB^2 + PC^2 + PD^2$. Substituting in the values we know, we get $2PA^2 + 7\cdot 36^2 =10\cdot60^2 + 5\cdot 60^2 + 2\cdot 120^2$.

Thus, we can solve for $PA$, which ends up being $\boxed{192}$.

(Lokman GÖKÇE) size:100px

Solution 4

For all points $X$ in space, define the function $f:\mathbb{R}^{3}\rightarrow\mathbb{R}$ by $f(X)=PX^{2}-GX^{2}$. Then $f$ is linear; let $O=\frac{2A+G}{3}$ be the center of $\triangle BCD$. Then since $f$ is linear, \begin{align*} 3f(O)=f(B)+f(C)+f(D)&=2f(A)+f(G) \\ \left(PB^{2}-GB^{2}\right)+\left(PC^{2}-GC^{2}\right)+\left(PD^{2}-GD^{2}\right)&=2\left(PA^{2}-GA^{2}\right)+PG^{2} \\ \left(60\sqrt{10}\right)^{2}-2x^{2}+\left(60\sqrt{5}\right)^{2}-2x^{2}+\left(120\sqrt{2}\right)^{2}-2x^{2}&=2PA^{2}-2\cdot 3x^{2}+\left(36\sqrt{7}\right)^{2}, \end{align*} where $x$ denotes the side length of the cube. Thus \begin{align*} 36\text{,}000+18\text{,}000+28\text{,}800-6x^{2}&=2PA^{2}-6x^{2}+9072 \\ 82\text{,}800-6x^{2}&=2PA^{2}-6x^{2}+9072 \\ 73\text{,}728&=2PA^{2} \\ 36\text{,}864&=PA^{2} \\ PA&=\boxed{192}. \end{align*}


See Also

2021 AIME I (Problems • Answer Key • Resources)
Preceded by
Problem 5 		Followed by
Problem 7
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2021_AIME_I_Problems/Problem_6&oldid=210511"