Difference between revisions of "2021 JMPSC Sprint Problems/Problem 13"
| (One intermediate revision by the same user not shown) | |||
| Line 12: | Line 12: | ||
== Solution 2== | == Solution 2== | ||
The diameter is <math>15</math>. Therefore, | The diameter is <math>15</math>. Therefore, | ||
| − | <cmath>\pi \left(\frac{15}{2}\right)^2 \cdot 8=450 \pi</cmath> | + | <cmath>\pi \left(\frac{15}{2}\right)^2 \cdot 8=450 \pi</cmath> So, <math>k=\boxed{450}</math> |
| + | |||
| + | - kante314 - | ||
==See also== | ==See also== | ||
Latest revision as of 09:47, 12 July 2021
Contents
Problem
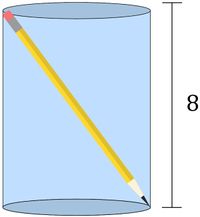
Grace places a pencil in a cylindrical cup and is surprised to see that it fits diagonally. The pencil is 
units long and of negligible thickness. The cup is 
units tall. The volume of the cup can be written as 
cubic units. Find 
.
Solution
By the Pythagorean Theorem, we have that the diameter of the cylinder's base is 15 units long. Thus, the cylinder's base has radius 
units. Thus, the volume of the cylinder is 
~Lamboreghini
Solution 2
The diameter is 
. Therefore,
![\[\pi \left(\frac{15}{2}\right)^2 \cdot 8=450 \pi\]](http://latex.artofproblemsolving.com/5/4/0/5403ac5c013c1c9e3f5820dc1759e292d1e7e919.png)
So, 
- kante314 -
See also
The problems on this page are copyrighted by the Junior Mathematicians' Problem Solving Competition. 
