Difference between revisions of "2021 Fall AMC 10B Problems/Problem 18"
(→Solution 3 (30-60-90 Triangles)) |
Xhypotenuse (talk | contribs) |
||
| (128 intermediate revisions by 14 users not shown) | |||
| Line 1: | Line 1: | ||
==Problem== | ==Problem== | ||
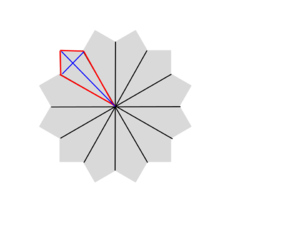
Three identical square sheets of paper each with side length <math>6{ }</math> are stacked on top of each other. The middle sheet is rotated clockwise <math>30^\circ</math> about its center and the top sheet is rotated clockwise <math>60^\circ</math> about its center, resulting in the <math>24</math>-sided polygon shown in the figure below. The area of this polygon can be expressed in the form <math>a-b\sqrt{c}</math>, where <math>a</math>, <math>b</math>, and <math>c</math> are positive integers, and <math>c</math> is not divisible by the square of any prime. What is <math>a+b+c?</math> | Three identical square sheets of paper each with side length <math>6{ }</math> are stacked on top of each other. The middle sheet is rotated clockwise <math>30^\circ</math> about its center and the top sheet is rotated clockwise <math>60^\circ</math> about its center, resulting in the <math>24</math>-sided polygon shown in the figure below. The area of this polygon can be expressed in the form <math>a-b\sqrt{c}</math>, where <math>a</math>, <math>b</math>, and <math>c</math> are positive integers, and <math>c</math> is not divisible by the square of any prime. What is <math>a+b+c?</math> | ||
| + | <center><asy> | ||
| + | defaultpen(fontsize(8)+0.8); size(150); | ||
| + | pair O,A1,B1,C1,A2,B2,C2,A3,B3,C3,A4,B4,C4; | ||
| + | real x=45, y=90, z=60; O=origin; | ||
| + | A1=dir(x); A2=dir(x+y); A3=dir(x+2y); A4=dir(x+3y); | ||
| + | B1=dir(x-z); B2=dir(x+y-z); B3=dir(x+2y-z); B4=dir(x+3y-z); | ||
| + | C1=dir(x-2z); C2=dir(x+y-2z); C3=dir(x+2y-2z); C4=dir(x+3y-2z); | ||
| + | draw(A1--A2--A3--A4--A1, gray+0.25+dashed); | ||
| + | filldraw(B1--B2--B3--B4--cycle, white, gray+dashed+linewidth(0.25)); | ||
| + | filldraw(C1--C2--C3--C4--cycle, white, gray+dashed+linewidth(0.25)); | ||
| + | dot(O); | ||
| + | pair P1,P2,P3,P4,Q1,Q2,Q3,Q4,R1,R2,R3,R4; | ||
| + | P1=extension(A1,A2,B1,B2); Q1=extension(A1,A2,C3,C4); | ||
| + | P2=extension(A2,A3,B2,B3); Q2=extension(A2,A3,C4,C1); | ||
| + | P3=extension(A3,A4,B3,B4); Q3=extension(A3,A4,C1,C2); | ||
| + | P4=extension(A4,A1,B4,B1); Q4=extension(A4,A1,C2,C3); | ||
| + | R1=extension(C2,C3,B2,B3); R2=extension(C3,C4,B3,B4); | ||
| + | R3=extension(C4,C1,B4,B1); R4=extension(C1,C2,B1,B2); | ||
| + | draw(A1--P1--B2--R1--C3--Q1--A2); | ||
| + | draw(A2--P2--B3--R2--C4--Q2--A3); | ||
| + | draw(A3--P3--B4--R3--C1--Q3--A4); | ||
| + | draw(A4--P4--B1--R4--C2--Q4--A1); | ||
| + | </asy></center> | ||
| + | <math>(\textbf{A})\: 75\qquad(\textbf{B}) \: 93\qquad(\textbf{C}) \: 96\qquad(\textbf{D}) \: 129\qquad(\textbf{E}) \: 147</math> | ||
| + | |||
| + | |||
| + | ==Solution 1== | ||
| + | <asy> | ||
| + | defaultpen(fontsize(8)+0.8); size(100); | ||
| + | pair A=(0,0); | ||
| + | pair B=(1.732,3); | ||
| + | pair C=(3,3); | ||
| + | pair D=(3,1.732); | ||
| + | draw(A--(0,3)--C--(3,0)--A, lightgray+dashed); | ||
| + | draw(A--B--C--A); | ||
| + | draw(A--D--C, gray); | ||
| + | label("$A$",A,W); | ||
| + | label("$B$",B,N); | ||
| + | label("$C$",C,NE); | ||
| + | label("$D$",D,E); | ||
| + | label("$E$",(0,3),NW); | ||
| + | label("$F$",(3,0),E); | ||
| + | </asy> | ||
| + | The <math>24</math>-sided polygon is made out of <math>24</math> shapes like <math>\triangle ABC</math>. Then <math>\angle BAC=360^\circ/24=15^\circ</math>, and <math>\angle EAC = 45^\circ</math>, so <math>\angle{EAB} = 30^{\circ}</math>. Then <math>EB=AE\tan 30^\circ = \sqrt{3}</math>; therefore <math>BC=EC-EB=3-\sqrt{3}</math>. Thus | ||
| + | <cmath>[ABC] = \frac{BC}{EC}\cdot [ACE] = \frac{3-\sqrt{3}}{3}\cdot \frac 92 </cmath>and the required area is <math>24\cdot[ABC] =108-36\sqrt{3}</math>. Finally <math>108+36+3=\boxed{(\textbf{E})\ 147}</math>. | ||
| + | ~lopkiloinm | ||
| + | |||
| − | <math>(\ | + | ==Solution 2 (15-75-90 triangles)== |
| + | <center><asy> | ||
| + | defaultpen(fontsize(8)+0.8); size(150); | ||
| + | pair O,A1,B1,C1,A2,B2,C2,A3,B3,C3,A4,B4,C4; | ||
| + | real x=45, y=90, z=60; O=origin; | ||
| + | A1=dir(x); A2=dir(x+y); A3=dir(x+2y); A4=dir(x+3y); | ||
| + | B1=dir(x-z); B2=dir(x+y-z); B3=dir(x+2y-z); B4=dir(x+3y-z); | ||
| + | C1=dir(x-2z); C2=dir(x+y-2z); C3=dir(x+2y-2z); C4=dir(x+3y-2z); | ||
| + | draw(A1--A2--A3--A4--A1, gray+0.25+dashed); | ||
| + | filldraw(B1--B2--B3--B4--cycle, white, gray+dashed+linewidth(0.25)); | ||
| + | filldraw(C1--C2--C3--C4--cycle, white, gray+dashed+linewidth(0.25)); | ||
| + | filldraw(O--C3--B2--cycle, white, black+linewidth(0.5)); | ||
| + | dot(O); | ||
| + | label("$O$",O,W); | ||
| + | label("$B$",C3,N); | ||
| + | label("$C$",B2,N); | ||
| + | label("$A$",(0,0.8),S); | ||
| + | pair P1,P2,P3,P4,Q1,Q2,Q3,Q4,R1,R2,R3,R4; | ||
| + | P1=extension(A1,A2,B1,B2); Q1=extension(A1,A2,C3,C4); | ||
| + | P2=extension(A2,A3,B2,B3); Q2=extension(A2,A3,C4,C1); | ||
| + | P3=extension(A3,A4,B3,B4); Q3=extension(A3,A4,C1,C2); | ||
| + | P4=extension(A4,A1,B4,B1); Q4=extension(A4,A1,C2,C3); | ||
| + | R1=extension(C2,C3,B2,B3); R2=extension(C3,C4,B3,B4); | ||
| + | R3=extension(C4,C1,B4,B1); R4=extension(C1,C2,B1,B2); | ||
| + | draw(A1--P1--B2--R1--C3--Q1--A2); | ||
| + | draw(A2--P2--B3--R2--C4--Q2--A3); | ||
| + | draw(A3--P3--B4--R3--C1--Q3--A4); | ||
| + | draw(A4--P4--B1--R4--C2--Q4--A1); | ||
| + | </asy></center> | ||
| + | |||
| + | |||
| + | |||
| + | |||
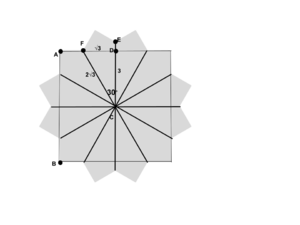
| + | Break the <math>24</math>-gon as shown so that there are <math>12</math> copies of quadrilateral <math>OBAC</math>. We can find the area of this quadrilateral by finding the area of triangle <math>OBC</math> and subtracting the area of triangle <math>ABC</math>. | ||
| + | |||
| + | The angle from <math>O</math> to one of the vertices of the original square is <math>45^\circ{}</math>, and this point rotates <math>30^\circ{}</math>, so the angle that <math>OC</math> makes with the horizontal is <math>75^\circ{}</math>. | ||
| + | |||
| + | Let <math>D</math> be the intersection of <math>OA</math> with <math>BC</math>. Since <math>ABC</math> and <math>OBC</math> are both isosceles, <math>OD</math> forms a right angle with <math>BC</math>. Furthermore, <math>\angle DOC = 90^\circ{}-75^\circ{} = 15^\circ{}</math>. | ||
| + | |||
| + | <center><asy> | ||
| + | import olympiad; | ||
| + | pair O,C,D; | ||
| + | D=(0,4); | ||
| + | O=(0,0); | ||
| + | C=(1.1,4); | ||
| + | draw(O--C--D--cycle); | ||
| + | label("$D$",D,N); | ||
| + | label("$C$",C,N); | ||
| + | label("$O$",O,S); | ||
| + | path angle = anglemark(C, O, D); | ||
| + | draw(rightanglemark(O, D, C)); | ||
| + | </asy></center> | ||
| + | |||
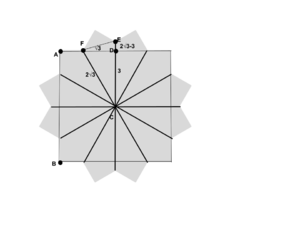
| + | Note that <math>OC</math> is equal to <math>3\sqrt{2}</math> because it is half the diagonal of the square with side length <math>6</math>. We can now split up the <math>15-75-90</math> into <math>30-60-90</math> and <math>15-15-150</math> triangles to find the height and length of the triangle: | ||
| + | |||
| + | <center><asy> | ||
| + | import olympiad; | ||
| + | pair O,C,D,E; | ||
| + | D=(0,4); | ||
| + | O=(0,0); | ||
| + | C=(1.1,4); | ||
| + | E=(0,2.1); | ||
| + | draw(O--C--D--cycle); | ||
| + | label("$D$",D,N); | ||
| + | label("$C$",C,N); | ||
| + | label("$O$",O,S); | ||
| + | label("$3\sqrt{2}$",(1.3,2),E); | ||
| + | path angle = anglemark(C, O, D); | ||
| + | draw(rightanglemark(O, D, C)); | ||
| + | draw(C--E); | ||
| + | label("$E$",E,W); | ||
| + | label("$x$",(0.5,4),N); | ||
| + | label("$x\sqrt{3}$",(-0.1,3.2),W); | ||
| + | label("$2x$",(-0.1,1),W); | ||
| + | |||
| + | </asy></center> | ||
| + | |||
| + | Now we have use Pythagorean: <math>x^2+(x \cdot (2+\sqrt{3}))^2 = 3\sqrt{2}^2 \implies x^2+x^2 \cdot (7+4\sqrt{3}) = 18</math> | ||
| + | <math> \implies x^2 = \frac{18}{8+4\sqrt{3}} = \frac{9}{4+2\sqrt{3}} \implies x^2 = \frac{36-18\sqrt{3}}{4}</math> | ||
| + | |||
| + | Now note that <math>x</math> must be in the form of <math>\frac{a\sqrt{3}-b}{2}</math>. Therefore, <math>-2ab = -18 \implies ab=9</math>. We can guess that <math>a=b=3</math>. Sure enough, <math>3\sqrt{3}^2 +3^2= 36</math>, so <math>x = \frac{3\sqrt{3}-3}{2}</math>. Then the height of the triangle is <math>x \cdot (2+\sqrt{3}) = \frac{3\sqrt{3}+3}{2}</math>. | ||
| + | |||
| + | The area of triangle <math>OBC</math> is equal to the length times the height of triangle <math>ODC</math> since this triangle has half the area of the full triangle. Therefore the area of triangle <math>OBC = \frac{3\sqrt{3}-3}{2} \cdot \frac{3\sqrt{3}+3}{2} = \frac{18}{4}</math>. | ||
| + | |||
| + | Now we look at triangle <math>ABC</math>. <math>\angle OCA = 45^\circ{}</math> because <math>OC</math> is the diagonal of a square, and <math>\angle COA</math> is <math>15^\circ{}</math> as we saw earlier. Therefore, <math>\angle OAC = \angle OAB = 120^\circ{}</math>. Because both these angles are <math>120</math>, <math>\angle BAC = 360-240 = 120</math>. | ||
| + | |||
| + | We can now split triangle <math>ABC</math> into two congruent <math>30-60-90</math> triangles, and we know the base of each since <math>BC = 3\sqrt{3}-3</math>. | ||
| + | |||
| + | The height of these triangles is <math>\frac{\frac{3\sqrt{3}-3}{2}}{\sqrt{3}} = \frac{3-\sqrt{3}}{2}</math>. Therefore the area of this triangle is <math>\frac{3\sqrt{3}-3}{2} \cdot \frac{3-\sqrt{3}}{2} = \frac{12\sqrt{3}-18}{4}</math> | ||
| + | |||
| + | Therefore the total area of this segment is <math>\frac{18}{4}-(\frac{12\sqrt{3}-18}{4}) = \frac{36-12\sqrt{3}}{4} = 9-3\sqrt{3}</math>. Multiplying by <math>12</math> to find the entire area, the area of the figure is <math>108-36\sqrt{3}</math> and the answer is <math>108+36+3 = 147 = \boxed{E}</math> | ||
| + | |||
| + | |||
| + | |||
| + | ~KingRavi | ||
| + | |||
| + | ==Solution 3== | ||
| + | First note the useful fact that if <math>R</math> is the circumradius of a dodecagon (<math>12</math>-gon) the area of the figure is <math>3R^2.</math> If we connect the vertices of the <math>3</math> squares we get a dodecagon. The radius of circumcircle of the dodecagon is simply half the diagonal of the square, which is <math>3\sqrt{2}.</math> Thus the area of the dodecagon is <math>3 \cdot (3\sqrt{2})^2 = 3 \cdot 18 = 54.</math> But, the problem asked for the area of the combined figure which was made from the rotated squares. This area is the area of the dodecagon, which was found, subtracting the <math>12</math> isosceles triangles, which are formed when connecting the vertices of the squares to created the dodecagon. To find this area, we need to know the base of the isosceles triangle, call this <math>x.</math> Then, we can use the Law of Cosines on the triangle that is formed from the two vertices of the square and the center of the square. After computing, we get that <math>x = 3\sqrt{3} -3.</math> Realize that the <math>12</math> isosceles are congruent with an angle measure of <math>120^{\circ},</math> this means that we can create <math>4</math> congruent equilateral triangles with side length of <math>3\sqrt3 - 3.</math> The area of the equilateral triangle is <math>\frac{\sqrt{3}}{4} \cdot (3\sqrt{3} -3)^2 = \frac{\sqrt{3}}{4} \cdot (36 - 18\sqrt{3}) = \frac{36\sqrt{3} - 54}{4}.</math> Thus, the area of all the twelve small equilateral traingles are <math>4 \cdot \frac{36\sqrt{3} - 54}{4} = 36\sqrt{3} - 54</math>. Thus, the requested area is <math>54 - (36\sqrt{3} - 54) = 108 - 36\sqrt{3}.</math> Thus, <math>a+b+c = 108 + 36 + 3 = 147,</math> so the answer is <math>\boxed{(\textbf{E})\textbf{147}}.</math> | ||
| + | |||
| + | ~NH14 | ||
| + | |||
| + | ==Solution 4 (30-60-90 Triangles)== | ||
| + | |||
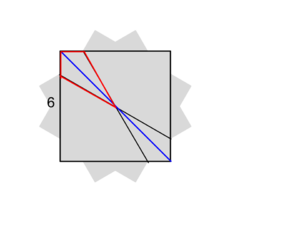
| + | To make things simpler, let's take only the original sheet and the 30 degree rotated sheet. Then the diagram is this; | ||
| + | |||
| + | <asy> | ||
| + | |||
| + | size(10cm,0); | ||
| + | path p = box((0,0), (1,1)); | ||
| + | draw(p, black + linewidth(2.0pt)); | ||
| + | draw(rotate(30,(1/2,1/2))*p,black + linewidth(2.0pt)); /*Rotate 60 | ||
| + | degrees*/ | ||
| + | |||
| + | </asy> | ||
| + | |||
| + | The area of this diagram is the original square plus the area of the four triangles that 'jut' out of the square. Because the square is rotated <math>30^{\circ}</math>, each triangle is a 30-60-90 triangle. Similarly, the triangles that are bounded on the inside of the original square outside of the rotated square are also congruent 30-60-90 triangles. Noting this, we can do some labelling: | ||
<asy> | <asy> | ||
| Line 9: | Line 171: | ||
path p = box((0,0), (1,1)); | path p = box((0,0), (1,1)); | ||
draw(p, black + linewidth(2.0pt)); | draw(p, black + linewidth(2.0pt)); | ||
| − | draw(rotate(30,(1/2,1/2))*p,black + linewidth(2.0pt)); | + | draw(rotate(30,(1/2,1/2))*p,black + linewidth(2.0pt)); /*Rotate 60 |
| − | + | degrees*/ | |
| − | + | label("$y$",(0.1,-0.05)); | |
| − | + | label("$x$",(0.4,0.05)); | |
| − | + | label("$y\sqrt{3}$",(0.8,-0.05)); | |
| − | + | label("$\frac{x}{2}$",(0.22,-0.12)); | |
| − | + | label("$\frac{x\sqrt{3}}{2}$",(0.5,-0.15)); | |
| − | + | label("$2y$",(0.8,0.15)); | |
| + | label("$y$",(1.05,0.1)); | ||
| + | label("$\frac{x}{2}$",(1.12,0.22)); | ||
| + | |||
| + | </asy> | ||
| + | |||
| + | Since the side lengths of the squares must be the same, and they are both 6, we have a system of equations; | ||
| + | <cmath>y+x+y\sqrt{3} = 6</cmath> | ||
| + | <cmath>\frac{x\sqrt{3}}{2} + 2y + \frac{x}{2} = 6</cmath> | ||
| + | |||
| + | We solve this to get <math>x = 6-2\sqrt{3}</math> and <math>y = 3-\sqrt{3}</math>. | ||
| + | |||
| + | The area of each triangle is <math>\frac{x}{2} \cdot \frac{x\sqrt{3}}{2} \cdot \frac{1}{2} = 6\sqrt{3} - 9</math> by plugging in <math>x</math>. | ||
| + | The rotated 60 degree square is the same thing as rotating it 30 degrees counterclockwise, so it's triangles that jut out of the square will be congruent to the triangles we have found, and therefore they will have the same area. | ||
| + | |||
| + | Unfortunately, when drawing all three squares, we see the two triangles overlap; take the very top for example. | ||
| + | |||
| + | <asy> | ||
| + | import olympiad; | ||
| + | size(10cm); | ||
| + | pair A,B,C,D,E,F,G; | ||
| + | A = (0.211,0); B=(0.3657,0); C = (0.63397,0); D = (0.789,0); E = (0.31666,0.1823); F=(0.5,0.077); G=(0.68334,0.1823); | ||
| + | draw((0,0)--(1,0),black+linewidth(2pt)); | ||
| + | draw(A--E--C--cycle); | ||
| + | draw(B--D--G--cycle); | ||
| + | label("$A$",A,S); | ||
| + | label("$B$",B,S); | ||
| + | label("$C$",C,S); | ||
| + | label("$D$",D,S); | ||
| + | label("$E$",E,N); | ||
| + | label("$F$",F,N); | ||
| + | label("$G$",G,N); | ||
</asy> | </asy> | ||
| − | + | The area of this shape is twice the area of each of the triangles that we have already found minus the area of the small triangle that is overlapped by the two by PIE. Now we only need to find the area of <math>\bigtriangleup BCF</math>. | |
| − | + | <math>\angle GBD \cong \angle ECA \cong 30^{\circ}</math> and by symmetry <math>\bigtriangleup BCF</math> is isosceles, so it is a 30-30-120 triangle. If we draw a perpendicular, we split it into two 30-60-90 triangles; | |
| − | + | ||
| + | <asy> | ||
| + | import olympiad; | ||
| + | size(10cm); | ||
| + | pair A,B,C,D,E,F,G; | ||
| + | A = (0.211,0); B=(0.3657,0); C = (0.63397,0); D = (0.789,0); E = (0.31666,0.1823); F=(0.5,0.077); G=(0.68334,0.1823); | ||
| + | draw((0,0)--(1,0),black+linewidth(2pt)); | ||
| + | draw(A--E--C--cycle); | ||
| + | draw(B--D--G--cycle); | ||
| + | draw(F--(0.5,0)); | ||
| + | label("$A$",A,S); | ||
| + | label("$B$",B,S); | ||
| + | label("$C$",C,S); | ||
| + | label("$D$",D,S); | ||
| + | label("$E$",E,N); | ||
| + | label("$F$",F,N); | ||
| + | label("$G$",G,N); | ||
| + | label("$H$",(0.5,0),S); | ||
| + | </asy> | ||
| + | |||
| + | By symmetry, the distance from A to the edge of the square is equal to the distance from D to the edge of the square is equal to <math>y</math>. AC = BD = <math>x</math>, and the side length of the square is 6, so we use PIE to obtain <cmath>x+x-BC = 6-y-y \implies BC = 12 - 6\sqrt{3}</cmath> | ||
| + | To find the height of <math>\bigtriangleup BFC</math>, we see that <math>HC = \frac{BC}{2} = 6-3\sqrt{3}</math>. Then by 30-60-90 triangles, <math>HF = \frac{HC}{\sqrt{3}} = 2\sqrt{3} - 3</math>. Finally, the area of <math>\bigtriangleup BFC = \frac{BC \cdot HF}{2} = 21\sqrt{3}-36</math>. | ||
| + | |||
| + | Putting it all together, the area of the entire diagram is the area of the square plus four of these triangle-triangle intersections. The area of these intersections by PIE is <math>2 \cdot [ACE] - [BFC] = 12\sqrt{3}-18-(21\sqrt{3}-36) = 18-9\sqrt{3}</math>. | ||
| + | Therefore the total area is <math>36 + 4 \cdot(18-9\sqrt{3}) = 36 + 72 - 36 \sqrt{3} = 108 - 36\sqrt{3}</math>. | ||
| + | |||
| + | Thus <math>a + b + c = 108+36+3 = 147 = \boxed{\textbf{(E) }147}</math>. | ||
| − | ~ | + | ~KingRavi |
| − | == Solution | + | == Solution 5 == |
As shown in [[:Image:2021_AMC_12B_(Nov)_Problem_15,_sol.png]], all 12 vertices of three squares form a regular dodecagon (12-gon). | As shown in [[:Image:2021_AMC_12B_(Nov)_Problem_15,_sol.png]], all 12 vertices of three squares form a regular dodecagon (12-gon). | ||
Denote by <math>O</math> the center of this dodecagon. | Denote by <math>O</math> the center of this dodecagon. | ||
| Line 43: | Line 262: | ||
<cmath> | <cmath> | ||
\begin{align*} | \begin{align*} | ||
| − | & | + | & \ [ABCDEFGHIJKL] - 12[MAB] \\ |
| − | & = 12 | + | & = 12 [OAB] - 12 [MAB] \\ |
& = 12 \cdot \frac{1}{2} OA \cdot OB \sin \angle AOB | & = 12 \cdot \frac{1}{2} OA \cdot OB \sin \angle AOB | ||
- 12 \cdot \frac{1}{2} MA \cdot MB \sin \angle AMB \\ | - 12 \cdot \frac{1}{2} MA \cdot MB \sin \angle AMB \\ | ||
& = 6 OA^2 \sin \angle AOB - 6 MA^2 \sin \angle AMB \\ | & = 6 OA^2 \sin \angle AOB - 6 MA^2 \sin \angle AMB \\ | ||
| − | & = 108 - 36 \sqrt{3} | + | & = 108 - 36\sqrt{3} |
\end{align*} | \end{align*} | ||
</cmath> | </cmath> | ||
| Line 56: | Line 275: | ||
~Steven Chen (www.professorchenedu.com) | ~Steven Chen (www.professorchenedu.com) | ||
| − | ==Solution 3 (30-60-90 | + | ~stjwyl (adjusted for readability aka minor edits) |
| + | |||
| + | Note: If you have square brakets around a specified polygon (i.e. [ABCD]), it means the writer is referring to the area of that polygon. | ||
| + | |||
| + | == Solution 6 == | ||
| + | [[Image:Drawing_Split_into_12_pieces.png|thumb|center|4000|]] | ||
| + | |||
| + | First, we can separate the shape into 12 congruent kites. The area of the figure can be determined by finding the area of one kite and multiplying it by 12. In order to to get the area of one kite, we need to find its diagonals, shown in blue. | ||
| + | [[Image:Shorter Diagonal.png|thumb|center|2000|]] | ||
| + | |||
| + | We notice that angle FCE is <math>\frac{360^\circ}{12} = 30^\circ</math>. Also, we know that CD is half of AB, so it has a length of 3. Now, we can find the lengths of FC and FD using the 30-60-90 triangle. We find that FC is <math>2\sqrt{3}</math> and FD is <math>\sqrt{3}</math>. Since FC is congruent to CE, CE is also <math>2\sqrt{3}</math>. Using this information, we can conclude that ED is <math>2\sqrt{3}-3</math>. | ||
| + | [[Image:Copy of Shorter Diagonal.png|thumb|center|2000|]] | ||
| + | |||
| + | Now, we can find the shorter diagonal by using the Pythagorean theorem: | ||
| + | <cmath> | ||
| + | \begin{align*} | ||
| + | & {\rm FC}^2 = \sqrt{3}^2 + (2\sqrt{3}-3)^2 \\ | ||
| + | & {\rm FC} = \sqrt{24- 12\sqrt{3}} | ||
| + | \end{align*} | ||
| + | </cmath> | ||
| + | [[Image:Longer Diagonal.png|thumb|center|2000|]] | ||
| + | |||
| + | We can find the longer diagonal of the kite by looking at one of the square sheets of paper. We know that the side of the square has a length of 6, so the diagonal of the square must be <math>6\sqrt{2}</math>. The longer diagonal of the kite is half of this length, so it has a length of <math>3\sqrt{2}</math>. | ||
| + | |||
| + | The area of the entire figure is | ||
| + | <cmath> | ||
| + | \begin{align*} | ||
| + | & = 12 \cdot\frac{{\rm d_1*d_2}}{2} \\ | ||
| + | & = 12 \cdot\frac{3\sqrt{2}\cdot\sqrt{24- 12\sqrt{3}}}{2} \\ | ||
| + | & = 12 \cdot\frac{6\sqrt{12- 6\sqrt{3}}}{2} \\ | ||
| + | & = 36 \sqrt{12- 6\sqrt{3}} | ||
| + | \end{align*} | ||
| + | </cmath> | ||
| + | |||
| + | Now we can use algebra to make our answer look a little nicer. | ||
| + | <cmath> | ||
| + | \begin{align*} | ||
| + | & a-\sqrt{b} = \sqrt{12- 6\sqrt{3}} \\ | ||
| + | & (a-\sqrt{b})^2 = (\sqrt{12- 6\sqrt{3}})^2 \\ | ||
| + | & a^2-2a\sqrt{b}+b = 12 - 6\sqrt{3}\\ | ||
| + | &\\ | ||
| + | &a^2+b = 12 \\ | ||
| + | &2a\sqrt{b} = 6\sqrt{3} \\ | ||
| + | & a = 3, b = 3 \\ | ||
| + | &\\ | ||
| + | & a-\sqrt{b} = \sqrt{12- 6\sqrt{3}} = 3 - \sqrt{3} | ||
| + | \end{align*} | ||
| + | </cmath> | ||
| + | |||
| + | The area of the entire region is <math>36(3 - \sqrt{3})</math>, or <math>108 - 36\sqrt{3}</math>. | ||
| + | |||
| + | Therefore, <math>a + b + c = 108 + 36+ 3 = 147 = \boxed{E}</math>. | ||
| + | |||
| + | ~JavaWhiz12 | ||
| + | |||
| + | == Solution 7 == | ||
| + | Let <math>O</math> be the center of the polygon, <math>A</math> be the bottom right corner of the first square, <math>C</math> be the next vertex to the left of <math>A</math>, and <math>M</math> be the midpoint between <math>A</math> and <math>B</math>, where <math>B</math> is the bottom left corner of the first square. Note that because there are three <math>90^{\circ}</math> squares separated by <math>\frac{90^{\circ}}{3} = 30^{\circ}</math>, each side of the 24-sided polygon is equal in length, meaning to calculate the area of the whole polygon, we find the area of <math>\bigtriangleup OAC</math> and multiply by 24. | ||
| + | |||
| + | |||
| + | To find <math>[\bigtriangleup OAC]</math>, we already know the height <math>\overline{OM}</math> is the sidelength of the square over <math>2</math>, or <math>\frac{6}{2}=3</math>, so we just need the length of the base <math>\overline{AC}</math>. Notice that <math>\bigtriangleup OCM</math> is a <math>30-60-90</math> triangle since <math>\angle COM = \frac{360^{\circ}}{12} = 30^{\circ}</math>, so <math>\overline{CM} = \frac{\overline{OM}}{\sqrt{3}} = \frac{3}{\sqrt{3}} = \sqrt{3}</math>. Then <math>\overline{AC} = \overline{AM} - \overline{CM} = \frac{6}{2} - \sqrt{3} = 3 - \sqrt{3}</math>, so | ||
| + | <cmath> | ||
| + | \begin{align*} | ||
| + | & [\bigtriangleup AOC] = \frac{1}{2} \cdot \overline{OM} \cdot \overline{AC} \\ | ||
| + | & = \frac{1}{2} (3)(3 - \sqrt{3}) \\ | ||
| + | & = \frac{9 - 3\sqrt{3}}{2} | ||
| + | \end{align*} | ||
| + | </cmath> | ||
| + | |||
| + | Then the whole area of the polygon is <math>\frac{9 - 3\sqrt{3}}{2} \cdot 24 = 108 - 36\sqrt{3}</math>. The desired solution is then <math>108 + 36 + 3 = 147</math>, so the answer is <math>\boxed{\textbf{(E) 147}}</math>. | ||
| − | + | ~Tacozxyt | |
| − | + | ==Video Solution 1 by Power of Logic (math2718281828459)== | |
| − | + | https://youtu.be/i8h8cq_WBjA | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ~math2718281828459 | |
| − | + | ==Video Solution 2 by Interstigation (with some trigonometry)== | |
| + | https://www.youtube.com/watch?v=8GgGXsB3yjU | ||
| − | + | ~Interstigation | |
| − | + | ==Video Solution 3 by WhyMath== | |
| − | + | https://youtu.be/kP3jD1-aVzY | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | ~savannahsolver | ||
| − | + | ==Video Solution 4 (1 min)== | |
| + | https://youtu.be/oKPQh9lU0X4 | ||
| − | Solution | + | ==Video Solution by TheBeautyofMath== |
| + | https://youtu.be/YD9J394zeig | ||
| − | ~ | + | ~IceMatrix |
==See Also== | ==See Also== | ||
{{AMC10 box|year=2021 Fall|ab=B|num-a=19|num-b=17}} | {{AMC10 box|year=2021 Fall|ab=B|num-a=19|num-b=17}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Latest revision as of 21:23, 23 July 2024
Contents
- 1 Problem
- 2 Solution 1
- 3 Solution 2 (15-75-90 triangles)
- 4 Solution 3
- 5 Solution 4 (30-60-90 Triangles)
- 6 Solution 5
- 7 Solution 6
- 8 Solution 7
- 9 Video Solution 1 by Power of Logic (math2718281828459)
- 10 Video Solution 2 by Interstigation (with some trigonometry)
- 11 Video Solution 3 by WhyMath
- 12 Video Solution 4 (1 min)
- 13 Video Solution by TheBeautyofMath
- 14 See Also
Problem
Three identical square sheets of paper each with side length ![]() are stacked on top of each other. The middle sheet is rotated clockwise
are stacked on top of each other. The middle sheet is rotated clockwise ![]() about its center and the top sheet is rotated clockwise
about its center and the top sheet is rotated clockwise ![]() about its center, resulting in the
about its center, resulting in the ![]() -sided polygon shown in the figure below. The area of this polygon can be expressed in the form
-sided polygon shown in the figure below. The area of this polygon can be expressed in the form ![]() , where
, where ![]() ,
, ![]() , and
, and ![]() are positive integers, and
are positive integers, and ![]() is not divisible by the square of any prime. What is
is not divisible by the square of any prime. What is ![]()
![[asy] defaultpen(fontsize(8)+0.8); size(150); pair O,A1,B1,C1,A2,B2,C2,A3,B3,C3,A4,B4,C4; real x=45, y=90, z=60; O=origin; A1=dir(x); A2=dir(x+y); A3=dir(x+2y); A4=dir(x+3y); B1=dir(x-z); B2=dir(x+y-z); B3=dir(x+2y-z); B4=dir(x+3y-z); C1=dir(x-2z); C2=dir(x+y-2z); C3=dir(x+2y-2z); C4=dir(x+3y-2z); draw(A1--A2--A3--A4--A1, gray+0.25+dashed); filldraw(B1--B2--B3--B4--cycle, white, gray+dashed+linewidth(0.25)); filldraw(C1--C2--C3--C4--cycle, white, gray+dashed+linewidth(0.25)); dot(O); pair P1,P2,P3,P4,Q1,Q2,Q3,Q4,R1,R2,R3,R4; P1=extension(A1,A2,B1,B2); Q1=extension(A1,A2,C3,C4); P2=extension(A2,A3,B2,B3); Q2=extension(A2,A3,C4,C1); P3=extension(A3,A4,B3,B4); Q3=extension(A3,A4,C1,C2); P4=extension(A4,A1,B4,B1); Q4=extension(A4,A1,C2,C3); R1=extension(C2,C3,B2,B3); R2=extension(C3,C4,B3,B4); R3=extension(C4,C1,B4,B1); R4=extension(C1,C2,B1,B2); draw(A1--P1--B2--R1--C3--Q1--A2); draw(A2--P2--B3--R2--C4--Q2--A3); draw(A3--P3--B4--R3--C1--Q3--A4); draw(A4--P4--B1--R4--C2--Q4--A1); [/asy]](http://latex.artofproblemsolving.com/7/e/b/7eb8841b95d6e1c451addf20403c4e540f176116.png)
![]()
Solution 1
![[asy] defaultpen(fontsize(8)+0.8); size(100); pair A=(0,0); pair B=(1.732,3); pair C=(3,3); pair D=(3,1.732); draw(A--(0,3)--C--(3,0)--A, lightgray+dashed); draw(A--B--C--A); draw(A--D--C, gray); label("$A$",A,W); label("$B$",B,N); label("$C$",C,NE); label("$D$",D,E); label("$E$",(0,3),NW); label("$F$",(3,0),E); [/asy]](http://latex.artofproblemsolving.com/6/4/f/64f3c31b5b88bfd1d71ed15cecc5de817a573f8e.png) The
The ![]() -sided polygon is made out of
-sided polygon is made out of ![]() shapes like
shapes like ![]() . Then
. Then ![]() , and
, and ![]() , so
, so ![]() . Then
. Then ![]() ; therefore
; therefore ![]() . Thus
. Thus
![]() and the required area is
and the required area is ![]() . Finally
. Finally ![]() .
~lopkiloinm
.
~lopkiloinm
Solution 2 (15-75-90 triangles)
![[asy] defaultpen(fontsize(8)+0.8); size(150); pair O,A1,B1,C1,A2,B2,C2,A3,B3,C3,A4,B4,C4; real x=45, y=90, z=60; O=origin; A1=dir(x); A2=dir(x+y); A3=dir(x+2y); A4=dir(x+3y); B1=dir(x-z); B2=dir(x+y-z); B3=dir(x+2y-z); B4=dir(x+3y-z); C1=dir(x-2z); C2=dir(x+y-2z); C3=dir(x+2y-2z); C4=dir(x+3y-2z); draw(A1--A2--A3--A4--A1, gray+0.25+dashed); filldraw(B1--B2--B3--B4--cycle, white, gray+dashed+linewidth(0.25)); filldraw(C1--C2--C3--C4--cycle, white, gray+dashed+linewidth(0.25)); filldraw(O--C3--B2--cycle, white, black+linewidth(0.5)); dot(O); label("$O$",O,W); label("$B$",C3,N); label("$C$",B2,N); label("$A$",(0,0.8),S); pair P1,P2,P3,P4,Q1,Q2,Q3,Q4,R1,R2,R3,R4; P1=extension(A1,A2,B1,B2); Q1=extension(A1,A2,C3,C4); P2=extension(A2,A3,B2,B3); Q2=extension(A2,A3,C4,C1); P3=extension(A3,A4,B3,B4); Q3=extension(A3,A4,C1,C2); P4=extension(A4,A1,B4,B1); Q4=extension(A4,A1,C2,C3); R1=extension(C2,C3,B2,B3); R2=extension(C3,C4,B3,B4); R3=extension(C4,C1,B4,B1); R4=extension(C1,C2,B1,B2); draw(A1--P1--B2--R1--C3--Q1--A2); draw(A2--P2--B3--R2--C4--Q2--A3); draw(A3--P3--B4--R3--C1--Q3--A4); draw(A4--P4--B1--R4--C2--Q4--A1); [/asy]](http://latex.artofproblemsolving.com/1/e/2/1e28d3773e9fcc7541cb5c53586dfb20929c076d.png)
Break the ![]() -gon as shown so that there are
-gon as shown so that there are ![]() copies of quadrilateral
copies of quadrilateral ![]() . We can find the area of this quadrilateral by finding the area of triangle
. We can find the area of this quadrilateral by finding the area of triangle ![]() and subtracting the area of triangle
and subtracting the area of triangle ![]() .
.
The angle from ![]() to one of the vertices of the original square is
to one of the vertices of the original square is ![]() , and this point rotates
, and this point rotates ![]() , so the angle that
, so the angle that ![]() makes with the horizontal is
makes with the horizontal is ![]() .
.
Let ![]() be the intersection of
be the intersection of ![]() with
with ![]() . Since
. Since ![]() and
and ![]() are both isosceles,
are both isosceles, ![]() forms a right angle with
forms a right angle with ![]() . Furthermore,
. Furthermore, ![]() .
.
![[asy] import olympiad; pair O,C,D; D=(0,4); O=(0,0); C=(1.1,4); draw(O--C--D--cycle); label("$D$",D,N); label("$C$",C,N); label("$O$",O,S); path angle = anglemark(C, O, D); draw(rightanglemark(O, D, C)); [/asy]](http://latex.artofproblemsolving.com/0/8/0/080091f59b2fe1e330417ffefde33d3af9bc542e.png)
Note that ![]() is equal to
is equal to ![]() because it is half the diagonal of the square with side length
because it is half the diagonal of the square with side length ![]() . We can now split up the
. We can now split up the ![]() into
into ![]() and
and ![]() triangles to find the height and length of the triangle:
triangles to find the height and length of the triangle:
![[asy] import olympiad; pair O,C,D,E; D=(0,4); O=(0,0); C=(1.1,4); E=(0,2.1); draw(O--C--D--cycle); label("$D$",D,N); label("$C$",C,N); label("$O$",O,S); label("$3\sqrt{2}$",(1.3,2),E); path angle = anglemark(C, O, D); draw(rightanglemark(O, D, C)); draw(C--E); label("$E$",E,W); label("$x$",(0.5,4),N); label("$x\sqrt{3}$",(-0.1,3.2),W); label("$2x$",(-0.1,1),W); [/asy]](http://latex.artofproblemsolving.com/1/3/9/13966fe2b77cb29b8c1696c395efd6f28df9d52e.png)
Now we have use Pythagorean: ![]()
![]()
Now note that ![]() must be in the form of
must be in the form of ![]() . Therefore,
. Therefore, ![]() . We can guess that
. We can guess that ![]() . Sure enough,
. Sure enough, ![]() , so
, so ![]() . Then the height of the triangle is
. Then the height of the triangle is ![]() .
.
The area of triangle ![]() is equal to the length times the height of triangle
is equal to the length times the height of triangle ![]() since this triangle has half the area of the full triangle. Therefore the area of triangle
since this triangle has half the area of the full triangle. Therefore the area of triangle ![]() .
.
Now we look at triangle ![]() .
. ![]() because
because ![]() is the diagonal of a square, and
is the diagonal of a square, and ![]() is
is ![]() as we saw earlier. Therefore,
as we saw earlier. Therefore, ![]() . Because both these angles are
. Because both these angles are ![]() ,
, ![]() .
.
We can now split triangle ![]() into two congruent
into two congruent ![]() triangles, and we know the base of each since
triangles, and we know the base of each since ![]() .
.
The height of these triangles is  . Therefore the area of this triangle is
. Therefore the area of this triangle is ![]()
Therefore the total area of this segment is ![]() . Multiplying by
. Multiplying by ![]() to find the entire area, the area of the figure is
to find the entire area, the area of the figure is ![]() and the answer is
and the answer is ![]()
~KingRavi
Solution 3
First note the useful fact that if ![]() is the circumradius of a dodecagon (
is the circumradius of a dodecagon (![]() -gon) the area of the figure is
-gon) the area of the figure is ![]() If we connect the vertices of the
If we connect the vertices of the ![]() squares we get a dodecagon. The radius of circumcircle of the dodecagon is simply half the diagonal of the square, which is
squares we get a dodecagon. The radius of circumcircle of the dodecagon is simply half the diagonal of the square, which is ![]() Thus the area of the dodecagon is
Thus the area of the dodecagon is ![]() But, the problem asked for the area of the combined figure which was made from the rotated squares. This area is the area of the dodecagon, which was found, subtracting the
But, the problem asked for the area of the combined figure which was made from the rotated squares. This area is the area of the dodecagon, which was found, subtracting the ![]() isosceles triangles, which are formed when connecting the vertices of the squares to created the dodecagon. To find this area, we need to know the base of the isosceles triangle, call this
isosceles triangles, which are formed when connecting the vertices of the squares to created the dodecagon. To find this area, we need to know the base of the isosceles triangle, call this ![]() Then, we can use the Law of Cosines on the triangle that is formed from the two vertices of the square and the center of the square. After computing, we get that
Then, we can use the Law of Cosines on the triangle that is formed from the two vertices of the square and the center of the square. After computing, we get that ![]() Realize that the
Realize that the ![]() isosceles are congruent with an angle measure of
isosceles are congruent with an angle measure of ![]() this means that we can create
this means that we can create ![]() congruent equilateral triangles with side length of
congruent equilateral triangles with side length of ![]() The area of the equilateral triangle is
The area of the equilateral triangle is ![]() Thus, the area of all the twelve small equilateral traingles are
Thus, the area of all the twelve small equilateral traingles are ![]() . Thus, the requested area is
. Thus, the requested area is ![]() Thus,
Thus, ![]() so the answer is
so the answer is ![]()
~NH14
Solution 4 (30-60-90 Triangles)
To make things simpler, let's take only the original sheet and the 30 degree rotated sheet. Then the diagram is this;
![[asy] size(10cm,0); path p = box((0,0), (1,1)); draw(p, black + linewidth(2.0pt)); draw(rotate(30,(1/2,1/2))*p,black + linewidth(2.0pt)); /*Rotate 60 degrees*/ [/asy]](http://latex.artofproblemsolving.com/1/d/1/1d18fa448a9d67e0133a366e5ace7d169451f836.png)
The area of this diagram is the original square plus the area of the four triangles that 'jut' out of the square. Because the square is rotated ![]() , each triangle is a 30-60-90 triangle. Similarly, the triangles that are bounded on the inside of the original square outside of the rotated square are also congruent 30-60-90 triangles. Noting this, we can do some labelling:
, each triangle is a 30-60-90 triangle. Similarly, the triangles that are bounded on the inside of the original square outside of the rotated square are also congruent 30-60-90 triangles. Noting this, we can do some labelling:
![[asy] size(10cm,0); path p = box((0,0), (1,1)); draw(p, black + linewidth(2.0pt)); draw(rotate(30,(1/2,1/2))*p,black + linewidth(2.0pt)); /*Rotate 60 degrees*/ label("$y$",(0.1,-0.05)); label("$x$",(0.4,0.05)); label("$y\sqrt{3}$",(0.8,-0.05)); label("$\frac{x}{2}$",(0.22,-0.12)); label("$\frac{x\sqrt{3}}{2}$",(0.5,-0.15)); label("$2y$",(0.8,0.15)); label("$y$",(1.05,0.1)); label("$\frac{x}{2}$",(1.12,0.22)); [/asy]](http://latex.artofproblemsolving.com/9/c/d/9cd2cf7a32b282cd81ea1059fb9218a0b425d1df.png)
Since the side lengths of the squares must be the same, and they are both 6, we have a system of equations;
![]()
![]()
We solve this to get ![]() and
and ![]() .
.
The area of each triangle is ![]() by plugging in
by plugging in ![]() .
.
The rotated 60 degree square is the same thing as rotating it 30 degrees counterclockwise, so it's triangles that jut out of the square will be congruent to the triangles we have found, and therefore they will have the same area.
Unfortunately, when drawing all three squares, we see the two triangles overlap; take the very top for example.
![[asy] import olympiad; size(10cm); pair A,B,C,D,E,F,G; A = (0.211,0); B=(0.3657,0); C = (0.63397,0); D = (0.789,0); E = (0.31666,0.1823); F=(0.5,0.077); G=(0.68334,0.1823); draw((0,0)--(1,0),black+linewidth(2pt)); draw(A--E--C--cycle); draw(B--D--G--cycle); label("$A$",A,S); label("$B$",B,S); label("$C$",C,S); label("$D$",D,S); label("$E$",E,N); label("$F$",F,N); label("$G$",G,N); [/asy]](http://latex.artofproblemsolving.com/f/1/6/f16ee002ef8b937fe059cd2d08ae91a2002615af.png)
The area of this shape is twice the area of each of the triangles that we have already found minus the area of the small triangle that is overlapped by the two by PIE. Now we only need to find the area of ![]() .
.
![]() and by symmetry
and by symmetry ![]() is isosceles, so it is a 30-30-120 triangle. If we draw a perpendicular, we split it into two 30-60-90 triangles;
is isosceles, so it is a 30-30-120 triangle. If we draw a perpendicular, we split it into two 30-60-90 triangles;
![[asy] import olympiad; size(10cm); pair A,B,C,D,E,F,G; A = (0.211,0); B=(0.3657,0); C = (0.63397,0); D = (0.789,0); E = (0.31666,0.1823); F=(0.5,0.077); G=(0.68334,0.1823); draw((0,0)--(1,0),black+linewidth(2pt)); draw(A--E--C--cycle); draw(B--D--G--cycle); draw(F--(0.5,0)); label("$A$",A,S); label("$B$",B,S); label("$C$",C,S); label("$D$",D,S); label("$E$",E,N); label("$F$",F,N); label("$G$",G,N); label("$H$",(0.5,0),S); [/asy]](http://latex.artofproblemsolving.com/0/c/2/0c25434b9a0f4f8f006dc23cc1f6dd3c27858cbf.png)
By symmetry, the distance from A to the edge of the square is equal to the distance from D to the edge of the square is equal to ![]() . AC = BD =
. AC = BD = ![]() , and the side length of the square is 6, so we use PIE to obtain
, and the side length of the square is 6, so we use PIE to obtain ![]() To find the height of
To find the height of ![]() , we see that
, we see that ![]() . Then by 30-60-90 triangles,
. Then by 30-60-90 triangles, ![]() . Finally, the area of
. Finally, the area of ![]() .
.
Putting it all together, the area of the entire diagram is the area of the square plus four of these triangle-triangle intersections. The area of these intersections by PIE is ![]() .
Therefore the total area is
.
Therefore the total area is ![]() .
.
Thus ![]() .
.
~KingRavi
Solution 5
As shown in Image:2021_AMC_12B_(Nov)_Problem_15,_sol.png, all 12 vertices of three squares form a regular dodecagon (12-gon).
Denote by ![]() the center of this dodecagon.
the center of this dodecagon.
Hence, ![]() .
.
Because the length of a side of a square is 6, ![]() .
.
Hence, ![]() .
.
We notice that ![]() .
Hence,
.
Hence, ![]() .
.
Therefore, the area of the region that three squares cover is
![\begin{align*} & \ [ABCDEFGHIJKL] - 12[MAB] \\ & = 12 [OAB] - 12 [MAB] \\ & = 12 \cdot \frac{1}{2} OA \cdot OB \sin \angle AOB - 12 \cdot \frac{1}{2} MA \cdot MB \sin \angle AMB \\ & = 6 OA^2 \sin \angle AOB - 6 MA^2 \sin \angle AMB \\ & = 108 - 36\sqrt{3} \end{align*}](http://latex.artofproblemsolving.com/a/0/6/a068e1fdf82040116a0fc68f38a988271000e12b.png)
Therefore, the answer is ![]() .
.
~Steven Chen (www.professorchenedu.com)
~stjwyl (adjusted for readability aka minor edits)
Note: If you have square brakets around a specified polygon (i.e. [ABCD]), it means the writer is referring to the area of that polygon.
Solution 6
First, we can separate the shape into 12 congruent kites. The area of the figure can be determined by finding the area of one kite and multiplying it by 12. In order to to get the area of one kite, we need to find its diagonals, shown in blue.
We notice that angle FCE is ![]() . Also, we know that CD is half of AB, so it has a length of 3. Now, we can find the lengths of FC and FD using the 30-60-90 triangle. We find that FC is
. Also, we know that CD is half of AB, so it has a length of 3. Now, we can find the lengths of FC and FD using the 30-60-90 triangle. We find that FC is ![]() and FD is
and FD is ![]() . Since FC is congruent to CE, CE is also
. Since FC is congruent to CE, CE is also ![]() . Using this information, we can conclude that ED is
. Using this information, we can conclude that ED is ![]() .
.
Now, we can find the shorter diagonal by using the Pythagorean theorem:

We can find the longer diagonal of the kite by looking at one of the square sheets of paper. We know that the side of the square has a length of 6, so the diagonal of the square must be ![]() . The longer diagonal of the kite is half of this length, so it has a length of
. The longer diagonal of the kite is half of this length, so it has a length of ![]() .
.
The area of the entire figure is

Now we can use algebra to make our answer look a little nicer.

The area of the entire region is ![]() , or
, or ![]() .
.
Therefore, ![]() .
.
~JavaWhiz12
Solution 7
Let ![]() be the center of the polygon,
be the center of the polygon, ![]() be the bottom right corner of the first square,
be the bottom right corner of the first square, ![]() be the next vertex to the left of
be the next vertex to the left of ![]() , and
, and ![]() be the midpoint between
be the midpoint between ![]() and
and ![]() , where
, where ![]() is the bottom left corner of the first square. Note that because there are three
is the bottom left corner of the first square. Note that because there are three ![]() squares separated by
squares separated by ![]() , each side of the 24-sided polygon is equal in length, meaning to calculate the area of the whole polygon, we find the area of
, each side of the 24-sided polygon is equal in length, meaning to calculate the area of the whole polygon, we find the area of ![]() and multiply by 24.
and multiply by 24.
To find ![]() , we already know the height
, we already know the height ![]() is the sidelength of the square over
is the sidelength of the square over ![]() , or
, or ![]() , so we just need the length of the base
, so we just need the length of the base ![]() . Notice that
. Notice that ![]() is a
is a ![]() triangle since
triangle since ![]() , so
, so ![]() . Then
. Then ![]() , so
, so
![\begin{align*} & [\bigtriangleup AOC] = \frac{1}{2} \cdot \overline{OM} \cdot \overline{AC} \\ & = \frac{1}{2} (3)(3 - \sqrt{3}) \\ & = \frac{9 - 3\sqrt{3}}{2} \end{align*}](http://latex.artofproblemsolving.com/9/b/0/9b089749dff4dbbe7b26e0eb35fb5dc43f003781.png)
Then the whole area of the polygon is ![]() . The desired solution is then
. The desired solution is then ![]() , so the answer is
, so the answer is ![]() .
.
~Tacozxyt
Video Solution 1 by Power of Logic (math2718281828459)
~math2718281828459
Video Solution 2 by Interstigation (with some trigonometry)
https://www.youtube.com/watch?v=8GgGXsB3yjU
~Interstigation
Video Solution 3 by WhyMath
~savannahsolver
Video Solution 4 (1 min)
Video Solution by TheBeautyofMath
~IceMatrix
See Also
| 2021 Fall AMC 10B (Problems • Answer Key • Resources) | ||
| Preceded by Problem 17 |
Followed by Problem 19 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.