Difference between revisions of "Gossard perspector"
(→Gossard perspector and Gossard triangle for equilateral triangle) |
(→Dao Thanh Oai Generalization) |
||
| (26 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
==Gossard perspector X(402) and Gossard triangle== | ==Gossard perspector X(402) and Gossard triangle== | ||
| − | Euler proved that the Euler line of a given triangle together with two of its sides forms a triangle whose Euler line is parallel with the third side of the given triangle. | + | In <math>1765</math> Leonhard Euler proved that in any triangle, the orthocenter, circumcenter and centroid are collinear. We name this line the Euler line. Soon he proved that the Euler line of a given triangle together with two of its sides forms a triangle whose Euler line is in parallel with the third side of the given triangle. |
| − | Gossard proved that | + | Professor Harry Clinton Gossard in <math>1916</math> proved that three Euler lines of the triangles formed by the Euler line and the sides, taken by two, of a given triangle, form a triangle which is perspective with the given triangle and has the same Euler line. The center of the perspective now is known as the Gossard perspector or the Kimberling point <math>X(402).</math> It is the crosspoint of Gauss line and Euler line. |
| + | |||
| + | Let triangle <math>\triangle ABC</math> be given. The Euler line crosses lines <math>AB, BC,</math> and <math>AC</math> at points <math>D, E,</math> and <math>F.</math> | ||
| + | |||
| + | On <math>13/01/2023</math> it was found that the Gossard perspector is the centroid of the points <math>A, B, C, D, E, F.</math> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
==Gossard perspector of right triangle== | ==Gossard perspector of right triangle== | ||
| Line 26: | Line 32: | ||
'''vladimir.shelomovskii@gmail.com, vvsss''' | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
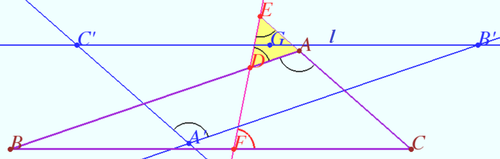
| − | ==Gossard perspector and Gossard triangle for | + | ==Gossard perspector and Gossard triangle for isosceles triangle== |
[[File:Gossard equilateral.png|500px|right]] | [[File:Gossard equilateral.png|500px|right]] | ||
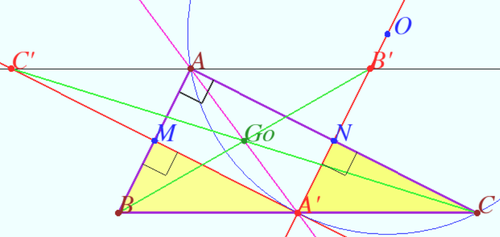
| − | It is clear that the Euler line of | + | It is clear that the Euler line of isosceles <math>\triangle ABC (AB = AC)</math> meet the sidelines <math>BC, CA</math> and <math>AB</math> of <math>\triangle ABC</math> at <math>A'</math> and <math>A,</math> where <math>A'</math> is the midpoint of <math>BC.</math> |
Let <math>\triangle A'B'C'</math> be the triangle formed by the Euler lines of the <math>\triangle AA'B, \triangle AA'C,</math> and the line <math>l</math> contains <math>A</math> and parallel to <math>BC,</math> the vertex <math>B'</math> being the intersection of the Euler line of the <math>\triangle AA'C</math> and <math>l,</math> the vertex <math>C'</math> being the intersection of the Euler line of the <math>\triangle AA'B</math> and <math>l.</math> | Let <math>\triangle A'B'C'</math> be the triangle formed by the Euler lines of the <math>\triangle AA'B, \triangle AA'C,</math> and the line <math>l</math> contains <math>A</math> and parallel to <math>BC,</math> the vertex <math>B'</math> being the intersection of the Euler line of the <math>\triangle AA'C</math> and <math>l,</math> the vertex <math>C'</math> being the intersection of the Euler line of the <math>\triangle AA'B</math> and <math>l.</math> | ||
| Line 34: | Line 40: | ||
We call the triangle <math>\triangle A'B'C'</math> as the Gossard triangle of <math>\triangle ABC.</math> | We call the triangle <math>\triangle A'B'C'</math> as the Gossard triangle of <math>\triangle ABC.</math> | ||
| − | Let <math>\triangle ABC</math> be any | + | Let <math>\triangle ABC</math> be any isosceles triangle and let <math>\triangle A'B'C'</math> be its Gossard triangle. Then the lines <math>AA', BB',</math> and <math>CC'</math> are concurrent. We call the point of concurrence <math>Go</math> as the Gossard perspector of <math>\triangle ABC.</math> Let <math>H</math> be the orthocenter of <math>\triangle ABC, O</math> be the circumcenter of <math>\triangle ABC.</math> |
It is clear that <math>Go</math> is the midpoint of <math>AA'.</math> | It is clear that <math>Go</math> is the midpoint of <math>AA'.</math> | ||
| Line 41: | Line 47: | ||
<math>\triangle A'BM = \triangle CNA' \sim \triangle CBA</math> with coefficient <math>k = \frac {1}{2}.</math> | <math>\triangle A'BM = \triangle CNA' \sim \triangle CBA</math> with coefficient <math>k = \frac {1}{2}.</math> | ||
| − | Any | + | Any isosceles triangle and its Gossard triangle are congruent. |
| − | Any | + | Any isosceles triangle and its Gossard triangle have the same Euler line. |
| − | The Gossard triangle of the | + | The Gossard triangle of the isosceles <math>\triangle ABC</math> is the reflection of <math>\triangle ABC</math> in the Gossard perspector. |
Denote <math>\angle BAC = \alpha, \angle ABC = \angle ACB = \beta, AO = BO = R \implies</math> | Denote <math>\angle BAC = \alpha, \angle ABC = \angle ACB = \beta, AO = BO = R \implies</math> | ||
<cmath>\sin \beta = \cos \frac {\alpha}{2}, GoO = AO – AGo = R \cdot \frac{1 – \cos {\alpha}}{2},</cmath> | <cmath>\sin \beta = \cos \frac {\alpha}{2}, GoO = AO – AGo = R \cdot \frac{1 – \cos {\alpha}}{2},</cmath> | ||
| Line 51: | Line 57: | ||
'''vladimir.shelomovskii@gmail.com, vvsss''' | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
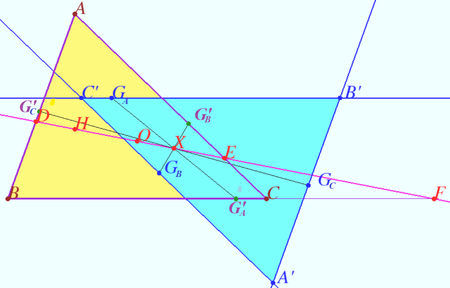
==Euler line of the triangle formed by the Euler line and the sides of a given triangle== | ==Euler line of the triangle formed by the Euler line and the sides of a given triangle== | ||
[[File:Euler Euler line.png|500px|right]] | [[File:Euler Euler line.png|500px|right]] | ||
| − | Let the Euler line of <math>\triangle ABC</math> meet the | + | Let the Euler line of <math>\triangle ABC</math> meet the lines <math>AB, AC,</math> and <math>BC</math> at <math>D, E,</math> and <math>F,</math> respectively. |
| + | |||
| + | Euler line of the <math>\triangle ADE</math> is parallel to <math>BC.</math> Similarly, Euler line of the <math>\triangle BDF</math> is parallel to <math>AC,</math> Euler line of the <math>\triangle CEF</math> is parallel to <math>AB.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Denote <math>\angle A = \alpha, \angle B = \beta, \angle C = \gamma,</math> smaller angles between the Euler line and lines <math>BC, AC,</math> and <math>AB</math> as <math>\theta_A, \theta_B,</math> and <math>\theta_C,</math> respectively. WLOG, <math>AC > BC > AB.</math> | ||
| + | It is known that <math>\tan \theta_A = \frac{3 – \tan \beta \cdot \tan \gamma}{\tan \beta – \tan \gamma}, \tan \theta_B = \frac{3 – \tan \alpha \cdot \tan \gamma}{\tan \alpha – \tan \gamma}, \tan \theta_C = \frac{3 – \tan \beta \cdot \tan \alpha}{\tan \beta – \tan \alpha}.</math> | ||
| + | *[[Euler line]] | ||
| + | Let <math>O'</math> be circumcenter of <math>\triangle ADE, KO'</math> be Euler line of <math>\triangle ADE, K \in DE</math> (line). | ||
| + | |||
| + | Similarly, <math>\tan \angle O'KF = \frac{3 – \tan \theta_B \cdot \tan \theta_C}{\tan \theta_C – \tan \theta_B}.</math> | ||
| + | <cmath>3(\tan\alpha – \tan \gamma) (\tan\alpha – \tan \beta) – (3 – \tan \alpha \cdot \tan \gamma) (3 – \tan \alpha \cdot \tan \beta) = (\tan^2 \alpha – 3) \cdot (3 –\tan \beta \cdot \tan \gamma),</cmath> | ||
| + | <cmath>(3 – \tan \alpha \cdot \tan \gamma) \cdot (\tan\alpha – \tan \beta) – (3 – \tan \alpha \cdot \tan \beta) \cdot (\tan\alpha – \tan \gamma) = (\tan^2 \alpha – 3) \cdot (\tan \beta – \tan \gamma).</cmath> | ||
| + | Suppose, <math>\tan^2 \alpha \ne 3</math> which means <math>\alpha \ne 60^\circ</math> and <math>\alpha \ne 120^\circ.</math> In this case | ||
| + | <cmath>\tan \angle O'KF = \frac{3 – \tan \beta \cdot \tan \gamma}{\tan \beta – \tan \gamma} = \tan \theta_A \implies \angle O'KF = \theta_A \implies O'K||BC.</cmath> | ||
| + | |||
| + | Similarly one can prove the claim in the other cases. | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Gossard triangle for triangle with angle 60== | ||
| + | [[File:Gossard 60.png|500px|right]] | ||
| + | Let <math>\angle A</math> of the triangle <math>ABC</math> be <math>60^\circ, \angle B \ne 60^\circ.</math> | ||
| + | Let the Euler line of <math>\triangle ABC</math> meet the lines <math>AB, AC</math> and <math>BC</math> at points <math>D, E,</math> and <math>F,</math> respectively. | ||
| + | Prove that <math>\triangle ADE</math> is an equilateral triangle. | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Denote <math>\angle ABC = \beta, \angle ACB = \gamma.</math> | ||
| + | It is known that <cmath>\tan \angle AED = \tan \theta_B = \frac{3 – \tan \alpha \cdot \tan \gamma}{\tan \alpha – \tan \gamma}.</cmath> | ||
| + | *[[Euler line]] | ||
| + | <cmath>\tan \angle AED = \frac{3 – \sqrt{3} \tan \gamma}{\sqrt{3} – \tan \gamma} = \sqrt{3} \implies \angle AED = 60^\circ.</cmath> | ||
| + | Therefore <math>\triangle ADE</math> is equilateral triangle. | ||
| + | |||
| + | Let <math>\triangle A'B'C'</math> be the triangle formed by the Euler lines of the <math>\triangle BDF, \triangle CEF,</math> and the line <math>l</math> contains centroid <math>G</math> of the <math>\triangle ADE</math> and parallel to <math>BC,</math> the vertex <math>B'</math> being the intersection of the Euler line of the <math>\triangle CEF</math> and <math>l,</math> the vertex <math>C'</math> being the intersection of the Euler line of the <math>\triangle BDF</math> and <math>l,</math> the vertex <math>A'</math> being the intersection of the Euler lines of the <math>\triangle BDF</math> and <math>\triangle CEF.</math> | ||
| + | |||
| + | We call the triangle <math>\triangle A'B'C'</math> as the Gossard triangle of the <math>\triangle ABC.</math> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | ==Gossard triangle for triangle with angle 120== | ||
| + | [[File:Gossard 120.png|500px|right]] | ||
| + | Let <math>\angle A</math> of the triangle <math>ABC</math> be <math>120^\circ, \angle B \ne 30^\circ.</math> | ||
| + | Let the Euler line of <math>\triangle ABC</math> meet the lines <math>AB, AC</math> and <math>BC</math> at points <math>D, E,</math> and <math>F,</math> respectively. Then <math>\triangle ADE</math> is an equilateral triangle. | ||
| + | |||
| + | One can prove this claim using the same formulae as in the case <math>\angle A = 60^\circ.</math> | ||
| + | |||
| + | Let <math>\triangle A'B'C'</math> be the triangle formed by the Euler lines of the <math>\triangle BDF, \triangle CEF,</math> and the line <math>l</math> contains centroid <math>G</math> of the <math>\triangle ADE</math> and parallel to <math>BC,</math> the vertex <math>B'</math> being the intersection of the Euler line of the <math>\triangle CEF</math> and <math>l,</math> the vertex <math>C'</math> being the intersection of the Euler line of the <math>\triangle BDF</math> and <math>l,</math> the vertex <math>A'</math> being the intersection of the Euler lines of the <math>\triangle BDF</math> and <math>\triangle CEF.</math> | ||
| + | |||
| + | We call the triangle <math>\triangle A'B'C'</math> as the Gossard triangle of the <math>\triangle ABC.</math> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
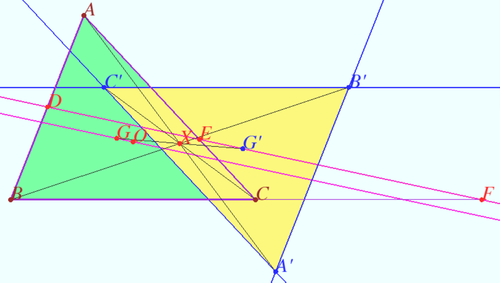
| + | ==Gossard perspector== | ||
| + | [[File:Gossard complete.png|450px|right]] | ||
| + | Let non equilateral triangle <math>ABC</math> be given. The Euler line of <math>\triangle ABC</math> crosses lines <math>AB, BC,</math> and <math>AC</math> at points <math>D, E,</math> and <math>F,</math> respectively. | ||
| + | |||
| + | Let the point <math>X</math> be the centroid of the set of points <math>A, B, C, D, E, F.</math> | ||
| + | |||
| + | Let Gossard triangle <math>A'B'C'</math> be defined as described above. | ||
| + | |||
| + | Prove that <math>\triangle A'B'C'</math> and <math>\triangle ABC</math> are homothetic and congruent, and the homothetic center is the point <math>X,</math> the Euler line of <math>\triangle A'B'C' </math> coincide with the Euler line of <math>\triangle ABC.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Denote <math>G_A, G_B,</math> and <math>G_C</math> centroids of the triangles <math>ADE, BDF,</math> and <math>CEF,</math> respectively. | ||
| + | It is clear that <math>G_A \in B'C', G_B \in A'C', G_C \in A'B', X \in</math> Euler line. | ||
| + | |||
| + | Let point <math>G'_A</math> be symmetric to the point <math>G_A</math> with respect to the point <math>X.</math> | ||
| + | |||
| + | Similarly we define points <math>G'_B</math> and <math>G'_C.</math> | ||
| + | <cmath>\vec {G'_A} = 2 \vec X – \vec G_A = \frac {\vec A+\vec B+\vec C+ \vec D+\vec E + \vec F}{3} – \frac {\vec A+ \vec D+\vec E }{3} = \frac {\vec B+\vec C+ \vec F}{3} \in BC.</cmath> | ||
| + | Similarly <math>G'_B \in AC</math> and <math>G'_C \in AB.</math> | ||
| + | |||
| + | <math>AB||A'B', AC || A'C', BC|| B'C' \implies</math> the crosspoints of lines <math>A'B', A'C',</math> and <math>B'C'</math> are symmetric to the crosspoints of lines <math>AB, AC,</math> and <math>BC,</math> therefore points <math>A', B',</math> and <math>C',</math> are symmetric to points <math>A, B,</math> and <math>C</math> with respect to the point <math>X \implies X</math> is the Gossard perspector of the <math>\triangle ABC.</math> | ||
| + | |||
| + | It is clear that the Gossard perspector lyes on Euler line of the <math>\triangle ABC</math> and <math>\triangle A'B'C'</math> is congruent to <math>\triangle ABC</math>. | ||
| + | |||
| + | The Euler line of <math>\triangle A'B'C'</math> is symmetric to the Euler line of <math>\triangle ABC</math> with respect to <math>X.</math> Therefore these lines coincide. | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Zeeman’s Generalisation== | ||
| + | [[File:Generalization 1.png|500px|right]] | ||
| + | Let <math>l</math> be any line parallel to the Euler line of non equilateral triangle <math>ABC.</math> Let <math>l</math> intersect the sidelines <math>AB, CA, BC</math> of <math>\triangle ABC</math> at points <math>D, E, F,</math> respectively. Let <math>\triangle A'B'C'</math> be the triangle formed by the Euler lines (as in previous sections) of the triangles <math>\triangle ADE, \triangle BDF,</math> and <math>\triangle CEF.</math> Let the point <math>X</math> be the centroid of the set of points <math>A, B, C, D, E, F.</math> | ||
| + | |||
| + | Then <math>\triangle A'B'C'</math> and <math>\triangle ABC</math> are homothetic and congruent, and the homothetic center is the point <math>X,</math> the Euler line of <math>\triangle A'B'C'</math> coincide with the line <math>DE</math> and the point <math>X</math> is equidistant from the Euler lines. | ||
| + | |||
| + | In this case <math>X</math> usually called the Zeeman–Gossard perspector. | ||
| + | |||
| + | One can prove this claim using the method of previous section. | ||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
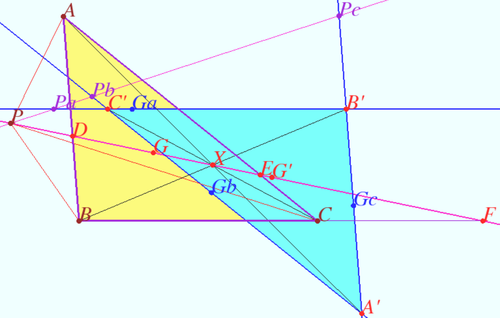
| + | ==Paul Yiu's Generalization== | ||
| + | [[File:Yu generalization.png|500px|right]] | ||
| + | Let <math>P</math> be any point in the plane of non equilateral triangle <math>ABC</math> different from its centroid <math>G.</math> | ||
| + | |||
| + | Let the line <math>PG</math> meet the sidelines <math>AB, CA,</math> and <math>BC</math> at <math>D, E,</math> and <math>D,</math> respectively. | ||
| + | |||
| + | Let the centroids of the triangles <math>AED, BDF,</math> and <math>CFE</math> be <math>Ga, Gb,</math> and <math>Gc,</math> respectively. | ||
| + | |||
| + | Let <math>Pa</math> be a point such that <math>EPa</math> is parallel to <math>CP</math> and <math>DPa</math> is parallel to <math>BP.</math> | ||
| + | Symilarly, <math>Pb: DPb||AP, FPb||CP, Pc: FPc||BP, EPc||AP.</math> | ||
| + | |||
| + | Let <math>\triangle A'B'C'</math> be the triangle formed by the lines <math>GaPa, GbPb,</math> and <math>GcPc.</math> | ||
| + | Let the point <math>X</math> be the centroid of the set of points <math>A, B, C, D, E, F.</math> | ||
| + | Then <math>\triangle A'B'C'</math> and <math>\triangle ABC</math> are homothetic and congruent, and the homothetic center is the point <math>X,</math> the points <math>P, G,</math> and <math>G'</math> are collinear. | ||
| + | |||
| + | One can prove this claim using the method of previous section. | ||
| + | |||
| + | The points <math>P, Pa, Pb,</math> and <math>Pc</math> are collinear. | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | == Dao Thanh Oai's Generalization== | ||
| + | [[File:Generalization.png|400px|right]] | ||
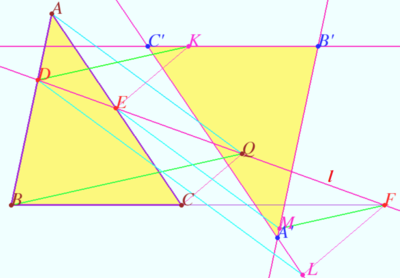
| + | Let triangle <math>ABC</math> and line <math>\ell,</math> non parallel to sidelines be given. Let line <math>\ell</math> meets sidelines <math>AB, AC, BC</math> of <math>\triangle ABC</math> at points <math>D, E, F,</math> respectively. | ||
| + | |||
| + | Let <math>Q \in \ell.</math> Let <math>K, L, M</math> be the points such that <math>QA||EM||DL, QB||KD||FM, QC||KE||FL.</math> | ||
| + | |||
| + | Similarly define points <math>P \in \ell, K_0, L_0, M_0.</math> | ||
| + | |||
| + | Let triangle <math>\triangle A'B'C'</math> be the triangle formed by the lines <math>KK_0, LL_0, MM_0.</math> | ||
| + | |||
| + | Prove that <math>\triangle A'B'C'</math> and <math>\triangle ABC</math> are homothetic and congruent, and the homothetic center lies on <math>\ell.</math> | ||
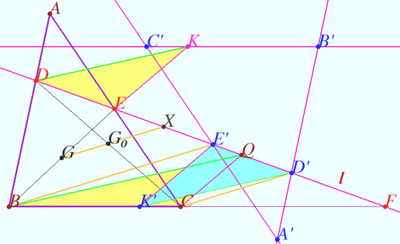
<i><b>Proof</b></i> | <i><b>Proof</b></i> | ||
| + | [[File:Dao Generalization.png|400px|right]] | ||
| + | Let <math>G</math> and <math>G_0</math> be the midpoints <math>BE</math> and <math>CD,</math> respectively. | ||
| + | |||
| + | Let <math>X</math> be the crosspoint of <math>\ell</math> and Gauss line <math>GG_0.</math> | ||
| + | |||
| + | Let <math>A', B', C', D', E',</math> and <math>K'</math> be the points simmetric to <math>A, B, C, D, E,</math> and <math>K</math> with respect to <math>X,</math> respectively. | ||
| + | |||
| + | We will prove that <math>K' \in BC</math> which means that <math>K \in B'C' \implies K_0 \in BC, L \in AC</math> and so on. | ||
| + | |||
| + | <math>G</math> midpoint <math>BE, X</math> midpoint <math>EE' \implies GX||BE'.</math> | ||
| + | |||
| + | <math>G_0</math> midpoint <math>DC, X</math> midpoint <math>DD' \implies G_0X||CD' \implies BE'||CD'.</math> | ||
| + | <math>KD||K'D'||BQ, KE||K'E'||CQ, CD'||BE', Q \in D'E' \implies K' \in BC</math> according the Claim. | ||
| + | |||
| + | <i><b>Claim (Parallel lines in trapezium)</b></i> | ||
| + | [[File:Pappus.png|300px|right]] | ||
| + | [[File:Pappus non convex.png|300px|right]] | ||
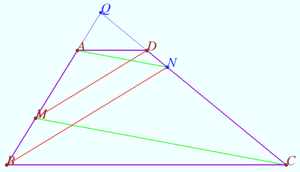
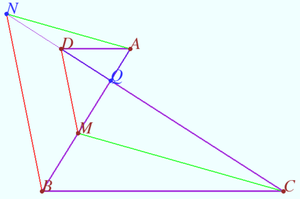
| + | Let <math>ABCD</math> be the quadrungle such that <math>AD||BC.</math> | ||
| + | Let <math>M \in AB, MD||BN, AN||CM.</math> | ||
| + | Prove that point <math>N</math> lyes on <math>CD.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | We prove Claim in the case <math>AB</math> non parallel to <math>CD.</math> | ||
| + | Denote <math>Q = AB \cap CD.</math> | ||
| + | |||
| + | <math>AD||BC \implies \frac {QB}{QA}= \frac{QC}{QD}.</math> | ||
| + | |||
| + | Let <math>BN||MD</math> cross <math>CD</math> at <math>N.</math> Then <math>\frac {QN}{QD}=\frac {QB}{QM}.</math> | ||
| + | |||
| + | <cmath>\frac {QC}{QN} = \frac {QC}{QD} \cdot \frac {QD}{QN} = \frac {QB}{QA} \cdot \frac {QM}{QB} = \frac {QM}{QA} \implies AN||CM.</cmath> | ||
| + | The Claim is correct in the case of non convex <math>ABCD.</math> One can simplify the proof of Dao Generalization using this variant of the Claim. | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
Latest revision as of 05:44, 19 January 2023
Contents
- 1 Gossard perspector X(402) and Gossard triangle
- 2 Gossard perspector of right triangle
- 3 Gossard perspector and Gossard triangle for isosceles triangle
- 4 Euler line of the triangle formed by the Euler line and the sides of a given triangle
- 5 Gossard triangle for triangle with angle 60
- 6 Gossard triangle for triangle with angle 120
- 7 Gossard perspector
- 8 Zeeman’s Generalisation
- 9 Paul Yiu's Generalization
- 10 Dao Thanh Oai's Generalization
Gossard perspector X(402) and Gossard triangle
In ![]() Leonhard Euler proved that in any triangle, the orthocenter, circumcenter and centroid are collinear. We name this line the Euler line. Soon he proved that the Euler line of a given triangle together with two of its sides forms a triangle whose Euler line is in parallel with the third side of the given triangle.
Leonhard Euler proved that in any triangle, the orthocenter, circumcenter and centroid are collinear. We name this line the Euler line. Soon he proved that the Euler line of a given triangle together with two of its sides forms a triangle whose Euler line is in parallel with the third side of the given triangle.
Professor Harry Clinton Gossard in ![]() proved that three Euler lines of the triangles formed by the Euler line and the sides, taken by two, of a given triangle, form a triangle which is perspective with the given triangle and has the same Euler line. The center of the perspective now is known as the Gossard perspector or the Kimberling point
proved that three Euler lines of the triangles formed by the Euler line and the sides, taken by two, of a given triangle, form a triangle which is perspective with the given triangle and has the same Euler line. The center of the perspective now is known as the Gossard perspector or the Kimberling point ![]() It is the crosspoint of Gauss line and Euler line.
It is the crosspoint of Gauss line and Euler line.
Let triangle ![]() be given. The Euler line crosses lines
be given. The Euler line crosses lines ![]() and
and ![]() at points
at points ![]() and
and ![]()
On ![]() it was found that the Gossard perspector is the centroid of the points
it was found that the Gossard perspector is the centroid of the points ![]()
vladimir.shelomovskii@gmail.com, vvsss
Gossard perspector of right triangle
It is clear that the Euler line of right triangle ![]() meet the sidelines
meet the sidelines ![]() and
and ![]() of
of ![]() at
at ![]() and
and ![]() where
where ![]() is the midpoint of
is the midpoint of ![]()
Let ![]() be the triangle formed by the Euler lines of the
be the triangle formed by the Euler lines of the ![]() and the line
and the line ![]() contains
contains ![]() and parallel to
and parallel to ![]() the vertex
the vertex ![]() being the intersection of the Euler line of the
being the intersection of the Euler line of the ![]() and
and ![]() the vertex
the vertex ![]() being the intersection of the Euler line of the
being the intersection of the Euler line of the ![]() and
and ![]()
We call the triangle ![]() as the Gossard triangle of
as the Gossard triangle of ![]()
Let ![]() be any right triangle and let
be any right triangle and let ![]() be its Gossard triangle. Then the lines
be its Gossard triangle. Then the lines ![]() and
and ![]() are concurrent. We call the point of concurrence
are concurrent. We call the point of concurrence ![]() as the Gossard perspector of
as the Gossard perspector of ![]()
![]() is the midpoint of
is the midpoint of ![]()
![]() is orthocenter of
is orthocenter of ![]() is circumcenter of
is circumcenter of ![]() so
so ![]() is midpoint of
is midpoint of ![]()
![]() is the midpoint
is the midpoint ![]() is the midpoint
is the midpoint ![]() with coefficient
with coefficient ![]()
Any right triangle and its Gossard triangle are congruent.
Any right triangle and its Gossard triangle have the same Euler line.
The Gossard triangle of the right ![]() is the reflection of
is the reflection of ![]() in the Gossard perspector.
in the Gossard perspector.
vladimir.shelomovskii@gmail.com, vvsss
Gossard perspector and Gossard triangle for isosceles triangle
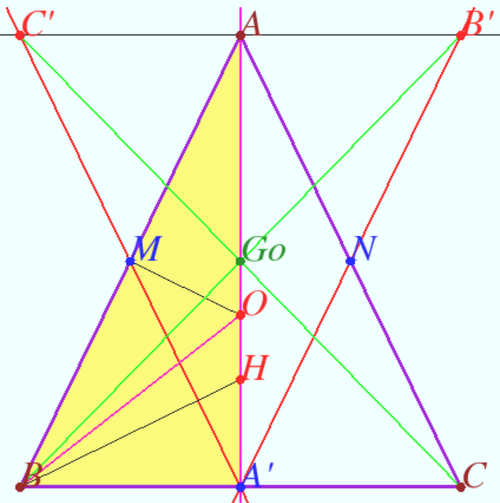
It is clear that the Euler line of isosceles ![]() meet the sidelines
meet the sidelines ![]() and
and ![]() of
of ![]() at
at ![]() and
and ![]() where
where ![]() is the midpoint of
is the midpoint of ![]()
Let ![]() be the triangle formed by the Euler lines of the
be the triangle formed by the Euler lines of the ![]() and the line
and the line ![]() contains
contains ![]() and parallel to
and parallel to ![]() the vertex
the vertex ![]() being the intersection of the Euler line of the
being the intersection of the Euler line of the ![]() and
and ![]() the vertex
the vertex ![]() being the intersection of the Euler line of the
being the intersection of the Euler line of the ![]() and
and ![]()
We call the triangle ![]() as the Gossard triangle of
as the Gossard triangle of ![]()
Let ![]() be any isosceles triangle and let
be any isosceles triangle and let ![]() be its Gossard triangle. Then the lines
be its Gossard triangle. Then the lines ![]() and
and ![]() are concurrent. We call the point of concurrence
are concurrent. We call the point of concurrence ![]() as the Gossard perspector of
as the Gossard perspector of ![]() Let
Let ![]() be the orthocenter of
be the orthocenter of ![]() be the circumcenter of
be the circumcenter of ![]()
It is clear that ![]() is the midpoint of
is the midpoint of ![]()
![]() is the midpoint
is the midpoint ![]() is the midpoint
is the midpoint ![]()
![]() with coefficient
with coefficient ![]()
Any isosceles triangle and its Gossard triangle are congruent.
Any isosceles triangle and its Gossard triangle have the same Euler line.
The Gossard triangle of the isosceles ![]() is the reflection of
is the reflection of ![]() in the Gossard perspector.
Denote
in the Gossard perspector.
Denote ![]()
![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss
Euler line of the triangle formed by the Euler line and the sides of a given triangle
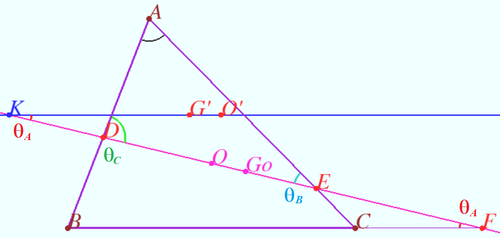
Let the Euler line of ![]() meet the lines
meet the lines ![]() and
and ![]() at
at ![]() and
and ![]() respectively.
respectively.
Euler line of the ![]() is parallel to
is parallel to ![]() Similarly, Euler line of the
Similarly, Euler line of the ![]() is parallel to
is parallel to ![]() Euler line of the
Euler line of the ![]() is parallel to
is parallel to ![]()
Proof
Denote ![]() smaller angles between the Euler line and lines
smaller angles between the Euler line and lines ![]() and
and ![]() as
as ![]() and
and ![]() respectively. WLOG,
respectively. WLOG, ![]() It is known that
It is known that ![]()
Let ![]() be circumcenter of
be circumcenter of ![]() be Euler line of
be Euler line of ![]() (line).
(line).
Similarly, ![]()
![]()
![]() Suppose,
Suppose, ![]() which means
which means ![]() and
and ![]() In this case
In this case
![]()
Similarly one can prove the claim in the other cases.
vladimir.shelomovskii@gmail.com, vvsss
Gossard triangle for triangle with angle 60
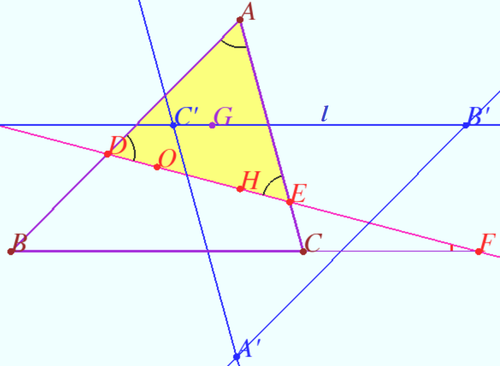
Let ![]() of the triangle
of the triangle ![]() be
be ![]() Let the Euler line of
Let the Euler line of ![]() meet the lines
meet the lines ![]() and
and ![]() at points
at points ![]() and
and ![]() respectively.
Prove that
respectively.
Prove that ![]() is an equilateral triangle.
is an equilateral triangle.
Proof
Denote ![]() It is known that
It is known that ![]()
![]() Therefore
Therefore ![]() is equilateral triangle.
is equilateral triangle.
Let ![]() be the triangle formed by the Euler lines of the
be the triangle formed by the Euler lines of the ![]() and the line
and the line ![]() contains centroid
contains centroid ![]() of the
of the ![]() and parallel to
and parallel to ![]() the vertex
the vertex ![]() being the intersection of the Euler line of the
being the intersection of the Euler line of the ![]() and
and ![]() the vertex
the vertex ![]() being the intersection of the Euler line of the
being the intersection of the Euler line of the ![]() and
and ![]() the vertex
the vertex ![]() being the intersection of the Euler lines of the
being the intersection of the Euler lines of the ![]() and
and ![]()
We call the triangle ![]() as the Gossard triangle of the
as the Gossard triangle of the ![]()
vladimir.shelomovskii@gmail.com, vvsss
Gossard triangle for triangle with angle 120
Let ![]() of the triangle
of the triangle ![]() be
be ![]() Let the Euler line of
Let the Euler line of ![]() meet the lines
meet the lines ![]() and
and ![]() at points
at points ![]() and
and ![]() respectively. Then
respectively. Then ![]() is an equilateral triangle.
is an equilateral triangle.
One can prove this claim using the same formulae as in the case ![]()
Let ![]() be the triangle formed by the Euler lines of the
be the triangle formed by the Euler lines of the ![]() and the line
and the line ![]() contains centroid
contains centroid ![]() of the
of the ![]() and parallel to
and parallel to ![]() the vertex
the vertex ![]() being the intersection of the Euler line of the
being the intersection of the Euler line of the ![]() and
and ![]() the vertex
the vertex ![]() being the intersection of the Euler line of the
being the intersection of the Euler line of the ![]() and
and ![]() the vertex
the vertex ![]() being the intersection of the Euler lines of the
being the intersection of the Euler lines of the ![]() and
and ![]()
We call the triangle ![]() as the Gossard triangle of the
as the Gossard triangle of the ![]()
vladimir.shelomovskii@gmail.com, vvsss
Gossard perspector
Let non equilateral triangle ![]() be given. The Euler line of
be given. The Euler line of ![]() crosses lines
crosses lines ![]() and
and ![]() at points
at points ![]() and
and ![]() respectively.
respectively.
Let the point ![]() be the centroid of the set of points
be the centroid of the set of points ![]()
Let Gossard triangle ![]() be defined as described above.
be defined as described above.
Prove that ![]() and
and ![]() are homothetic and congruent, and the homothetic center is the point
are homothetic and congruent, and the homothetic center is the point ![]() the Euler line of
the Euler line of ![]() coincide with the Euler line of
coincide with the Euler line of ![]()
Proof
Denote ![]() and
and ![]() centroids of the triangles
centroids of the triangles ![]() and
and ![]() respectively.
It is clear that
respectively.
It is clear that ![]() Euler line.
Euler line.
Let point ![]() be symmetric to the point
be symmetric to the point ![]() with respect to the point
with respect to the point ![]()
Similarly we define points ![]() and
and ![]()
![]() Similarly
Similarly ![]() and
and ![]()
![]() the crosspoints of lines
the crosspoints of lines ![]() and
and ![]() are symmetric to the crosspoints of lines
are symmetric to the crosspoints of lines ![]() and
and ![]() therefore points
therefore points ![]() and
and ![]() are symmetric to points
are symmetric to points ![]() and
and ![]() with respect to the point
with respect to the point ![]() is the Gossard perspector of the
is the Gossard perspector of the ![]()
It is clear that the Gossard perspector lyes on Euler line of the ![]() and
and ![]() is congruent to
is congruent to ![]() .
.
The Euler line of ![]() is symmetric to the Euler line of
is symmetric to the Euler line of ![]() with respect to
with respect to ![]() Therefore these lines coincide.
Therefore these lines coincide.
vladimir.shelomovskii@gmail.com, vvsss
Zeeman’s Generalisation
Let ![]() be any line parallel to the Euler line of non equilateral triangle
be any line parallel to the Euler line of non equilateral triangle ![]() Let
Let ![]() intersect the sidelines
intersect the sidelines ![]() of
of ![]() at points
at points ![]() respectively. Let
respectively. Let ![]() be the triangle formed by the Euler lines (as in previous sections) of the triangles
be the triangle formed by the Euler lines (as in previous sections) of the triangles ![]() and
and ![]() Let the point
Let the point ![]() be the centroid of the set of points
be the centroid of the set of points ![]()
Then ![]() and
and ![]() are homothetic and congruent, and the homothetic center is the point
are homothetic and congruent, and the homothetic center is the point ![]() the Euler line of
the Euler line of ![]() coincide with the line
coincide with the line ![]() and the point
and the point ![]() is equidistant from the Euler lines.
is equidistant from the Euler lines.
In this case ![]() usually called the Zeeman–Gossard perspector.
usually called the Zeeman–Gossard perspector.
One can prove this claim using the method of previous section. vladimir.shelomovskii@gmail.com, vvsss
Paul Yiu's Generalization
Let ![]() be any point in the plane of non equilateral triangle
be any point in the plane of non equilateral triangle ![]() different from its centroid
different from its centroid ![]()
Let the line ![]() meet the sidelines
meet the sidelines ![]() and
and ![]() at
at ![]() and
and ![]() respectively.
respectively.
Let the centroids of the triangles ![]() and
and ![]() be
be ![]() and
and ![]() respectively.
respectively.
Let ![]() be a point such that
be a point such that ![]() is parallel to
is parallel to ![]() and
and ![]() is parallel to
is parallel to ![]() Symilarly,
Symilarly, ![]()
Let ![]() be the triangle formed by the lines
be the triangle formed by the lines ![]() and
and ![]() Let the point
Let the point ![]() be the centroid of the set of points
be the centroid of the set of points ![]() Then
Then ![]() and
and ![]() are homothetic and congruent, and the homothetic center is the point
are homothetic and congruent, and the homothetic center is the point ![]() the points
the points ![]() and
and ![]() are collinear.
are collinear.
One can prove this claim using the method of previous section.
The points ![]() and
and ![]() are collinear.
are collinear.
vladimir.shelomovskii@gmail.com, vvsss
Dao Thanh Oai's Generalization
Let triangle ![]() and line
and line ![]() non parallel to sidelines be given. Let line
non parallel to sidelines be given. Let line ![]() meets sidelines
meets sidelines ![]() of
of ![]() at points
at points ![]() respectively.
respectively.
Let ![]() Let
Let ![]() be the points such that
be the points such that ![]()
Similarly define points ![]()
Let triangle ![]() be the triangle formed by the lines
be the triangle formed by the lines ![]()
Prove that ![]() and
and ![]() are homothetic and congruent, and the homothetic center lies on
are homothetic and congruent, and the homothetic center lies on ![]()
Proof
Let ![]() and
and ![]() be the midpoints
be the midpoints ![]() and
and ![]() respectively.
respectively.
Let ![]() be the crosspoint of
be the crosspoint of ![]() and Gauss line
and Gauss line ![]()
Let ![]() and
and ![]() be the points simmetric to
be the points simmetric to ![]() and
and ![]() with respect to
with respect to ![]() respectively.
respectively.
We will prove that ![]() which means that
which means that ![]() and so on.
and so on.
![]() midpoint
midpoint ![]() midpoint
midpoint ![]()
![]() midpoint
midpoint ![]() midpoint
midpoint ![]()
![]() according the Claim.
according the Claim.
Claim (Parallel lines in trapezium)
Let ![]() be the quadrungle such that
be the quadrungle such that ![]() Let
Let ![]() Prove that point
Prove that point ![]() lyes on
lyes on ![]()
Proof
We prove Claim in the case ![]() non parallel to
non parallel to ![]() Denote
Denote ![]()
![]()
Let ![]() cross
cross ![]() at
at ![]() Then
Then ![]()
![]() The Claim is correct in the case of non convex
The Claim is correct in the case of non convex ![]() One can simplify the proof of Dao Generalization using this variant of the Claim.
One can simplify the proof of Dao Generalization using this variant of the Claim.
vladimir.shelomovskii@gmail.com, vvsss