Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Spieker center"

(→‎Nagel line)
(→‎Shatunov triangle)
 
(3 intermediate revisions by the same user not shown)
Line 79: Line 79:
 
'''vladimir.shelomovskii@gmail.com, vvsss'''
 
'''vladimir.shelomovskii@gmail.com, vvsss'''
 
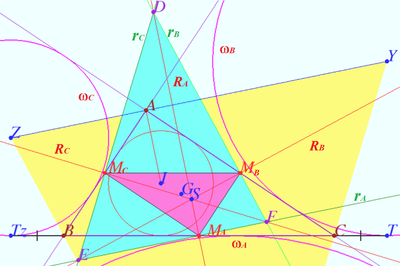
==Shatunov triangle==
 
==Shatunov triangle==
−
[[File:Shatunov triangle.png|400px|right]]
+
[[File:Shatunov triangle A.png|400px|right]]
 
Let <math>\triangle ABC</math> be given. Let <math>\omega, \omega_A, \omega_B, \omega_C</math> be incircle, A-excircle, B-excircle, C-excircle centered at points <math>I,X,Y,Z,</math> respectively.
 
Let <math>\triangle ABC</math> be given. Let <math>\omega, \omega_A, \omega_B, \omega_C</math> be incircle, A-excircle, B-excircle, C-excircle centered at points <math>I,X,Y,Z,</math> respectively.
  
Line 95: Line 95:
  
 
a) Let <math>M_A, M_B, M_C</math> be the midpoints of <math>BC, AC, AB,</math> respectively.
 
a) Let <math>M_A, M_B, M_C</math> be the midpoints of <math>BC, AC, AB,</math> respectively.
 +
 +
The distances from <math>M_A</math> to the tangent points of <math>\omega</math> and <math>\omega_A</math> are the same, so <math>M_A \in r_A.</math> Similarly <math>M_B \in r_B, M_C \in r_C.</math>
 +
 +
Let <math>T</math> and <math>T_Z</math> be the points of tangency of <math>BC</math> and <math>\omega_B</math> and <math>\omega_C,</math> respectively.
 +
 +
It is clear that <math>TC = BT_Z, BM_A = CM_A \implies M_A</math> lies on the radical axis <math>R_A.</math>
 +
 +
Similarly, <math>M_B</math> lies on the radical axis <math>R_B, M_C</math> lies on the radical axis <math>R_C.</math>
 +
 
 +
<math>D = r_B \cap r_C  \implies</math> D is the radical center of <math>\omega, \omega_B, \omega_C \implies D \in R_A \implies R_A = DM_A.</math>
 +
 +
<math>AI \perp ZY, R_A \perp ZY, r_A \perp AI \implies  DM_A \perp EF.</math> Similarly <math>EM_B \perp DF, FM_C \perp DE.</math>
 +
 +
Therefore <math>DM_A, EM_B, FM_C</math> are the heights of <math>\triangle DEF \implies S</math> is the orthocenter of <math>\triangle DEF.</math>
 +
 +
<math>\triangle M_AM_BM_C</math> is the medial triangle of <math>\triangle ABC, DSM_A</math>
 +
is the bisector of <math>\angle M_BM_AM_C \implies S</math> is the Steiner point of <math>\triangle ABC.</math>
 +
 +
b) <math>ZY || EF, XY || ED, ZX || FD \implies \triangle DEF \sim \triangle XYZ.</math>
 +
 +
<math>I</math> is the orthocenter of <math>\triangle XYZ, S</math> is the orthocenter of <math>\triangle DEF.</math>
 +
 +
Points <math>I, G,</math> and <math>S,</math> where <math>G</math> is the centroid <math>ABC,</math>  are collinear,  sides of is the <math>\triangle DEF</math> are parallel to the respective sides of <math>\triangle XYZ \implies \triangle DEF</math> is homothetic to the <math>\triangle XYZ</math> with respect to <math>G.</math>
 +
 +
<math>IG = 2CS \implies</math> the coefficient of homothety is <math>\frac {1}{2}.</math>
 +
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''

Latest revision as of 05:48, 8 August 2023

The Spieker center is defined as the center of mass of the perimeter of the triangle. The Spieker center of a $\triangle ABC$ is the center of gravity of a homogeneous wire frame in the shape of $\triangle ABC.$ The Spieker center is a triangle center and it is listed as the point $X_{10}.$

Incenter of medial triangle

Physical proof.png

Prove that the Spieker center of triangle $\triangle ABC$ is the incenter of the medial triangle $\triangle DEF$ of a $\triangle ABC.$

Proof

Let's hang up the $\triangle ABC$ in the middle of side $BC.$ Side $BC$ is balanced.

Let's replace side $AC$ with point $E$ (the center of mass of $AC,$ the midpoint $AC).$ Denote $\rho$ the linear density of a homogeneous wire frame.

The mass of point $E$ is equal to $\rho \cdot AC,$ the shoulder of the gravity force is $EE' = ED \sin \alpha = \frac {AB \sin \alpha }{2}.$

The moment of this force is $g EE' \rho \cdot AC = \frac {g \rho\cdot AC \cdot AB}{2} \sin \alpha.$

Similarly the moment gravity force acting on AB is $\frac {g \rho\cdot AC \cdot AB}{2} \sin \beta.$

Therefore, equilibrium condition is $\alpha = \beta$ and the center of gravity of a homogeneous wire frame $ABC$ lies on each bisector of $\triangle DEF.$

This point is the incenter of the medial triangle $\triangle DEF.$

vladimir.shelomovskii@gmail.com, vvsss

Intersection of three cleavers

Cleaver.png

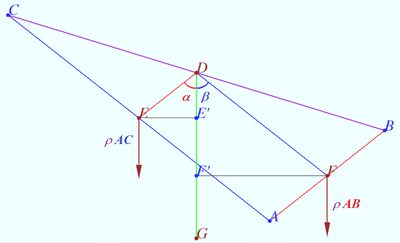
Prove that the Spieker center is located at the intersection of the three cleavers of triangle. A cleaver of a triangle is a line segment that bisects the perimeter of the triangle and has one endpoint at the midpoint of one of the three sides.

Proof

We use notation of previous proof. $DG$ is the segment contains the Spieker center, $G \in AB, \angle EDG = \angle FDG, H = DG \cap AC.$ WLOG, $AC > AB.$ \[DF||AC \implies \angle AHG = \angle FDG.\] Similarly, $\angle AGH = \angle EDG = \angle AHG.$

So $AH = AG \implies CH = AB + AH \implies DH$ is cleaver.

Therefore, the three cleavers meet at the Spieker center.

vladimir.shelomovskii@gmail.com, vvsss

Radical center of excircles

Radical center.png

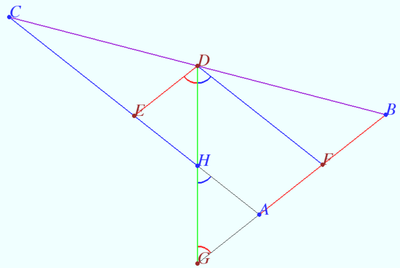
Prove that the Spieker center of triangle is the radical center of the three excircles.

Proof

Let $\triangle ABC$ be given,$M_A, M_B, M_C$ be the midpoints of $BC, AC, BC,$ respectively.

Let $\omega_A, \omega_B, \omega_C$ be A-excircle, B-excircle, C-excircle centered at $X,Y,Z,$ respectively.

Let $I$ be the incenter of $\triangle ABC.$ Let $R_A$ be the radical axis of $\omega_B$ and $\omega_C, R_B$ be the radical axis of $\omega_A$ and $\omega_C, R_C$ be the radical axis of $\omega_B$ and $\omega_A,$ respectively.

It is known that the distances from $B$ to the tangent points of $\omega_C$ is equal to the distances from $C$ to the tangent points of $\omega_B, BM_A = CM_A$ therefore $M_A$ lies on the radical axis $R_A$ of $\omega_B$ and $\omega_C.$ Similarly, $M_B \in R_B, M_C \in R_C.$

$AI \perp ZY, R_A \perp XY \implies AI || RA \implies R_A$ is cleaver. Similarly, $R_B$ and $R_C$ are cleavers.

Therefore the radical center of the three excircles coinside with the intersection of the three cleavers of triangle.

vladimir.shelomovskii@gmail.com, vvsss

Nagel line

Nagel line.png

Let points $I, G, S$ be the incenter, the centroid and the Spieker center of triangle $\triangle ABC,$ respectively. Prove that points $I, G, S$ are collinear, $IG = 2 GS,$ and the barycentric coordinates of S are ${ b+c : c+a : a+b.}$

The Nagel line is the line on which points $I, G, S,$ and Nagel point $N$ lie.

Proof

Let $D, E, F$ be the midpoints of $BC, AC, BC,$ respectively. Bisector $AI$ is parallel to cleaver $DS, BI || ES.$ \[AB ||ED, \frac {AB}{DE} = 2 \implies \triangle ABI \sim \triangle DES \implies \frac {AI}{DS} = 2.\] Centroid $G$ divide the median $AD$ such that $\frac {AG}{DG} = 2 \implies$

$\triangle AGI \sim \triangle DGS \implies \frac {GI}{SG} = 2,$ and points $I, G, S$ are collinear.

The barycentric coordinates of $I$ are ${a : b : c}.$ The barycentric coordinates of $G$ are ${1 : 1 : 1}.$

\[\vec {GI} = 2 \vec {SG} \implies \vec {G} - \vec {I} = 2(\vec {S} - \vec {G}) \implies\] \[\vec {G} = \frac {3 \vec {G} - \vec {I} }{2} = {1 - \frac{a}{a+ b+c} : 1 - \frac {b}{a+b+c} : 1 - \frac{c}{a+b+c}} = { b+c : c+a : a+b.}\]

vladimir.shelomovskii@gmail.com, vvsss

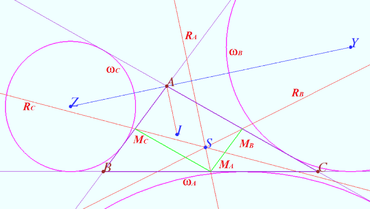
Shatunov triangle

Shatunov triangle A.png

Let $\triangle ABC$ be given. Let $\omega, \omega_A, \omega_B, \omega_C$ be incircle, A-excircle, B-excircle, C-excircle centered at points $I,X,Y,Z,$ respectively.

Let $r_A = EF, r_B = DF, r_C = DE$ be the radical axes of the inscribed circle and one of the excircles of $\triangle ABC.$

The triangle $\triangle DEF$ whose sides are $r_A, r_B, r_C$ we name the Shatunov triangle. Accordingly, the vertices of the Shatunov triangle are the radical centers of a pair of excircles and an inscribed circle.

Prove:

a) the heights of the Shatunov triangle lie on the bisectors of the medial triangle. The orthocenter of the Shatunov triangle is the Steiner point of $\triangle ABC.$

b) The Shatunov triangle is homothetic to the anticomplementary triangle of $\triangle ABC$ with respect to the centroid $ABC$ with coefficient $\frac {1}{2}.$

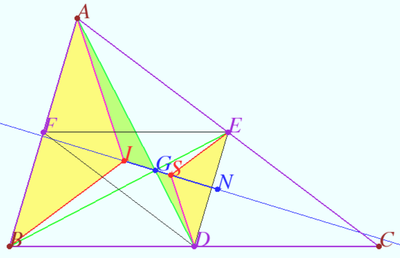
Proof

a) Let $M_A, M_B, M_C$ be the midpoints of $BC, AC, AB,$ respectively.

The distances from $M_A$ to the tangent points of $\omega$ and $\omega_A$ are the same, so $M_A \in r_A.$ Similarly $M_B \in r_B, M_C \in r_C.$

Let $T$ and $T_Z$ be the points of tangency of $BC$ and $\omega_B$ and $\omega_C,$ respectively.

It is clear that $TC = BT_Z, BM_A = CM_A \implies M_A$ lies on the radical axis $R_A.$

Similarly, $M_B$ lies on the radical axis $R_B, M_C$ lies on the radical axis $R_C.$

$D = r_B \cap r_C \implies$ D is the radical center of $\omega, \omega_B, \omega_C \implies D \in R_A \implies R_A = DM_A.$

$AI \perp ZY, R_A \perp ZY, r_A \perp AI \implies DM_A \perp EF.$ Similarly $EM_B \perp DF, FM_C \perp DE.$

Therefore $DM_A, EM_B, FM_C$ are the heights of $\triangle DEF \implies S$ is the orthocenter of $\triangle DEF.$

$\triangle M_AM_BM_C$ is the medial triangle of $\triangle ABC, DSM_A$ is the bisector of $\angle M_BM_AM_C \implies S$ is the Steiner point of $\triangle ABC.$

b) $ZY || EF, XY || ED, ZX || FD \implies \triangle DEF \sim \triangle XYZ.$

$I$ is the orthocenter of $\triangle XYZ, S$ is the orthocenter of $\triangle DEF.$

Points $I, G,$ and $S,$ where $G$ is the centroid $ABC,$ are collinear, sides of is the $\triangle DEF$ are parallel to the respective sides of $\triangle XYZ \implies \triangle DEF$ is homothetic to the $\triangle XYZ$ with respect to $G.$

$IG = 2CS \implies$ the coefficient of homothety is $\frac {1}{2}.$

vladimir.shelomovskii@gmail.com, vvsss

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Spieker_center&oldid=196628"