Difference between revisions of "2021 AIME I Problems/Problem 6"

Latest revision as of 23:50, 11 January 2024

Problem

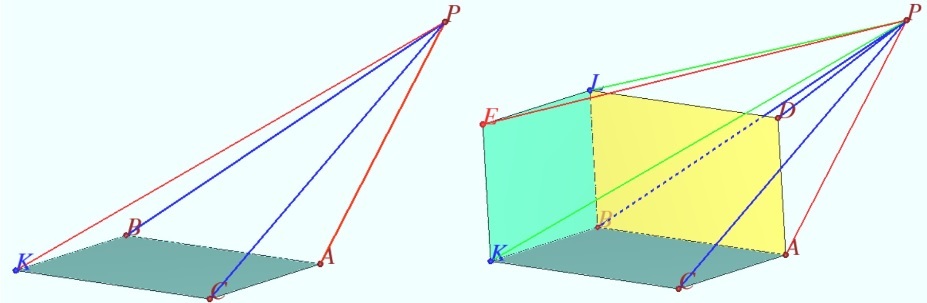
Segments $\overline{AB}, \overline{AC},$ and $\overline{AD}$ are edges of a cube and $\overline{AG}$ is a diagonal through the center of the cube. Point $P$ satisfies $BP=60\sqrt{10}$ , $CP=60\sqrt{5}$ , $DP=120\sqrt{2}$ , and $GP=36\sqrt{7}$ . Find $AP.$

Solution 1

First scale down the whole cube by $12$ . Let point $P$ have coordinates $(x, y, z)$ , point $A$ have coordinates $(0, 0, 0)$ , and $s$ be the side length. Then we have the equations $\begin{align*} (s-x)^2+y^2+z^2&=\left(5\sqrt{10}\right)^2, \\ x^2+(s-y)^2+z^2&=\left(5\sqrt{5}\right)^2, \\ x^2+y^2+(s-z)^2&=\left(10\sqrt{2}\right)^2, \\ (s-x)^2+(s-y)^2+(s-z)^2&=\left(3\sqrt{7}\right)^2. \end{align*}$ These simplify into $\begin{align*} s^2+x^2+y^2+z^2-2sx&=250, \\ s^2+x^2+y^2+z^2-2sy&=125, \\ s^2+x^2+y^2+z^2-2sz&=200, \\ 3s^2-2s(x+y+z)+x^2+y^2+z^2&=63. \end{align*}$ Adding the first three equations together, we get $3s^2-2s(x+y+z)+3(x^2+y^2+z^2)=575$ . Subtracting this from the fourth equation, we get $2(x^2+y^2+z^2)=512$ , so $x^2+y^2+z^2=256$ . This means $PA=16$ . However, we scaled down everything by $12$ so our answer is $16*12=\boxed{192}$ .

~JHawk0224

Solution 2 (Solution 1 with Slight Simplification)

Once the equations for the distance between point P and the vertices of the cube have been written, we can add the first, second, and third to receive, $2(x^2 + y^2 + z^2) + (s-x)^2 + (s-y)^2 + (s-z)^2 = 250 + 125 + 200.$ Subtracting the fourth equation gives $\begin{align*} 2(x^2 + y^2 + z^2) &= 575 - 63 \\ x^2 + y^2 + z^2 &= 256 \\ \sqrt{x^2 + y^2 + z^2} &= 16. \end{align*}$ Since point $A = (0,0,0), PA = 16$ , and since we scaled the answer is $16 \cdot 12 = \boxed{192}$ .

~Aaryabhatta1

Solution 3

Let $E$ be the vertex of the cube such that $ABED$ is a square. Using the British Flag Theorem, we can easily show that $PA^2 + PE^2 = PB^2 + PD^2$ and $PA^2 + PG^2 = PC^2 + PE^2$ Hence, by adding the two equations together, we get $2PA^2 + PG^2 = PB^2 + PC^2 + PD^2$ . Substituting in the values we know, we get $2PA^2 + 7\cdot 36^2 =10\cdot60^2 + 5\cdot 60^2 + 2\cdot 120^2$ .

Thus, we can solve for $PA$ , which ends up being $\boxed{192}$ .

(Lokman GÖKÇE)

Solution 4

For all points $X$ in space, define the function $f:\mathbb{R}^{3}\rightarrow\mathbb{R}$ by $f(X)=PX^{2}-GX^{2}$ . Then $f$ is linear; let $O=\frac{2A+G}{3}$ be the center of $\triangle BCD$ . Then since $f$ is linear, $\begin{align*} 3f(O)=f(B)+f(C)+f(D)&=2f(A)+f(G) \\ \left(PB^{2}-GB^{2}\right)+\left(PC^{2}-GC^{2}\right)+\left(PD^{2}-GD^{2}\right)&=2\left(PA^{2}-GA^{2}\right)+PG^{2} \\ \left(60\sqrt{10}\right)^{2}-2x^{2}+\left(60\sqrt{5}\right)^{2}-2x^{2}+\left(120\sqrt{2}\right)^{2}-2x^{2}&=2PA^{2}-2\cdot 3x^{2}+\left(36\sqrt{7}\right)^{2}, \end{align*}$ where $x$ denotes the side length of the cube. Thus $\begin{align*} 36\text{,}000+18\text{,}000+28\text{,}800-6x^{2}&=2PA^{2}-6x^{2}+9072 \\ 82\text{,}800-6x^{2}&=2PA^{2}-6x^{2}+9072 \\ 73\text{,}728&=2PA^{2} \\ 36\text{,}864&=PA^{2} \\ PA&=\boxed{192}. \end{align*}$

@@ Line 63: / Line 63: @@
 \end{align*}</cmath>
-==Video Solution by Punxsutawney Phil==
-https://youtube.com/watch?v=vaRfI0l4s_8
 ==See Also==

2021 AIME I (Problems • Answer Key • Resources)
Preceded by Problem 5	Followed by Problem 7
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search