Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "User:Afly"

(→‎Rotating cube)
m (→‎Function f(x) = 3\tanh (x)+\sin (x))
 
(47 intermediate revisions by 2 users not shown)
Line 1: Line 1:
 +
=Afly's notes=
 +
 
==About Afly==
 
==About Afly==
  
Line 4: Line 6:
  
 
User # 1013218 [https://artofproblemsolving.com/community/user/1013218 Profile]
 
User # 1013218 [https://artofproblemsolving.com/community/user/1013218 Profile]
 +
 +
Competitions I have participated in:
 +
 +
AMC8 * 2
 +
 +
AMC10A * 1
 +
 +
AMC10B * 1
 +
 +
MathLeague Qualifications * 7
 +
 +
MathLeague District * 1
 +
 +
MathLeague District Countdown * 1
 +
 +
MathLeague State * 1
 +
 +
MathLeague State Countdown * 1
 +
 +
MathLeague National * 2
 +
 +
MathLeague National Countdown * 1
 +
 +
MathLeague International * 2
 +
 +
Favorite pythagorean triples:
 +
 +
3-4-5
 +
5-12-13
 +
7-24-25
 +
9-40-41
 +
11-60-61
 +
13-84-85
 +
 +
8-15-17
 +
12-35-37
 +
16-63-65
 +
20-99-101
 +
 +
20-21-29
 +
28-45-53
 +
36-77-85
 +
44-117-125
 +
 +
48-55-73
 +
96-247-265
 +
 +
88-105-137
 +
(Those last three are collector's edition)
 +
 +
60-91-109 (Fun one!)
 +
 +
84-187-205 (Weird)
 +
 +
65-72-97 (Even stranger)
 +
 +
33-56-65 (WHAAT?)
 +
 +
==Visual proofs==
 +
(Demonstrates HI IQ)
 +
===FAQ: What is a triangular number?===
 +
n=3
 +
┌─┐ 1
 +
├─┴─┐ 2
 +
├───┴─┐ 3
 +
└─────┘
 +
2 of them are:
 +
┌─┐      ┌─┐   
 +
├─┴─┐    ├─┴─┐ 
 +
├───┴─┐  ├───┴─┐
 +
└─────┘  └─────┘
 +
Which are:
 +
┌─┐      ┌─────┐   
 +
├─┴─┐    └─┬───┤ 
 +
├───┴─┐    └─┬─┤
 +
└─────┘      └─┘
 +
 +
And...
 +
 +
┌─┬─────┐
 +
├─┴─┬───┤ n
 +
├───┴─┬─┤
 +
└─────┴─┘
 +
    n+1
 +
so 2(1+2+3...+n)=n(n+1)
 +
 +
They're special characters in unicode. deal with it.
 +
 +
It was a pain to make. I should have used my Maze class in python.
  
 
==Some of my asymptote creations==
 
==Some of my asymptote creations==
Line 9: Line 100:
 
These are a random collection of diagrams and text that I have made. YOU ARE ALLOWED TO USE THESE IMAGES AND/OR TEXT IN YOUR PAGES OR USE THEM FOR REFERENCE.
 
These are a random collection of diagrams and text that I have made. YOU ARE ALLOWED TO USE THESE IMAGES AND/OR TEXT IN YOUR PAGES OR USE THEM FOR REFERENCE.
  
−
I try to put them in the order of how much technique &  technical points there are in them  
+
I try to put them in the order of how much technique &  technical points there are in them
 +
 
 +
Enough talking. Let's get into the pictures.
  
 
===Triangle===
 
===Triangle===
 +
 +
Starring: Basic path drawing and LaTeX
  
 
<asy>
 
<asy>
Line 67: Line 162:
  
 
===Pythagorean===
 
===Pythagorean===
 +
 +
Starring: Colored paths and line width
  
 
<asy>
 
<asy>
Line 90: Line 187:
 
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
 
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
  
−
===Isosceles Trapezoid===
+
===Trapezoid===
 +
 
 +
Starring: Filling regions
  
 
<asy>
 
<asy>
Line 121: Line 220:
  
 
===Hexagon (In AMC 2023 10A #24)===
 
===Hexagon (In AMC 2023 10A #24)===
 +
 +
Starring: polygon(), shift(), dir(), unitsize, labels
  
 
<asy>
 
<asy>
Line 158: Line 259:
  
 
====Grid with numbers====
 
====Grid with numbers====
 +
 +
Starring: Custom colors
  
 
<asy>
 
<asy>
Line 206: Line 309:
  
 
===Tiny 3D experiments===
 
===Tiny 3D experiments===
 +
 +
Starring: Using cleverly placed colors and lines to make a illusion (just pure skill, not really Asymptote)
  
 
====Cube====
 
====Cube====
Line 265: Line 370:
 
</asy>
 
</asy>
  
 +
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
 +
===Pascal's triangle mod===
 +
Starring: Loops and arrays
 +
====mod 2====
 +
<asy>
 +
int[][] pascal={{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{}};
 +
pen p1=rgb(1/8,1/8,7/8);
 +
pen p2=rgb(1/8,7/8,1/8);
 +
for (int i=0; i<64; ++i)
 +
{
 +
for (int j=0; j<i+1; ++j)
 +
{
 +
  if (j==0 || i==j) {
 +
  pascal[i].push(1);
 +
  } else {
 +
  pascal[i].push(pascal[i-1][j-1]+pascal[i-1][j]);
 +
  }
 +
  if (pascal[i][j]%2==0){
 +
  fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p1);
 +
  } else {
 +
  fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p2);
 +
  }
 +
}
 +
}
 +
</asy>
 +
====mod 2 big====
 +
<asy>
 +
int[][] pascal1={{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{}};
 +
pen p1=rgb(1/8,1/8,7/8);
 +
pen p2=rgb(1/8,7/8,1/8);
 +
for (int i=0; i<64; ++i)
 +
{
 +
for (int j=0; j<i+1; ++j)
 +
{
 +
  if (j==0 || i==j) {
 +
  pascal1[i].push(1);
 +
  } else {
 +
  pascal1[i].push(pascal1[i-1][j-1]+pascal1[i-1][j]);
 +
  }
 +
  if (pascal1[i][j]%2==0){
 +
  fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p1);
 +
  } else {
 +
  fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p2);
 +
  }
 +
}
 +
}
 +
int[] ref1=pascal1[63];
 +
int[][] pascal2={{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{}};
 +
pen p1=rgb(1/8,1/8,7/8);
 +
pen p2=rgb(1/8,7/8,1/8);
 +
for (int i=0; i<64; ++i)
 +
{
 +
for (int j=0; j<i+65; ++j)
 +
{
 +
  if (j==0 || i==j) {
 +
  pascal2[i].push(1);
 +
  } else {
 +
  if (i==0){
 +
    pascal2[i].push(ref[j-1]+ref[j]);
 +
  } else {
 +
    pascal2[i].push(pascal2[i-1][j-1]+pascal2[i-1][j]);
 +
  }
 +
  }
 +
  if (pascal1[i][j]%2==0){
 +
  fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*(i+64)*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p1);
 +
  } else {
 +
  fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*(i+64)*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p2);
 +
  }
 +
}
 +
}
 +
</asy>
 +
====mod 3====
 +
<asy>
 +
int[][] pascal={{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{}};
 +
pen p1=rgb(1/8,1/8,7/8);
 +
pen p2=rgb(1/8,7/8,1/8);
 +
pen p3=rgb(7/8,1/8,1/8);
 +
for (int i=0; i<64; ++i)
 +
{
 +
for (int j=0; j<i+1; ++j)
 +
{
 +
  if (j==0 || i==j) {
 +
  pascal[i].push(1);
 +
  } else {
 +
  pascal[i].push(pascal[i-1][j-1]+pascal[i-1][j]);
 +
  }
 +
  if (pascal[i][j]%3==0){
 +
  fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p1);
 +
  } else {
 +
  if (pascal[i][j]%3==1) {
 +
    fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p2);
 +
  } else {
 +
    fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p3);
 +
  }
 +
  }
 +
}
 +
}
 +
</asy>
 +
====mod 4====
 +
<asy>
 +
int[][] pascal={{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{}};
 +
pen p1=rgb(1/8,1/8,7/8);
 +
pen p2=rgb(1/8,7/8,1/8);
 +
pen p3=rgb(7/8,1/8,1/8);
 +
pen p4=rgb(7/8,7/8,1/8);
 +
for (int i=0; i<64; ++i)
 +
{
 +
for (int j=0; j<i+1; ++j)
 +
{
 +
  if (j==0 || i==j) {
 +
  pascal[i].push(1);
 +
  } else {
 +
  pascal[i].push(pascal[i-1][j-1]+pascal[i-1][j]);
 +
  }
 +
  if (pascal[i][j]%4==0){
 +
  fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p1);
 +
  } else {
 +
  if (pascal[i][j]%4==1) {
 +
    fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p2);
 +
  } else {
 +
    if (pascal[i][j]%4==2) {
 +
    fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p3);
 +
    } else {
 +
    fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p4);
 +
    }
 +
  }
 +
  }
 +
}
 +
}
 +
</asy>
 +
====mod 5====
 +
<asy>
 +
int[][] pascal={{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{}};
 +
pen p1=rgb(1/8,1/8,7/8);
 +
pen p2=rgb(1/8,7/8,1/8);
 +
pen p3=rgb(7/8,1/8,1/8);
 +
pen p4=rgb(7/8,7/8,1/8);
 +
pen p5=rgb(1/8,7/8,7/8);
 +
for (int i=0; i<64; ++i)
 +
{
 +
for (int j=0; j<i+1; ++j)
 +
{
 +
  if (j==0 || i==j) {
 +
  pascal[i].push(1);
 +
  } else {
 +
  pascal[i].push(pascal[i-1][j-1]+pascal[i-1][j]);
 +
  }
 +
  if (pascal[i][j]%5==0){
 +
  fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p1);
 +
  } else {
 +
  if (pascal[i][j]%5==1) {
 +
    fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p2);
 +
  } else {
 +
    if (pascal[i][j]%5==2) {
 +
    fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p3);
 +
    } else {
 +
    if (pascal[i][j]%5==3) {
 +
      fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p4);
 +
    } else {
 +
      fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p5);
 +
    }
 +
    }
 +
  }
 +
  }
 +
}
 +
}
 +
</asy>
 +
====mod 6====
 +
<asy>
 +
int[][] pascal={{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{}};
 +
pen p1=rgb(1/8,1/8,7/8);
 +
pen p2=rgb(1/8,7/8,1/8);
 +
pen p3=rgb(7/8,1/8,1/8);
 +
pen p4=rgb(7/8,7/8,1/8);
 +
pen p5=rgb(1/8,7/8,7/8);
 +
pen p6=rgb(7/8,1/8,7/8);
 +
for (int i=0; i<64; ++i)
 +
{
 +
for (int j=0; j<i+1; ++j)
 +
{
 +
  if (j==0 || i==j) {
 +
  pascal[i].push(1);
 +
  } else {
 +
  pascal[i].push(pascal[i-1][j-1]+pascal[i-1][j]);
 +
  }
 +
  if (pascal[i][j]%6==0){
 +
  fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p1);
 +
  } else {
 +
  if (pascal[i][j]%6==1) {
 +
    fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p2);
 +
  } else {
 +
    if (pascal[i][j]%6==2) {
 +
    fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p3);
 +
    } else {
 +
    if (pascal[i][j]%6==3) {
 +
      fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p4);
 +
    } else {
 +
      if (pascal[i][j]%6==4) {
 +
      fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p5);
 +
      } else {
 +
      fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p6);
 +
      }
 +
    }
 +
    }
 +
  }
 +
  }
 +
}
 +
}
 +
</asy>
 +
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
 +
 +
===How trig works===
 +
Latex + Asymptote
 +
<asy>
 +
import olympiad;
 +
markscalefactor = 1/96;
 +
real d = radians(40);
 +
unitsize(72);
 +
pair O = (0,0);
 +
draw(circle(O,1));
 +
dot(O);
 +
label("O",O,dir(180+degrees(d)/2));
 +
label("$\theta$",shift(dir(degrees(d)/2)/5)*O,dir(degrees(d)/2));
 +
pair G = (0,1);
 +
label("G",G,N);
 +
pair A = (cos(d),0);
 +
label("A",A,S);
 +
pair B = (cos(d),sin(d));
 +
label("B",B,dir(135+degrees(d)));
 +
pair C = (1,0);
 +
label("C",C,E);
 +
pair D = (1,tan(d));
 +
label("D",D,N);
 +
pair E = (1/tan(d),0);
 +
label("E",E,SE);
 +
pair F = (1/tan(d),1);
 +
label("F",F,N);
 +
pair G = (0,1);
 +
label("G",G,N);
 +
draw(D--O--C--D--B--A--E--F--G--O--F);
 +
draw(rightanglemark(G,O,C));
 +
label("$\cos \theta$",O--A);
 +
label("$\sin \theta$",B--A);
 +
label("1",B--O);
 +
draw(shift(dir(270)/24)*brace(C,O));
 +
label("$\cot \theta$",shift(dir(270)/24)*brace(C,O),S);
 +
draw(shift(dir(d+90)/24)*brace(O,D));
 +
label("$\csc \theta$",shift(dir(degrees(d)+90)/24)*brace(O,D),dir(degrees(d)+90));
 +
draw(shift(dir(270)/4)*brace(E,O));
 +
label("1",shift(dir(270)/4)*brace(C,O),S);
 +
draw(shift(dir(270)/4)*O--shift(dir(270)/24)*O);
 +
draw(shift(dir(270)/4)*E--shift(dir(270)/24)*E);
 +
label("1",E--F,SW);
 +
label("$\tan \theta$",D--E);
 +
draw(shift(dir(degrees(d)+90)/4)*brace(O,F));
 +
label("$\sec \theta$",shift(dir(degrees(d)+90)/4)*brace(O,F),dir(d+90));
 +
draw(shift(dir(degrees(d)+90)/4)*O--shift(dir(degrees(d)+90)/24)*O);
 +
draw(shift(dir(degrees(d)+90)/4)*F--shift(dir(degrees(d)+90)/24)*F);
 +
</asy>
 +
 +
<math>\textit{\textbf{\underline{\fontsize{24}{36}\selectfont Identities}}}</math>
 +
 +
<math>\textit{\textbf{\underline{\fontsize{18}{27}\selectfont Pythagorean identities}}}</math>
 +
 +
<math>\text{\fontsize{12}{18}\selectfont We see three right triangles in the diagrams which we can get identities out of: }</math>
 +
 +
<math>\fontsize{12}{18}\selectfont \triangle OAB \text{ gives } \sin^2 \theta + \cos^2 \theta = 1^2</math>
 +
 +
<math>\fontsize{12}{18}\selectfont \triangle OCD \text{ gives } \tan^2 \theta + 1^2 = \sec^2 \theta</math>
 +
 +
<math>\fontsize{12}{18}\selectfont \triangle OEF \text{ gives } 1^2 + \cot^2 \theta = \csc^2 \theta</math>
 +
 +
<math>\textit{\textbf{\underline{\fontsize{18}{27}\selectfont Similarity identities}}}</math>
 +
 +
<math>\text{\fontsize{12}{18}\selectfont We can also get identities out of similar triangles: }</math>
 +
 +
<math>\fontsize{15}{22.5}\selectfont \triangle OAB \sim \triangle OCD\text{ gives:}</math>
 +
 +
<math>\fontsize{12}{18}\selectfont \frac{1}{\cos \theta} = \frac{\sec \theta}{1}</math>
 +
 +
<math>\fontsize{12}{18}\selectfont \frac{1}{\sin \theta} = \frac{\sec \theta}{\tan \theta}</math>
 +
 +
<math>\fontsize{12}{18}\selectfont \frac{\cos \theta}{1} = \frac{1}{\sec \theta}</math>
 +
 +
<math>\fontsize{12}{18}\selectfont \frac{\cos \theta}{\sin \theta} = \frac{1}{\tan \theta}</math>
 +
 +
<math>\fontsize{12}{18}\selectfont \frac{\sin \theta}{1} = \frac{\tan \theta}{\sec \theta}</math>
 +
 +
<math>\fontsize{12}{18}\selectfont \frac{\sin \theta}{\cos \theta} = \frac{\tan \theta}{1}</math>
 +
 +
<math>\fontsize{15}{22.5}\selectfont \triangle OAB \sim \triangle OEF\text{ gives:}</math>
 +
 +
<math>\fontsize{12}{18}\selectfont \frac{1}{\cos \theta} = \frac{\csc \theta}{\cot \theta}</math>
 +
 +
<math>\fontsize{12}{18}\selectfont \frac{1}{\sin \theta} = \frac{\csc \theta}{1}</math>
 +
 +
<math>\fontsize{12}{18}\selectfont \frac{\cos \theta}{1} = \frac{\cot \theta}{\csc \theta}</math>
 +
 +
<math>\fontsize{12}{18}\selectfont \frac{\cos \theta}{\sin \theta} = \frac{\cot \theta}{1}</math>
 +
 +
<math>\fontsize{12}{18}\selectfont \frac{\sin \theta}{1} = \frac{1}{\csc \theta}</math>
 +
 +
<math>\fontsize{12}{18}\selectfont \frac{\sin \theta}{\cos \theta} = \frac{1}{\cot \theta}</math>
 +
 +
<math>\fontsize{15}{22.5}\selectfont \triangle OCD \sim \triangle OEF\text{ gives:}</math>
 +
 +
<math>\fontsize{12}{18}\selectfont \frac{\sec \theta}{1} = \frac{\csc \theta}{\cot \theta}</math>
 +
 +
<math>\fontsize{12}{18}\selectfont \frac{\sec \theta}{\tan \theta} = \frac{\csc \theta}{1}</math>
 +
 +
<math>\fontsize{12}{18}\selectfont \frac{1}{\sec \theta} = \frac{\cot \theta}{\csc \theta}</math>
 +
 +
<math>\fontsize{12}{18}\selectfont \frac{1}{\tan \theta} = \frac{\cot \theta}{1}</math>
 +
 +
<math>\fontsize{12}{18}\selectfont \frac{\tan \theta}{\sec \theta} = \frac{1}{\csc \theta}</math>
 +
 +
<math>\fontsize{12}{18}\selectfont \frac{\tan \theta}{1} = \frac{1}{\cot \theta}</math>
 
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
 
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
  
−
====Rotating cube====
+
===Rotating cube===
  
−
=====Perspective=====
+
Starring: Asymptote three
 +
 
 +
====Perspective====
  
 
<asy>
 
<asy>
Line 343: Line 767:
 
</asy>
 
</asy>
  
−
=====Orthographic=====
+
====Orthographic====
  
 
<asy>
 
<asy>
Line 416: Line 840:
 
draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle,red);
 
draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle,red);
 
</asy>
 
</asy>
 +
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
  
 
===Circle diagrams===
 
===Circle diagrams===
Line 422: Line 847:
  
 
====Intersection points====
 
====Intersection points====
 +
 +
Starring: Fancy labels, Troubleshooting
  
 
<asy>
 
<asy>
Line 518: Line 945:
 
label("$I_{3b}$",C3,dir(0),blue);
 
label("$I_{3b}$",C3,dir(0),blue);
 
</asy>
 
</asy>
 +
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
 +
===Function <math>f(x) = 3\tanh (x)+\sin (x)</math>===
 +
Starring: Functions
 +
<asy>
 +
unitsize(8);
 +
pair f(real x1){
 +
real y1 = 3*tanh(x1)+(sin(x1));
 +
pair p1 = (x1,y1);
 +
return p1;
 +
}
 +
pair[] plotpoints = {};
 +
for (int i=0;i<2001;++i){
 +
plotpoints.push(f((i/100)-10));
 +
}
 +
for (int i=0;i<2000;++i){
 +
draw(plotpoints[i]--plotpoints[i+1],linewidth(0.5)+blue);
 +
}
 +
</asy>
 +
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
 +
 +
===Sheet===
 +
Starring: Bezier surfaces
 +
<asy>
 +
import three;
 +
currentprojection=orthographic(1,1,5);
 +
size(200);
 +
pair[] l1x={(-2,0), (-1.3,0.5), (-0.7,0.5), (0,0)};
 +
pair[] l1y={(-2,0), (-1.3,0.5), (-0.7,0.5), (0,0)};
 +
triple f1(int xp, int yp)
 +
{
 +
real Z = l1x[xp].y + l1y[yp].y;
 +
real X = l1x[xp].x;
 +
real Y = l1y[yp].x;
 +
triple pt = (X,Y,Z);
 +
return pt;
 +
};
 +
triple[][] P1={{},{},{},{}};
 +
for (int i=0;i<4;++i){
 +
for (int j=0; j<4;++j){
 +
  triple[] temp = P1[i];
 +
  temp.push(f1(i,j));
 +
  P1.delete(i);
 +
  P1.insert(i,temp);
 +
}
 +
}
 +
for (int i=0;i<4;++i){
 +
for (int j=0; j<4;++j){
 +
  dot(P1[i][j]);
 +
}
 +
}
 +
draw(surface(patch(P1,new pen[]{cyan,cyan+green,cyan+yellow+green+red,cyan+yellow})));
 +
pair[] l2x={(-2,0), (-1.3,0.5), (-0.7,0.5), (0,0)};
 +
pair[] l2y={(0,0), (0.7,-0.5), (1.3,-0.5), (2,0)};
 +
triple f2(int xp, int yp)
 +
{
 +
real Z = l2x[xp].y + l2y[yp].y;
 +
real X = l2x[xp].x;
 +
real Y = l2y[yp].x;
 +
triple pt = (X,Y,Z);
 +
return pt;
 +
};
 +
triple[][] P2={{},{},{},{}};
 +
for (int i=0;i<4;++i){
 +
for (int j=0; j<4;++j){
 +
  triple[] temp = P2[i];
 +
  temp.push(f2(i,j));
 +
  P1.delete(i);
 +
  P1.insert(i,temp);
 +
}
 +
}
 +
for (int i=0;i<4;++i){
 +
for (int j=0; j<4;++j){
 +
  dot(P2[i][j]);
 +
}
 +
}
 +
draw(surface(patch(P2,new pen[]{cyan+yellow,cyan+yellow+green+red,yellow+red,yellow})));
 +
pair[] l3x={(0,0), (0.7,-0.5), (1.3,-0.5), (2,0)};
 +
pair[] l3y={(-2,0), (-1.3,0.5), (-0.7,0.5), (0,0)};
 +
triple f3(int xp, int yp)
 +
{
 +
real Z = l3x[xp].y + l3y[yp].y;
 +
real X = l3x[xp].x;
 +
real Y = l3y[yp].x;
 +
triple pt = (X,Y,Z);
 +
return pt;
 +
};
 +
triple[][] P3={{},{},{},{}};
 +
for (int i=0;i<4;++i){
 +
for (int j=0; j<4;++j){
 +
  triple[] temp = P3[i];
 +
  temp.push(f3(i,j));
 +
  P3.delete(i);
 +
  P3.insert(i,temp);
 +
}
 +
}
 +
for (int i=0;i<4;++i){
 +
for (int j=0; j<4;++j){
 +
  dot(P3[i][j]);
 +
}
 +
}
 +
draw(surface(patch(P3,new pen[]{cyan+green,green,green+red,cyan+yellow+green+red})));
 +
pair[] l4x={(0,0), (0.7,-0.5), (1.3,-0.5), (2,0)};
 +
pair[] l4y={(0,0), (0.7,-0.5), (1.3,-0.5), (2,0)};
 +
triple f4(int xp, int yp)
 +
{
 +
real Z = l4x[xp].y + l4y[yp].y;
 +
real X = l4x[xp].x;
 +
real Y = l4y[yp].x;
 +
triple pt = (X,Y,Z);
 +
return pt;
 +
};
 +
triple[][] P4={{},{},{},{}};
 +
for (int i=0;i<4;++i){
 +
for (int j=0; j<4;++j){
 +
  triple[] temp = P4[i];
 +
  temp.push(f4(i,j));
 +
  P4.delete(i);
 +
  P4.insert(i,temp);
 +
}
 +
}
 +
for (int i=0;i<4;++i){
 +
for (int j=0; j<4;++j){
 +
  dot(P4[i][j]);
 +
}
 +
}
 +
draw(surface(patch(P4,new pen[]{cyan+yellow+green+red,green+red,red,yellow+red})));
 +
import settings;
 +
leftbutton=new string[] {"rotate","zoom","shift","pan"};
 +
middlebutton=new string[] {"menu"};
 +
rightbutton=new string[] {"zoom/menu","rotateX","rotateY","rotateZ"};
 +
wheelup=new string[] {"zoomin"};
 +
wheeldown=new string[] {"zoomout"};
 +
</asy>
 +
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
 +
===Another cube===
 +
Starring: Knowledge*
 +
<asy>
 +
unitsize(72);
 +
pen drawing = red;
 +
// change it!
 +
real rxy = acos(1/1.5*sqrt(2));
 +
real ryz = acos(1/sqrt(3));
 +
real[] unitx = {cos(rxy),-sin(rxy)*cos(ryz),sin(rxy)*sin(ryz)};
 +
real[] unity = {sin(rxy),cos(rxy)*cos(ryz),-cos(rxy)*sin(ryz)};
 +
real[] unitz = {0,sin(ryz),cos(ryz)};
 +
real[][] base = {unitx,unity,unitz};
 +
pair proj(real[] coor){
 +
pair ortho(real[] coor){
 +
  pair p=(coor[0],coor[1]);
 +
  return p;
 +
}
 +
pair perspec(real[] coor){
 +
  real[] center = {0,0,0};
 +
  // Write the projection center above
 +
  real d = (coor[0]-center[0])**2+(coor[1]-center[1])**2+(coor[2]-center[2])**2;
 +
  pair p=(coor[0]/d,coor[1]/d);
 +
  return p;
 +
}
 +
pair p = ortho(coor);
 +
// Choose your projection above
 +
return p;
 +
}
 +
real[] newp(real[] s,real[][] base){
 +
real[] ad(real[] in1,real[] in2,real[] in3){
 +
  real[] out = {in1[0]+in2[0]+in3[0],in1[1]+in2[1]+in3[1],in1[2]+in2[2]+in3[2]};
 +
  return out;
 +
}
 +
real[] mul(real fac,real[] in){
 +
  real[] out = {fac*in[0],fac*in[1],fac*in[2]};
 +
  return out;
 +
}
 +
real[] out = ad(mul(s[0],base[0]),mul(s[1],base[1]),mul(s[2],base[2]));
 +
return out;
 +
}
 +
for (real i=0;i<2;++i){
 +
for (real j=0;j<2;++j){
 +
  for (real k=0;k<2;++k){
 +
  real[] Orig = {i,j,k};
 +
  real[] Ivar = {1-i,j,k};
 +
  real[] Jvar = {i,1-j,k};
 +
  real[] Kvar = {i,j,1-k};
 +
  pair orig = proj(newp(Orig,base));
 +
  pair ivar = proj(newp(Ivar,base));
 +
  pair jvar = proj(newp(Jvar,base));
 +
  pair kvar = proj(newp(Kvar,base));
 +
  draw(orig--ivar,drawing);
 +
  draw(orig--jvar,drawing);
 +
  draw(orig--kvar,drawing);
 +
  }
 +
}
 +
}
 +
</asy>
 +
* How to put everything together in a nice example, why the only good thing about asymptote three is bezier surfaces. If you're bored, look at the code and try to figure out how it all works.
  
 
==Created files==
 
==Created files==
Line 582: Line 1,202:
  
  
 +
[https://artofproblemsolving.com/wiki/index.php/File:Colored_dodecagon.png File]
  
−
5/6 size: [[File:Colored dodecagon.png|700px|thumb]]
+
===Pentagon 2023 12B Q25 dissmo===
  
 +
Original size: [[File:Pentagon 2023 12B Q25 dissmo.png|820px|thumb]]
  
  
Line 632: Line 1,254:
  
  
 +
[https://artofproblemsolving.com/wiki/index.php/File:Pentagon_2023_12B_Q25_dissmo.png File]
  
−
2/3 size: [[File:Colored dodecagon.png|560px|thumb]]
+
==LaTeX Creations (coming soon!)==
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
1/2 size: [[File:Colored dodecagon.png|420px|thumb]]
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
1/3 size: [[File:Colored dodecagon.png|280px|thumb]]
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
1/6 size: [[File:Colored dodecagon.png|140px|thumb]]
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
===Pentagon 2023 12B Q25 dissmo===
 
−
 
 
−
Original size: [[File:Pentagon 2023 12B Q25 dissmo.png|820px|thumb]]
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
  
 +
==Created pages==
 +
*[[Proofs of trig identities]]
  
 +
==Solutions created==
  
 +
===2019 AIME II #4 Solution 7 (Generating functions)===
 +
[[https://artofproblemsolving.com/wiki/index.php/2019_AIME_II_Problems/Problem_4#Solution_7.28Generating_functions.29 Actual solution]]
  
 +
Let's look at the prime factorization of some of these rolls:
  
 +
  01 => 2^0*3^0*5^0
 +
  02 => 2^1*3^0*5^0
 +
  03 => 2^0*3^1*5^0
 +
  04 => 2^2*3^0*5^0
 +
  05 => 2^0*3^0*5^1
 +
  06 => 2^1*3^1*5^0
  
 +
Now, using multi-variable generating functions, we get:
  
 +
  f(x,y,z)=1+x+y+x^2+z+xy
 +
            | |
 +
            \| |/
 +
            'v'
 +
  f(x,y,z)=1+x+y+z+x^2+xy
 +
    =(for our purposes)
 +
        =2+x+y+z+xy
  
 +
Let's square that!
  
 +
  4+2x+2y+2z+2xy+2x+x^2+xy+xz+x^2y+2y+xy+y^2+yz+xy^2+2z+xz+yz+z^2+xyz+2xy+x^2y+xy^2+xyz+x^2y^2
 +
  Combining like terms . . .
 +
  4+4x+4y+4z+x^2+y^2+z^2+6xy+2xz+2yz+2xyz+2x^2y+2xy^2+x^2y^2
  
 +
Since we only want the parity of each of the exponents, we can collapse it again.
  
 +
  8+6x+6y+4z+6xy+2xz+2yz+2xyz
  
 +
Last simplification: factor out a factor of two and save it for later.
  
 +
  4+3x+3y+2z+3xy+xz+yz+xyz
  
 +
Let's take a better approach this time.
  
 +
  ___ term :4*4+3*3+3*3+2*2+3*3+1*1+1*1+1*1=16+09+09+04+09+01+01+01=50
 +
  __x term :4*3+3*4+3*3+2*1+3*3+1*2+1*1+1*1=12+12+09+02+09+02+01+01=48
 +
  __y term :4*3+3*3+3*4+2*1+3*3+1*1+1*2+1*1=12+09+12+02+09+01+02+01=48
 +
  __z term :4*2+3*1+3*1+2*4+3*1+1*3+1*3+1*3=08+03+03+08+03+03+03+03=34
 +
  _xy term :4*3+3*3+3*3+2*1+3*4+1*1+1*1+1*2=12+09+09+02+12+01+01+02=48
 +
  _xz term :4*1+3*2+3*1+2*3+3*1+1*4+1*3+1*3=04+06+03+06+03+04+03+03=32
 +
  _yz term :4*1+3*1+3*2+2*3+3*1+1*3+1*4+1*3=04+03+06+06+03+03+04+03=32
 +
  xyz term :4*1+3*1+3*1+2*3+3*2+1*3+1*3+1+4=04+03+03+06+06+03+03+04=32
 +
 
 +
  Result: 50+48x+48y+34z+48xy+32xz+32yz+32xyz
  
 +
I know we could use vectors and dot products to make it look neater but ''come on''. It '''already''' looks neat enough.
 +
Also, we didn't ''need'' the other parts, but it just ''looks '''nicer'''''.
 +
Now let's stick back the two that turned into a four.
  
 +
  200+192x+192y+136z+192xy+128xz+128yz+128xyz
  
 +
We seek the constant term which is 200. 200/1296=100/648=50/324=25/162, 25+162=187
  
 +
=Yrock's Notes=
  
 +
hello
  
 +
=ConfidentFlamingo's notes=
  
 +
=Other Users' notes=
  
−
4/5 size: [[File:Pentagon 2023 12B Q25 dissmo.png|656px|thumb]]
+
Note from afly: If you leave a note, write who it is from

Latest revision as of 16:26, 20 October 2024

Afly's notes

About Afly

Friends with Yrock and ConfidentFlamingo

User # 1013218 Profile

Competitions I have participated in:

AMC8 * 2

AMC10A * 1

AMC10B * 1

MathLeague Qualifications * 7

MathLeague District * 1

MathLeague District Countdown * 1

MathLeague State * 1

MathLeague State Countdown * 1

MathLeague National * 2

MathLeague National Countdown * 1

MathLeague International * 2

Favorite pythagorean triples: 

3-4-5
5-12-13
7-24-25
9-40-41
11-60-61
13-84-85

8-15-17
12-35-37
16-63-65
20-99-101

20-21-29
28-45-53
36-77-85
44-117-125

48-55-73
96-247-265

88-105-137
(Those last three are collector's edition)

60-91-109 (Fun one!)

84-187-205 (Weird)

65-72-97 (Even stranger)

33-56-65 (WHAAT?)

Visual proofs

(Demonstrates HI IQ)

FAQ: What is a triangular number?

n=3 

┌─┐ 1
├─┴─┐ 2
├───┴─┐ 3
└─────┘

2 of them are: 

┌─┐      ┌─┐     
├─┴─┐    ├─┴─┐   
├───┴─┐  ├───┴─┐ 
└─────┘  └─────┘

Which are: 

┌─┐      ┌─────┐     
├─┴─┐    └─┬───┤  
├───┴─┐    └─┬─┤ 
└─────┘      └─┘

And... 

┌─┬─────┐
├─┴─┬───┤ n
├───┴─┬─┤
└─────┴─┘
   n+1

so 2(1+2+3...+n)=n(n+1)

They're special characters in unicode. deal with it.

It was a pain to make. I should have used my Maze class in python.

Some of my asymptote creations

These are a random collection of diagrams and text that I have made. YOU ARE ALLOWED TO USE THESE IMAGES AND/OR TEXT IN YOUR PAGES OR USE THEM FOR REFERENCE.

I try to put them in the order of how much technique & technical points there are in them

Enough talking. Let's get into the pictures.

Triangle

Starring: Basic path drawing and LaTeX

[asy] pair A=(0,0); pair B=(2,0); pair C=(1,sqrt(3)); draw(A--B--C); draw(A--C--B); [/asy]

$\text{That is a equilateral triangle with side length 2!}$

$\text{The height is } \sqrt{2^2-1^2} = \sqrt{3}$

$\text{The area is } 2 \cdot \sqrt{3} \cdot \frac{1}{2} = \boxed{\sqrt{3}}$

$\dots$

[asy] pair A=(0,0); pair B=(0,2); pair C=(1,1); draw(A--B--C); draw(A--C--B); [/asy]

$\text{Homework: calculate the area}$

ANSWER: LOOK ONLY WHEN THE PROBLEM IS COMPLETED >>> THIS IS ONLY TO CHECK YOUR ANSWER

$\text{This is an isosceles right triangle. It has side length }\sqrt{2}$

$\text{It has an height of } \frac{\sqrt{2}}{\sqrt{2}} = 1 \text{ and a base of } \sqrt{2} \cdot \sqrt{2} = 2$

$\text{The area is } 1 \cdot 2 \cdot \frac{1}{2} = \boxed{1}$ +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

Pythagorean

Starring: Colored paths and line width

[asy] pair A=(0,0); pair B=(0,3); pair C=(4,0); draw(A--B--C--A,black+linewidth(1)); pair D=(-3,0); pair E=(-3,3); draw(A--B--E--D--A,red+linewidth(1)); pair F=(0,-4); pair G=(4,-4); draw(A--C--G--F--A,orange+linewidth(1)); pair H=(7,4); pair I=(3,7); draw(B--C--H--I--B,yellow+linewidth(1)); draw(A--B--C--A,black+linewidth(1)); [/asy] $\text{The pythagorean theorem: red plus orange equals yellow}$

+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

Trapezoid

Starring: Filling regions

[asy] pair A=(0,0); pair B=(10,0); pair C=(6,8); pair D=(2,8); pair E=(30/7,40/7); draw(A--B--C--D--A,black+linewidth(5)); fill(A--E--D--cycle,red); fill(B--E--C--cycle,yellow); dot(A); dot(B); dot(C); dot(D); dot(E); label(A,'A',SW); label(B,'B',SE); label(C,'C',NE); label(D,'D',NW); label(E,'E',S); draw(A--E--C,blue+linewidth(2)); draw(B--E--D,blue+linewidth(2)); [/asy] $\text{Given that } \overline{AB} \parallel \overline{DC} \text{ , prove that } A_\triangle AED = A_\triangle BEC .$

+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

Hexagon (In AMC 2023 10A #24)

Starring: polygon(), shift(), dir(), unitsize, labels

[asy] unitsize(5cm); draw(scale(3)*polygon(6)); filldraw(shift(dir(0)*2+dir(120)*3/7)*polygon(6), lightgray); filldraw(shift(dir(60)*2+dir(180)*3/7)*polygon(6), lightgray); filldraw(shift(dir(120)*2+dir(240)*3/7)*polygon(6), lightgray); filldraw(shift(dir(180)*2+dir(300)*3/7)*polygon(6), lightgray); filldraw(shift(dir(240)*2+dir(0)*3/7)*polygon(6), lightgray); filldraw(shift(dir(300)*2+dir(60)*3/7)*polygon(6), yellow); pair A = (0,0) + 3 * dir(300); pair B = A + 3/7 *dir(60); pair C = B + 1 * dir(180); pair D = C + 3/7 * dir(240); pair E = C + 4/7 * dir(120); pair F = E + 3/7 * dir(240); pair G = F + 4/7 * dir(240); pen p = red+linewidth(6); draw(A--B--C--D--cycle,p); draw(C--E--F--D--cycle,p); draw(F--G--D--cycle,p); label("1",(B + C)/2,dir(90)); label("1",(A + D)/2,dir(270)); label("3/7",(A + B)/2,dir(330)); label("3/7",(C + D)/2,dir(330)); label("4/7",(C+E)/2,dir(30)); label("3/7",(E+F)/2,dir(150)); label("4/7",(F+D)/2,dir(30)); label("4/7",(F+G)/2,dir(150)); label("4/7",(G+D)/2,dir(270)); [/asy]

+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

Tiny 2D experiments

Grid with numbers

Starring: Custom colors

[asy] unitsize(36); pair A1 = (0,0); pair A2 = (0,5); pair A3 = (5,5); pair A4 = (5,0); fill(A1--A2--A3--A4--cycle,gray(0.61437908496)); draw(A1--A4--A4+dir(90)--A1+dir(90)--A1+dir(90)*2--A4+dir(90)*2--A3-dir(90)*2--A2-dir(90)*2--A2-dir(90)--A3-dir(90)--A3--A2,linewidth(3)); draw(A1--A2--A2+dir(0)--A1+dir(0)--A1+dir(0)*2--A2+dir(0)*2--A3-dir(0)*2--A4-dir(0)*2--A4-dir(0)--A3-dir(0)--A3--A4,linewidth(3)); pair B1 = (0,1/2); pair B2 = (0,3/2); pair B3 = (0,5/2); pair B4 = (0,7/2); pair B5 = (0,9/2); pair C1 = (1/2,0); pair C2 = (3/2,0); pair C3 = (5/2,0); pair C4 = (7/2,0); pair C5 = (9/2,0); label("0",B1+C1); label("0",B2+C1); label("0",B3+C1); label("0",B4+C1); label("0",B5+C1); label("0",B1+C2); label("0",B2+C2); label("0",B3+C2); label("1",B4+C2); label("1",B5+C2); label("0",B1+C3); label("0",B2+C3); label("2",B3+C3); label("1",B4+C3); label("0",B5+C3); label("0",B1+C4); label("5",B2+C4); label("3",B3+C4); label("0",B4+C4); label("0",B5+C4); label("7",B1+C5); label("1",B2+C5); label("0",B3+C5); label("2",B4+C5); label("0",B5+C5); [/asy]

Tiny 3D experiments

Starring: Using cleverly placed colors and lines to make a illusion (just pure skill, not really Asymptote)

Cube

[asy] unitsize(60); pair A = (0,0); pair B = A + dir(0); pair C = A + dir(60); pair D = A + dir(120); pair E = A + dir(180); pair F = A + dir(240); pair G = A + dir(300); filldraw(A--B--C--D--cycle,orange); filldraw(A--D--E--F--cycle,blue); filldraw(A--F--G--B--cycle,gray); [/asy]

Smaller cube

[asy] unitsize(40); pair A = (0,0); pair B = A + dir(0); pair C = A + dir(60); pair D = A + dir(120); pair E = A + dir(180); pair F = A + dir(240); pair G = A + dir(300); filldraw(A--B--C--D--cycle,orange); filldraw(A--D--E--F--cycle,blue); filldraw(A--F--G--B--cycle,gray); [/asy]

Cube with a cube hole in it

[asy] unitsize(60); pair A = (0,0); pair B = A + dir(0); pair b = A + 2/3*dir(0); pair C = A + dir(60); pair c = A + 2/3*dir(60); pair D = A + dir(120); pair d = A + 2/3*dir(120); pair E = A + dir(180); pair e = A + 2/3*dir(180); pair F = A + dir(240); pair f = A + 2/3*dir(240); pair G = A + dir(300); pair g = A + 2/3*dir(300); filldraw(A--e--f--g--cycle,orange); filldraw(A--g--b--c--cycle,blue); filldraw(A--c--d--e--cycle,gray); filldraw(b--c--d--D--C--B--cycle,orange); filldraw(d--e--f--F--E--D--cycle,blue); filldraw(f--g--b--B--G--F--cycle,gray); [/asy]

+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

Pascal's triangle mod

Starring: Loops and arrays

mod 2

[asy] int[][] pascal={{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{}}; pen p1=rgb(1/8,1/8,7/8); pen p2=rgb(1/8,7/8,1/8); for (int i=0; i<64; ++i) { for (int j=0; j<i+1; ++j) { if (j==0 || i==j) { pascal[i].push(1); } else { pascal[i].push(pascal[i-1][j-1]+pascal[i-1][j]); } if (pascal[i][j]%2==0){ fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p1); } else { fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p2); } } } [/asy]

mod 2 big

int[][] pascal1={{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{}};
pen p1=rgb(1/8,1/8,7/8);
pen p2=rgb(1/8,7/8,1/8);
for (int i=0; i<64; ++i)
{
 for (int j=0; j<i+1; ++j)
 {
  if (j==0 || i==j) {
   pascal1[i].push(1);
  } else {
   pascal1[i].push(pascal1[i-1][j-1]+pascal1[i-1][j]);
  }
  if (pascal1[i][j]%2==0){
   fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p1);
  } else {
   fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p2);
  }
 }
}
int[] ref1=pascal1[63];
int[][] pascal2={{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{}};
pen p1=rgb(1/8,1/8,7/8);
pen p2=rgb(1/8,7/8,1/8);
for (int i=0; i<64; ++i)
{
 for (int j=0; j<i+65; ++j)
 {
  if (j==0 || i==j) {
   pascal2[i].push(1);
  } else {
   if (i==0){
    pascal2[i].push(ref[j-1]+ref[j]);
   } else {
    pascal2[i].push(pascal2[i-1][j-1]+pascal2[i-1][j]);
   }
  }
  if (pascal1[i][j]%2==0){
   fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*(i+64)*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p1);
  } else {
   fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*(i+64)*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p2);
  }
 }
}
 (Error making remote request. Unknown error_msg)

mod 3

[asy] int[][] pascal={{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{}}; pen p1=rgb(1/8,1/8,7/8); pen p2=rgb(1/8,7/8,1/8); pen p3=rgb(7/8,1/8,1/8); for (int i=0; i<64; ++i) { for (int j=0; j<i+1; ++j) { if (j==0 || i==j) { pascal[i].push(1); } else { pascal[i].push(pascal[i-1][j-1]+pascal[i-1][j]); } if (pascal[i][j]%3==0){ fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p1); } else { if (pascal[i][j]%3==1) { fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p2); } else { fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p3); } } } } [/asy]

mod 4

[asy] int[][] pascal={{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{}}; pen p1=rgb(1/8,1/8,7/8); pen p2=rgb(1/8,7/8,1/8); pen p3=rgb(7/8,1/8,1/8); pen p4=rgb(7/8,7/8,1/8); for (int i=0; i<64; ++i) { for (int j=0; j<i+1; ++j) { if (j==0 || i==j) { pascal[i].push(1); } else { pascal[i].push(pascal[i-1][j-1]+pascal[i-1][j]); } if (pascal[i][j]%4==0){ fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p1); } else { if (pascal[i][j]%4==1) { fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p2); } else { if (pascal[i][j]%4==2) { fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p3); } else { fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p4); } } } } } [/asy]

mod 5

[asy] int[][] pascal={{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{}}; pen p1=rgb(1/8,1/8,7/8); pen p2=rgb(1/8,7/8,1/8); pen p3=rgb(7/8,1/8,1/8); pen p4=rgb(7/8,7/8,1/8); pen p5=rgb(1/8,7/8,7/8); for (int i=0; i<64; ++i) { for (int j=0; j<i+1; ++j) { if (j==0 || i==j) { pascal[i].push(1); } else { pascal[i].push(pascal[i-1][j-1]+pascal[i-1][j]); } if (pascal[i][j]%5==0){ fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p1); } else { if (pascal[i][j]%5==1) { fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p2); } else { if (pascal[i][j]%5==2) { fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p3); } else { if (pascal[i][j]%5==3) { fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p4); } else { fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p5); } } } } } } [/asy]

mod 6

[asy] int[][] pascal={{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{},{}}; pen p1=rgb(1/8,1/8,7/8); pen p2=rgb(1/8,7/8,1/8); pen p3=rgb(7/8,1/8,1/8); pen p4=rgb(7/8,7/8,1/8); pen p5=rgb(1/8,7/8,7/8); pen p6=rgb(7/8,1/8,7/8); for (int i=0; i<64; ++i) { for (int j=0; j<i+1; ++j) { if (j==0 || i==j) { pascal[i].push(1); } else { pascal[i].push(pascal[i-1][j-1]+pascal[i-1][j]); } if (pascal[i][j]%6==0){ fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p1); } else { if (pascal[i][j]%6==1) { fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p2); } else { if (pascal[i][j]%6==2) { fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p3); } else { if (pascal[i][j]%6==3) { fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p4); } else { if (pascal[i][j]%6==4) { fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p5); } else { fill(shift(dir(60)*7)*shift(dir(30))*shift(dir(240)*i*sqrt(3))*shift(dir(0)*j*sqrt(3))*rotate(30)*polygon(6),p6); } } } } } } } [/asy] +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

How trig works

Latex + Asymptote [asy] import olympiad; markscalefactor = 1/96; real d = radians(40); unitsize(72); pair O = (0,0); draw(circle(O,1)); dot(O); label("O",O,dir(180+degrees(d)/2)); label("$\theta$",shift(dir(degrees(d)/2)/5)*O,dir(degrees(d)/2)); pair G = (0,1); label("G",G,N); pair A = (cos(d),0); label("A",A,S); pair B = (cos(d),sin(d)); label("B",B,dir(135+degrees(d))); pair C = (1,0); label("C",C,E); pair D = (1,tan(d)); label("D",D,N); pair E = (1/tan(d),0); label("E",E,SE); pair F = (1/tan(d),1); label("F",F,N); pair G = (0,1); label("G",G,N); draw(D--O--C--D--B--A--E--F--G--O--F); draw(rightanglemark(G,O,C)); label("$\cos \theta$",O--A); label("$\sin \theta$",B--A); label("1",B--O); draw(shift(dir(270)/24)*brace(C,O)); label("$\cot \theta$",shift(dir(270)/24)*brace(C,O),S); draw(shift(dir(d+90)/24)*brace(O,D)); label("$\csc \theta$",shift(dir(degrees(d)+90)/24)*brace(O,D),dir(degrees(d)+90)); draw(shift(dir(270)/4)*brace(E,O)); label("1",shift(dir(270)/4)*brace(C,O),S); draw(shift(dir(270)/4)*O--shift(dir(270)/24)*O); draw(shift(dir(270)/4)*E--shift(dir(270)/24)*E); label("1",E--F,SW); label("$\tan \theta$",D--E); draw(shift(dir(degrees(d)+90)/4)*brace(O,F)); label("$\sec \theta$",shift(dir(degrees(d)+90)/4)*brace(O,F),dir(d+90)); draw(shift(dir(degrees(d)+90)/4)*O--shift(dir(degrees(d)+90)/24)*O); draw(shift(dir(degrees(d)+90)/4)*F--shift(dir(degrees(d)+90)/24)*F); [/asy]

$\textit{\textbf{\underline{\fontsize{24}{36}\selectfont Identities}}}$

$\textit{\textbf{\underline{\fontsize{18}{27}\selectfont Pythagorean identities}}}$

$\text{\fontsize{12}{18}\selectfont We see three right triangles in the diagrams which we can get identities out of: }$

$\fontsize{12}{18}\selectfont \triangle OAB \text{ gives } \sin^2 \theta + \cos^2 \theta = 1^2$

$\fontsize{12}{18}\selectfont \triangle OCD \text{ gives } \tan^2 \theta + 1^2 = \sec^2 \theta$

$\fontsize{12}{18}\selectfont \triangle OEF \text{ gives } 1^2 + \cot^2 \theta = \csc^2 \theta$

$\textit{\textbf{\underline{\fontsize{18}{27}\selectfont Similarity identities}}}$

$\text{\fontsize{12}{18}\selectfont We can also get identities out of similar triangles: }$

$\fontsize{15}{22.5}\selectfont \triangle OAB \sim \triangle OCD\text{ gives:}$

$\fontsize{12}{18}\selectfont \frac{1}{\cos \theta} = \frac{\sec \theta}{1}$

$\fontsize{12}{18}\selectfont \frac{1}{\sin \theta} = \frac{\sec \theta}{\tan \theta}$

$\fontsize{12}{18}\selectfont \frac{\cos \theta}{1} = \frac{1}{\sec \theta}$

$\fontsize{12}{18}\selectfont \frac{\cos \theta}{\sin \theta} = \frac{1}{\tan \theta}$

$\fontsize{12}{18}\selectfont \frac{\sin \theta}{1} = \frac{\tan \theta}{\sec \theta}$

$\fontsize{12}{18}\selectfont \frac{\sin \theta}{\cos \theta} = \frac{\tan \theta}{1}$

$\fontsize{15}{22.5}\selectfont \triangle OAB \sim \triangle OEF\text{ gives:}$

$\fontsize{12}{18}\selectfont \frac{1}{\cos \theta} = \frac{\csc \theta}{\cot \theta}$

$\fontsize{12}{18}\selectfont \frac{1}{\sin \theta} = \frac{\csc \theta}{1}$

$\fontsize{12}{18}\selectfont \frac{\cos \theta}{1} = \frac{\cot \theta}{\csc \theta}$

$\fontsize{12}{18}\selectfont \frac{\cos \theta}{\sin \theta} = \frac{\cot \theta}{1}$

$\fontsize{12}{18}\selectfont \frac{\sin \theta}{1} = \frac{1}{\csc \theta}$

$\fontsize{12}{18}\selectfont \frac{\sin \theta}{\cos \theta} = \frac{1}{\cot \theta}$

$\fontsize{15}{22.5}\selectfont \triangle OCD \sim \triangle OEF\text{ gives:}$

$\fontsize{12}{18}\selectfont \frac{\sec \theta}{1} = \frac{\csc \theta}{\cot \theta}$

$\fontsize{12}{18}\selectfont \frac{\sec \theta}{\tan \theta} = \frac{\csc \theta}{1}$

$\fontsize{12}{18}\selectfont \frac{1}{\sec \theta} = \frac{\cot \theta}{\csc \theta}$

$\fontsize{12}{18}\selectfont \frac{1}{\tan \theta} = \frac{\cot \theta}{1}$

$\fontsize{12}{18}\selectfont \frac{\tan \theta}{\sec \theta} = \frac{1}{\csc \theta}$

$\fontsize{12}{18}\selectfont \frac{\tan \theta}{1} = \frac{1}{\cot \theta}$ +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

Rotating cube

Starring: Asymptote three

Perspective

[asy] import three; unitsize(3); currentprojection=perspective(2,0,1/2); draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle,red); draw((0,0,0)--(0,0,1),red); draw((0,1,0)--(0,1,1),red); draw((1,1,0)--(1,1,1),red); draw((1,0,0)--(1,0,1),red); draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle,red); [/asy]

[asy] import three; unitsize(3); currentprojection=perspective(2*Cos(15),2*Sin(15),1/2); draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle,red); draw((0,0,0)--(0,0,1),red); draw((0,1,0)--(0,1,1),red); draw((1,1,0)--(1,1,1),red); draw((1,0,0)--(1,0,1),red); draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle,red); [/asy]

[asy] import three; unitsize(3); currentprojection=perspective(2*Cos(30),2*Sin(30),1/2); draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle,red); draw((0,0,0)--(0,0,1),red); draw((0,1,0)--(0,1,1),red); draw((1,1,0)--(1,1,1),red); draw((1,0,0)--(1,0,1),red); draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle,red); [/asy]

[asy] import three; unitsize(3); currentprojection=perspective(2*Cos(45),2*Sin(45),1/2); draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle,red); draw((0,0,0)--(0,0,1),red); draw((0,1,0)--(0,1,1),red); draw((1,1,0)--(1,1,1),red); draw((1,0,0)--(1,0,1),red); draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle,red); [/asy]

[asy] import three; unitsize(3); currentprojection=perspective(2*Cos(60),2*Sin(60),1/2); draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle,red); draw((0,0,0)--(0,0,1),red); draw((0,1,0)--(0,1,1),red); draw((1,1,0)--(1,1,1),red); draw((1,0,0)--(1,0,1),red); draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle,red); [/asy]

[asy] import three; unitsize(3); currentprojection=perspective(2*Cos(75),2*Sin(75),1/2); draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle,red); draw((0,0,0)--(0,0,1),red); draw((0,1,0)--(0,1,1),red); draw((1,1,0)--(1,1,1),red); draw((1,0,0)--(1,0,1),red); draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle,red); [/asy]

Orthographic

[asy] import three; unitsize(3); currentprojection=orthographic(2,0,1/2); draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle,red); draw((0,0,0)--(0,0,1),red); draw((0,1,0)--(0,1,1),red); draw((1,1,0)--(1,1,1),red); draw((1,0,0)--(1,0,1),red); draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle,red); [/asy]

[asy] import three; unitsize(3); currentprojection=orthographic(2*Cos(15),2*Sin(15),1/2); draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle,red); draw((0,0,0)--(0,0,1),red); draw((0,1,0)--(0,1,1),red); draw((1,1,0)--(1,1,1),red); draw((1,0,0)--(1,0,1),red); draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle,red); [/asy]

[asy] import three; unitsize(3); currentprojection=orthographic(2*Cos(30),2*Sin(30),1/2); draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle,red); draw((0,0,0)--(0,0,1),red); draw((0,1,0)--(0,1,1),red); draw((1,1,0)--(1,1,1),red); draw((1,0,0)--(1,0,1),red); draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle,red); [/asy]

[asy] import three; unitsize(3); currentprojection=orthographic(2*Cos(45),2*Sin(45),1/2); draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle,red); draw((0,0,0)--(0,0,1),red); draw((0,1,0)--(0,1,1),red); draw((1,1,0)--(1,1,1),red); draw((1,0,0)--(1,0,1),red); draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle,red); [/asy]

[asy] import three; unitsize(3); currentprojection=orthographic(2*Cos(60),2*Sin(60),1/2); draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle,red); draw((0,0,0)--(0,0,1),red); draw((0,1,0)--(0,1,1),red); draw((1,1,0)--(1,1,1),red); draw((1,0,0)--(1,0,1),red); draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle,red); [/asy]

[asy] import three; unitsize(3); currentprojection=orthographic(2*Cos(75),2*Sin(75),1/2); draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle,red); draw((0,0,0)--(0,0,1),red); draw((0,1,0)--(0,1,1),red); draw((1,1,0)--(1,1,1),red); draw((1,0,0)--(1,0,1),red); draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle,red); [/asy] +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

Circle diagrams

A collection of stuff having to do with circles

Intersection points

Starring: Fancy labels, Troubleshooting

[asy] unitsize(9); pair A1 = (0,0); pair A2 = A1 + dir(0)*30; pair A3 = A2 + dir(0)*30; pair B1 = (9,0); pair B2 = B1 + dir(0)*30; pair B3 = B2 + dir(0)*30; pair G1 = (9/2,-15/2); pair G2 = G1 + dir(0)*30; pair G3 = G2 + dir(0)*30; pair H1 = A1 + dir(90)*5; pair H2 = A2 + dir(90)*5; pair H3 = A3 + dir(90)*5; pair I1 = B1 + dir(90)*3; pair I2 = B2 + dir(90)*4; pair I3 = B3 + dir(90)*5; pair J1 = A1 + dir(120)*5; pair J2 = A2 + dir(120)*5; pair J3 = A3 + dir(120)*5; pair K1 = B1 + dir(60)*3; pair K2 = B2 + dir(60)*4; pair K3 = B3 + dir(60)*5; pair N1 = G1 + dir(270)*3; pair N2 = G2 + dir(270)*3; pair N3 = G3 + dir(270)*3; path E1 = circle(A1,5); path E2 = circle(A2,5); path E3 = circle(A3,5); path F1 = circle(B1,3); path F2 = circle(B2,4); path F3 = circle(B3,5); path L1 = A1--J1; path L2 = A2--J2; path L3 = A3--J3; path M1 = B1--K1; path M2 = B2--K2; path M3 = B3--K3; path O1 = A1--B1; path O2 = A2--B2; path O3 = A3--B3; draw(E1,red); draw(E2,red); draw(E3,red); draw(F1,green); draw(F2,green); draw(F3,green); draw(L1,red); draw(L2,red); draw(L3,red); draw(M1,green); draw(M2,green); draw(M3,green); draw(O1,blue); draw(O2,blue); draw(O3,blue); dot(A1); dot(A2); dot(A3); dot(B1); dot(B2); dot(B3); label("$O_{A1}$",A1,dir(240),red); label("$O_{A2}$",A2,dir(240),red); label("$O_{A3}$",A3,dir(240),red); label("$O_{B1}$",B1,dir(300),green); label("$O_{B2}$",B2,dir(300),green); label("$O_{B3}$",B3,dir(300),green); label("No points",G1); label("One point",G2); label("Two points",G3); label("$r_{A1}+r_{B1}<d_1$",N1); label("$r_{A2}+r_{B2}=d_2$",N2); label("$r_{A3}+r_{B3}>d_3$",N3); label("$r_{A1}$",L1,dir(210),red); label("$r_{A2}$",L2,dir(210),red); label("$r_{A3}$",L3,dir(210),red); label("$r_{B1}$",M1,dir(330),green); label("$r_{B2}$",M2,dir(330),green); label("$r_{B3}$",M3,dir(330),green); label("$d_1$",O1,dir(240),blue); label("$d_2$",O2,dir(240),blue); label("$d_3$",O3,dir(240),blue); pair [] D1 = intersectionpoints(E2,F2); pair [] D2 = intersectionpoints(E3,F3); pair C1 = D1[0]; pair C2 = D2[0]; pair C3 = D2[1]; dot(C1,blue); dot(C2,blue); dot(C3,blue); label("$I_2$",C1,dir(315),blue); label("$I_{3a}$",C2,dir(0),blue); label("$I_{3b}$",C3,dir(0),blue); [/asy] +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

Function $f(x) = 3\tanh (x)+\sin (x)$

Starring: Functions [asy] unitsize(8); pair f(real x1){ real y1 = 3*tanh(x1)+(sin(x1)); pair p1 = (x1,y1); return p1; } pair[] plotpoints = {}; for (int i=0;i<2001;++i){ plotpoints.push(f((i/100)-10)); } for (int i=0;i<2000;++i){ draw(plotpoints[i]--plotpoints[i+1],linewidth(0.5)+blue); } [/asy] +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

Sheet

Starring: Bezier surfaces [asy] import three; currentprojection=orthographic(1,1,5); size(200); pair[] l1x={(-2,0), (-1.3,0.5), (-0.7,0.5), (0,0)}; pair[] l1y={(-2,0), (-1.3,0.5), (-0.7,0.5), (0,0)}; triple f1(int xp, int yp) { real Z = l1x[xp].y + l1y[yp].y; real X = l1x[xp].x; real Y = l1y[yp].x; triple pt = (X,Y,Z); return pt; }; triple[][] P1={{},{},{},{}}; for (int i=0;i<4;++i){ for (int j=0; j<4;++j){ triple[] temp = P1[i]; temp.push(f1(i,j)); P1.delete(i); P1.insert(i,temp); } } for (int i=0;i<4;++i){ for (int j=0; j<4;++j){ dot(P1[i][j]); } } draw(surface(patch(P1,new pen[]{cyan,cyan+green,cyan+yellow+green+red,cyan+yellow}))); pair[] l2x={(-2,0), (-1.3,0.5), (-0.7,0.5), (0,0)}; pair[] l2y={(0,0), (0.7,-0.5), (1.3,-0.5), (2,0)}; triple f2(int xp, int yp) { real Z = l2x[xp].y + l2y[yp].y; real X = l2x[xp].x; real Y = l2y[yp].x; triple pt = (X,Y,Z); return pt; }; triple[][] P2={{},{},{},{}}; for (int i=0;i<4;++i){ for (int j=0; j<4;++j){ triple[] temp = P2[i]; temp.push(f2(i,j)); P1.delete(i); P1.insert(i,temp); } } for (int i=0;i<4;++i){ for (int j=0; j<4;++j){ dot(P2[i][j]); } } draw(surface(patch(P2,new pen[]{cyan+yellow,cyan+yellow+green+red,yellow+red,yellow}))); pair[] l3x={(0,0), (0.7,-0.5), (1.3,-0.5), (2,0)}; pair[] l3y={(-2,0), (-1.3,0.5), (-0.7,0.5), (0,0)}; triple f3(int xp, int yp) { real Z = l3x[xp].y + l3y[yp].y; real X = l3x[xp].x; real Y = l3y[yp].x; triple pt = (X,Y,Z); return pt; }; triple[][] P3={{},{},{},{}}; for (int i=0;i<4;++i){ for (int j=0; j<4;++j){ triple[] temp = P3[i]; temp.push(f3(i,j)); P3.delete(i); P3.insert(i,temp); } } for (int i=0;i<4;++i){ for (int j=0; j<4;++j){ dot(P3[i][j]); } } draw(surface(patch(P3,new pen[]{cyan+green,green,green+red,cyan+yellow+green+red}))); pair[] l4x={(0,0), (0.7,-0.5), (1.3,-0.5), (2,0)}; pair[] l4y={(0,0), (0.7,-0.5), (1.3,-0.5), (2,0)}; triple f4(int xp, int yp) { real Z = l4x[xp].y + l4y[yp].y; real X = l4x[xp].x; real Y = l4y[yp].x; triple pt = (X,Y,Z); return pt; }; triple[][] P4={{},{},{},{}}; for (int i=0;i<4;++i){ for (int j=0; j<4;++j){ triple[] temp = P4[i]; temp.push(f4(i,j)); P4.delete(i); P4.insert(i,temp); } } for (int i=0;i<4;++i){ for (int j=0; j<4;++j){ dot(P4[i][j]); } } draw(surface(patch(P4,new pen[]{cyan+yellow+green+red,green+red,red,yellow+red}))); import settings; leftbutton=new string[] {"rotate","zoom","shift","pan"}; middlebutton=new string[] {"menu"}; rightbutton=new string[] {"zoom/menu","rotateX","rotateY","rotateZ"}; wheelup=new string[] {"zoomin"}; wheeldown=new string[] {"zoomout"}; [/asy] +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

Another cube

Starring: Knowledge* [asy] unitsize(72); pen drawing = red; // change it! real rxy = acos(1/1.5*sqrt(2)); real ryz = acos(1/sqrt(3)); real[] unitx = {cos(rxy),-sin(rxy)*cos(ryz),sin(rxy)*sin(ryz)}; real[] unity = {sin(rxy),cos(rxy)*cos(ryz),-cos(rxy)*sin(ryz)}; real[] unitz = {0,sin(ryz),cos(ryz)}; real[][] base = {unitx,unity,unitz}; pair proj(real[] coor){ pair ortho(real[] coor){ pair p=(coor[0],coor[1]); return p; } pair perspec(real[] coor){ real[] center = {0,0,0}; // Write the projection center above real d = (coor[0]-center[0])**2+(coor[1]-center[1])**2+(coor[2]-center[2])**2; pair p=(coor[0]/d,coor[1]/d); return p; } pair p = ortho(coor); // Choose your projection above return p; } real[] newp(real[] s,real[][] base){ real[] ad(real[] in1,real[] in2,real[] in3){ real[] out = {in1[0]+in2[0]+in3[0],in1[1]+in2[1]+in3[1],in1[2]+in2[2]+in3[2]}; return out; } real[] mul(real fac,real[] in){ real[] out = {fac*in[0],fac*in[1],fac*in[2]}; return out; } real[] out = ad(mul(s[0],base[0]),mul(s[1],base[1]),mul(s[2],base[2])); return out; } for (real i=0;i<2;++i){ for (real j=0;j<2;++j){ for (real k=0;k<2;++k){ real[] Orig = {i,j,k}; real[] Ivar = {1-i,j,k}; real[] Jvar = {i,1-j,k}; real[] Kvar = {i,j,1-k}; pair orig = proj(newp(Orig,base)); pair ivar = proj(newp(Ivar,base)); pair jvar = proj(newp(Jvar,base)); pair kvar = proj(newp(Kvar,base)); draw(orig--ivar,drawing); draw(orig--jvar,drawing); draw(orig--kvar,drawing); } } } [/asy] 

* How to put everything together in a nice example, why the only good thing about asymptote three is bezier surfaces. If you're bored, look at the code and try to figure out how it all works.

Created files

(Using desmos)

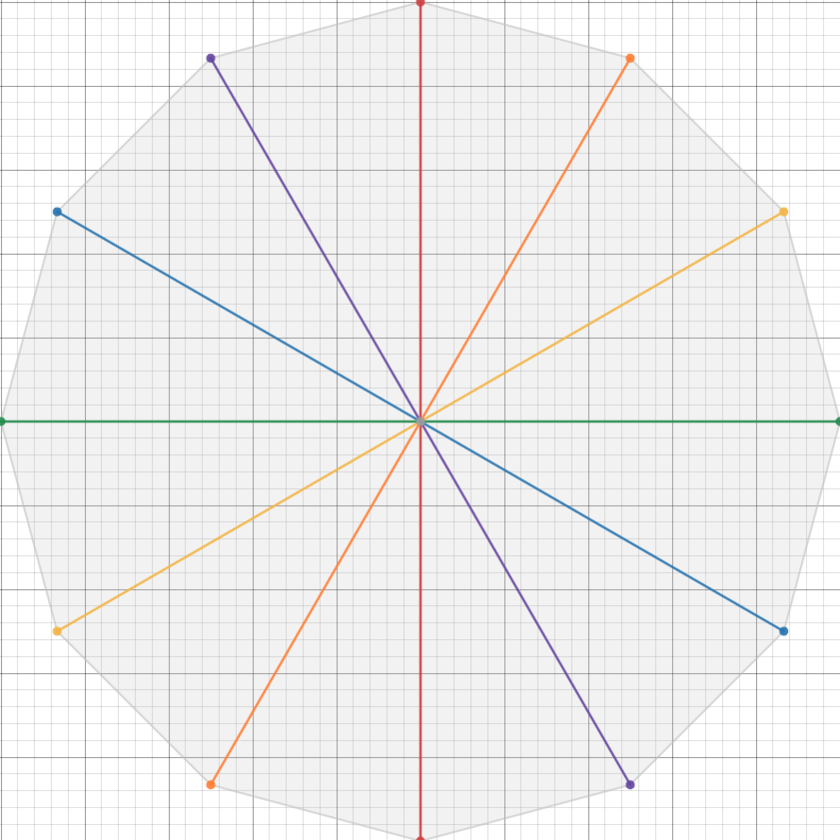
Colored dodecagon

Original file:

Colored dodecagon.png






























File

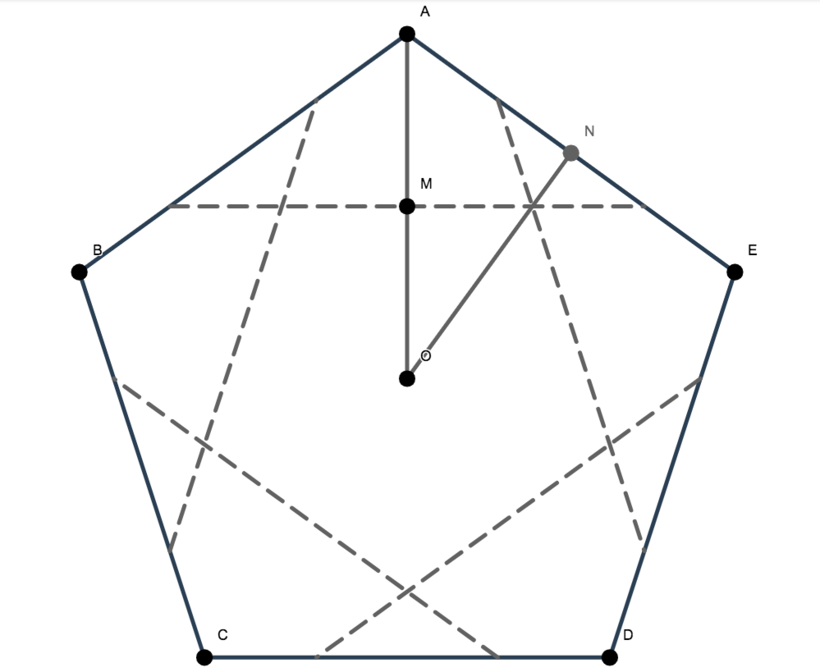
Pentagon 2023 12B Q25 dissmo

Original size:

Pentagon 2023 12B Q25 dissmo.png
























File

LaTeX Creations (coming soon!)

Created pages

Solutions created

2019 AIME II #4 Solution 7 (Generating functions)

[Actual solution]

Let's look at the prime factorization of some of these rolls: 

 01 => 2^0*3^0*5^0
 02 => 2^1*3^0*5^0
 03 => 2^0*3^1*5^0
 04 => 2^2*3^0*5^0
 05 => 2^0*3^0*5^1
 06 => 2^1*3^1*5^0

Now, using multi-variable generating functions, we get: 

 f(x,y,z)=1+x+y+x^2+z+xy
            | |
           \| |/
            'v'
 f(x,y,z)=1+x+y+z+x^2+xy
   =(for our purposes)
       =2+x+y+z+xy

Let's square that! 

 4+2x+2y+2z+2xy+2x+x^2+xy+xz+x^2y+2y+xy+y^2+yz+xy^2+2z+xz+yz+z^2+xyz+2xy+x^2y+xy^2+xyz+x^2y^2
 Combining like terms . . .
 4+4x+4y+4z+x^2+y^2+z^2+6xy+2xz+2yz+2xyz+2x^2y+2xy^2+x^2y^2

Since we only want the parity of each of the exponents, we can collapse it again. 

 8+6x+6y+4z+6xy+2xz+2yz+2xyz

Last simplification: factor out a factor of two and save it for later. 

 4+3x+3y+2z+3xy+xz+yz+xyz

Let's take a better approach this time. 

 ___ term :4*4+3*3+3*3+2*2+3*3+1*1+1*1+1*1=16+09+09+04+09+01+01+01=50
 __x term :4*3+3*4+3*3+2*1+3*3+1*2+1*1+1*1=12+12+09+02+09+02+01+01=48
 __y term :4*3+3*3+3*4+2*1+3*3+1*1+1*2+1*1=12+09+12+02+09+01+02+01=48
 __z term :4*2+3*1+3*1+2*4+3*1+1*3+1*3+1*3=08+03+03+08+03+03+03+03=34
 _xy term :4*3+3*3+3*3+2*1+3*4+1*1+1*1+1*2=12+09+09+02+12+01+01+02=48
 _xz term :4*1+3*2+3*1+2*3+3*1+1*4+1*3+1*3=04+06+03+06+03+04+03+03=32
 _yz term :4*1+3*1+3*2+2*3+3*1+1*3+1*4+1*3=04+03+06+06+03+03+04+03=32
 xyz term :4*1+3*1+3*1+2*3+3*2+1*3+1*3+1+4=04+03+03+06+06+03+03+04=32
 
 Result: 50+48x+48y+34z+48xy+32xz+32yz+32xyz

I know we could use vectors and dot products to make it look neater but come on. It already looks neat enough. Also, we didn't need the other parts, but it just looks nicer. Now let's stick back the two that turned into a four. 

 200+192x+192y+136z+192xy+128xz+128yz+128xyz

We seek the constant term which is 200. 200/1296=100/648=50/324=25/162, 25+162=187

Yrock's Notes

hello

ConfidentFlamingo's notes

Other Users' notes

Note from afly: If you leave a note, write who it is from

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=User:Afly&oldid=230191"