Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "User:Fura3334"
 
(10 intermediate revisions by the same user not shown)
Line 1: Line 1:
 
IF YOU'RE AN ADMIN, PLS DONT DELETE THIS PAGE, IM WORKING ON SUS MOCK AIME (well, if i haven't edited this page for 2 weeks, you can delete it)
 
IF YOU'RE AN ADMIN, PLS DONT DELETE THIS PAGE, IM WORKING ON SUS MOCK AIME (well, if i haven't edited this page for 2 weeks, you can delete it)
  
−
[hide="the 6 problems for sus mock aime, now in latex"]
+
==Problem 1==
−
[b]Problem 1[/b]
 
 
Kube the robot completes a task repeatedly, each time taking <math>t</math> minutes. One day, Furaken asks Kube to complete <math>n</math> identical tasks in <math>20</math> hours. If Kube works slower and spends <math>t+6</math> minutes on each task, it will finish <math>n</math> tasks in exactly <math>20</math> hours. If Kube works faster and spends <math>t-6</math> minutes on each task, it can finish <math>n+1</math> tasks in <math>20</math> hours with <math>12</math> minutes to spare. Find <math>t</math>.
 
Kube the robot completes a task repeatedly, each time taking <math>t</math> minutes. One day, Furaken asks Kube to complete <math>n</math> identical tasks in <math>20</math> hours. If Kube works slower and spends <math>t+6</math> minutes on each task, it will finish <math>n</math> tasks in exactly <math>20</math> hours. If Kube works faster and spends <math>t-6</math> minutes on each task, it can finish <math>n+1</math> tasks in <math>20</math> hours with <math>12</math> minutes to spare. Find <math>t</math>.
−
Answer: [hide]i'm not putting the answer here, send your answer in this thread then i'll see whether yours is same as mine[/hide]
 
  
−
[b]Problem 2[/b]
+
==Problem 2==
 
Let <math>x</math>, <math>y</math>, <math>z</math> be positive real numbers such that
 
Let <math>x</math>, <math>y</math>, <math>z</math> be positive real numbers such that
−
<math>xz = 1000</math>
+
* <math>xz = 1000</math>
−
<math>z = 100\sqrt{xy}</math>
+
* <math>z = 100\sqrt{xy}</math>
−
<math>10^{\lg x\lg y + 2\lg y\lg z + 3\lg z\lg x} = 2 \cdot 5^{12}</math>
+
* <math>10^{\lg x\lg y + 2\lg y\lg z + 3\lg z\lg x} = 2 \cdot 5^{12}</math>
 
Find <math>\lfloor x+y+z \rfloor</math>.
 
Find <math>\lfloor x+y+z \rfloor</math>.
−
Answer: [hide]i'm not putting the answer here, send your answer in this thread then i'll see whether yours is same as mine[/hide]
 
  
−
[b]Problem 3[/b]
+
==Problem 3==
−
Let <math>p</math> be an odd prime such that <math>2^{p-7}\equiv3 \pmod{p}</math>. Find <math>p</math>.
+
 
−
Answer: [hide]i'm not putting the answer here, send your answer in this thread then i'll see whether yours is same as mine[/hide]
+
 
 +
==Problem 4==
 +
[[File:susmockaimep4diagram.png|252px|center]]
  
−
[b]Problem 4[/b]
 
−
[img]https://latex.artofproblemsolving.com/d/4/4/d44b620826b6207a9018efd4b6db89b39b2b9b3c.png[/img]
 
 
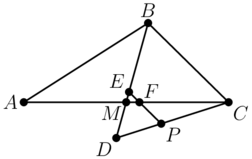
For triangle <math>ABC</math>, let <math>M</math> be the midpoint of <math>AC</math>. Extend <math>BM</math> to <math>D</math> such that <math>MD=2.8</math>. Let <math>E</math> be the point on <math>MB</math> such that <math>ME=0.8</math>, and let <math>F</math> be the point on <math>MC</math> such that <math>MF=1</math>. Line <math>EF</math> intersects line <math>CD</math> at <math>P</math> such that <math>\tfrac{DP}{PC}=\tfrac23</math>. Given that <math>EF</math> is parallel to <math>BC</math>, the maximum possible area of triangle <math>ABC</math> can be written as <math>\tfrac{p}{q}</math> where <math>p</math> and <math>q</math> are relatively prime positive integers. Find <math>p+q</math>.
 
For triangle <math>ABC</math>, let <math>M</math> be the midpoint of <math>AC</math>. Extend <math>BM</math> to <math>D</math> such that <math>MD=2.8</math>. Let <math>E</math> be the point on <math>MB</math> such that <math>ME=0.8</math>, and let <math>F</math> be the point on <math>MC</math> such that <math>MF=1</math>. Line <math>EF</math> intersects line <math>CD</math> at <math>P</math> such that <math>\tfrac{DP}{PC}=\tfrac23</math>. Given that <math>EF</math> is parallel to <math>BC</math>, the maximum possible area of triangle <math>ABC</math> can be written as <math>\tfrac{p}{q}</math> where <math>p</math> and <math>q</math> are relatively prime positive integers. Find <math>p+q</math>.
−
Answer: [hide]i'm not putting the answer here, send your answer in this thread then i'll see whether yours is same as mine[/hide]
 
  
−
[b]Problem 5[/b]
+
==Problem 5==
 
Let <math>1 + \sqrt3 + \sqrt{13}</math> be a root of the polynomial <math>x^4 + ax^3 + bx^2 + cx + d</math> where <math>a</math>, <math>b</math>, <math>c</math>, <math>d</math> are integers. Find <math>d</math>.
 
Let <math>1 + \sqrt3 + \sqrt{13}</math> be a root of the polynomial <math>x^4 + ax^3 + bx^2 + cx + d</math> where <math>a</math>, <math>b</math>, <math>c</math>, <math>d</math> are integers. Find <math>d</math>.
−
Answer: [hide]i'm not putting the answer here, send your answer in this thread then i'll see whether yours is same as mine[/hide]
 
  
−
[b]Problem 6[/b]
+
==Problem 6==
−
[img]https://latex.artofproblemsolving.com/4/6/1/461d152569bf18e1c406d5b3c3a3afa4201b4245.png[/img]
+
[[File:susmockaimep6diagram.png|252px|center]]
 
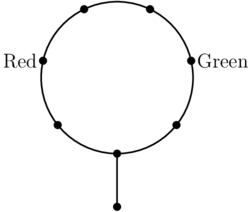
Fly has a large number of red, yellow, green and blue pearls. Fly is making a necklace consisting of <math>8</math> pearls as shown in the diagram. One slot already has a red pearl, and another slot has a green pearl. Find the number of ways to fill the <math>6</math> remaining slots such that any two pearls that are connected directly have different colors.
 
Fly has a large number of red, yellow, green and blue pearls. Fly is making a necklace consisting of <math>8</math> pearls as shown in the diagram. One slot already has a red pearl, and another slot has a green pearl. Find the number of ways to fill the <math>6</math> remaining slots such that any two pearls that are connected directly have different colors.
−
Answer: [hide]i'm not putting the answer here, send your answer in this thread then i'll see whether yours is same as mine[/hide][/hide]
+
 
 +
==Problem X==
 +
(I haven't decided the problem number yet)
 +
 
 +
Let <math>N=109007732774081</math>. Given that <math>N=pq</math> where <math>p</math>, <math>q</math> are distinct primes greater than <math>1000</math>, and that <math>N</math> cannot be expressed as the sum of 2 perfect squares, find the remainder when
 +
<cmath>\frac{\varphi(N)^2}{2} - (\varphi(N)+1)^6</cmath>
 +
is divided by 144.

Latest revision as of 23:49, 14 March 2024

IF YOU'RE AN ADMIN, PLS DONT DELETE THIS PAGE, IM WORKING ON SUS MOCK AIME (well, if i haven't edited this page for 2 weeks, you can delete it)

Problem 1

Kube the robot completes a task repeatedly, each time taking $t$ minutes. One day, Furaken asks Kube to complete $n$ identical tasks in $20$ hours. If Kube works slower and spends $t+6$ minutes on each task, it will finish $n$ tasks in exactly $20$ hours. If Kube works faster and spends $t-6$ minutes on each task, it can finish $n+1$ tasks in $20$ hours with $12$ minutes to spare. Find $t$.

Problem 2

Let $x$, $y$, $z$ be positive real numbers such that

  • $xz = 1000$
  • $z = 100\sqrt{xy}$
  • $10^{\lg x\lg y + 2\lg y\lg z + 3\lg z\lg x} = 2 \cdot 5^{12}$

Find $\lfloor x+y+z \rfloor$.

Problem 3

Problem 4

Susmockaimep4diagram.png

For triangle $ABC$, let $M$ be the midpoint of $AC$. Extend $BM$ to $D$ such that $MD=2.8$. Let $E$ be the point on $MB$ such that $ME=0.8$, and let $F$ be the point on $MC$ such that $MF=1$. Line $EF$ intersects line $CD$ at $P$ such that $\tfrac{DP}{PC}=\tfrac23$. Given that $EF$ is parallel to $BC$, the maximum possible area of triangle $ABC$ can be written as $\tfrac{p}{q}$ where $p$ and $q$ are relatively prime positive integers. Find $p+q$.

Problem 5

Let $1 + \sqrt3 + \sqrt{13}$ be a root of the polynomial $x^4 + ax^3 + bx^2 + cx + d$ where $a$, $b$, $c$, $d$ are integers. Find $d$.

Problem 6

Susmockaimep6diagram.png

Fly has a large number of red, yellow, green and blue pearls. Fly is making a necklace consisting of $8$ pearls as shown in the diagram. One slot already has a red pearl, and another slot has a green pearl. Find the number of ways to fill the $6$ remaining slots such that any two pearls that are connected directly have different colors.

Problem X

(I haven't decided the problem number yet)

Let $N=109007732774081$. Given that $N=pq$ where $p$, $q$ are distinct primes greater than $1000$, and that $N$ cannot be expressed as the sum of 2 perfect squares, find the remainder when \[\frac{\varphi(N)^2}{2} - (\varphi(N)+1)^6\] is divided by 144.

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=User:Fura3334&oldid=216991"